Answered step by step
Verified Expert Solution
Question
1 Approved Answer
I have 3 questions, based on the attachment below: Explain how the term underlined by BLUE is obtained Does the statement underlined by RED, refer
I have 3 questions, based on the attachment below:
- Explain how the term underlined by BLUE is obtained
- Does the statement underlined by RED, refer to the statement "but that these partials are not continuous at (0,0)". Please explain in more detail
- Please explain in detail, the GREEN box
Please explain clearly showing each step as thoroughly as possible.
If you are using hand-written notes, then please ensure they are tidy and legible as untidy written notes are difficult to interpret.
Alternatively use LaTeX.
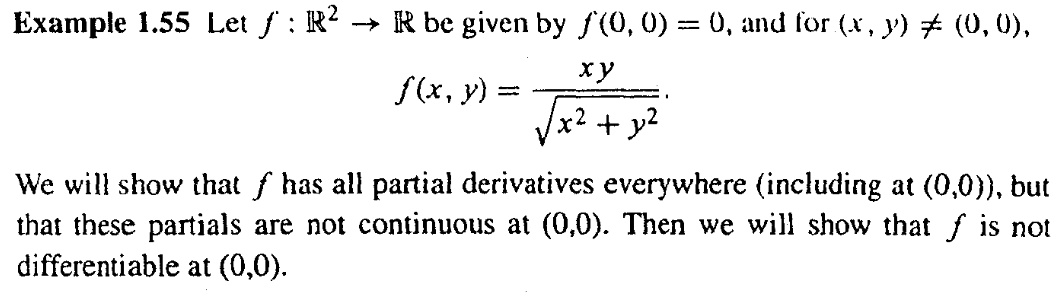

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


