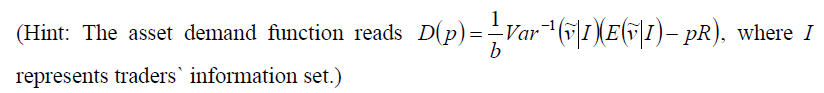I have a question in statistics regarding jointly normally and independantly distributed random variables:

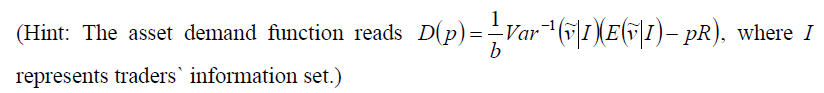
The supply function is just constant and donated with Z. b is the parameter of absolute risk aversion. Furthermore d = v

Consider a two-period economy and two strictly isolated islands i = A, B. There is neither travel nor trade across islands. But N investors i country A and NB in country B can buy a non-perishable real asset called gold. Gold serves as a numeraire and, hence, is traded at the price 1 in both periods. A stock market is active on each island for daily trading. The stock index is trading at p; for i = A,B in t = 0. The aggregate dividends on an index certificate in country i are denoted by d; and are paid out in period t = 2 in terms of units of gold. Aggregate supply of the stock index is normalized to in each country. Investors in country A are risk averse with constant absolute risk aversion of 1, while they are risk neutral in country B. The dividend generating processes in country i are d = A + B + , where the country factors fi~ N(, 07) and the country-specific error terms ; ~ N(0, t7) are jointly normally and independantly distributed. (Hint: The asset demand function reads represents traders` information set.) D(p) = Var(~^|1)(E(~|I) pR), where I a. At which price does the index trade in each country i when no further information is available to investors? Explain carefully. b. Now assume that in each island i a proportion is informed about the realization of the local factor realization f;. Which price will obtain now? Assume that only prices in the own island can be observed. Explain carefully. c. How does the amount of informed traders affect the market risk premium in question b relative to the case of no information? What happens, if unformed traders can only observe the prices in the other islands? Consider a two-period economy and two strictly isolated islands i = A, B. There is neither travel nor trade across islands. But N investors i country A and NB in country B can buy a non-perishable real asset called gold. Gold serves as a numeraire and, hence, is traded at the price 1 in both periods. A stock market is active on each island for daily trading. The stock index is trading at p; for i = A,B in t = 0. The aggregate dividends on an index certificate in country i are denoted by d; and are paid out in period t = 2 in terms of units of gold. Aggregate supply of the stock index is normalized to in each country. Investors in country A are risk averse with constant absolute risk aversion of 1, while they are risk neutral in country B. The dividend generating processes in country i are d = A + B + , where the country factors fi~ N(, 07) and the country-specific error terms ; ~ N(0, t7) are jointly normally and independantly distributed. (Hint: The asset demand function reads represents traders` information set.) D(p) = Var(~^|1)(E(~|I) pR), where I a. At which price does the index trade in each country i when no further information is available to investors? Explain carefully. b. Now assume that in each island i a proportion is informed about the realization of the local factor realization f;. Which price will obtain now? Assume that only prices in the own island can be observed. Explain carefully. c. How does the amount of informed traders affect the market risk premium in question b relative to the case of no information? What happens, if unformed traders can only observe the prices in the other islands