Question: I have assignment for Geological computational using Jupyter notebook which is coding. I need someone who is geologist and have experience with Jupyter notebook for
I have assignment for Geological computational using Jupyter notebook which is coding. I need someone who is geologist and have experience with Jupyter notebook for coding. the assignment is about math on maps. it is about find the coordinates of locations on the map. also, the assignment is about 3 examples and each example have parts of questions.

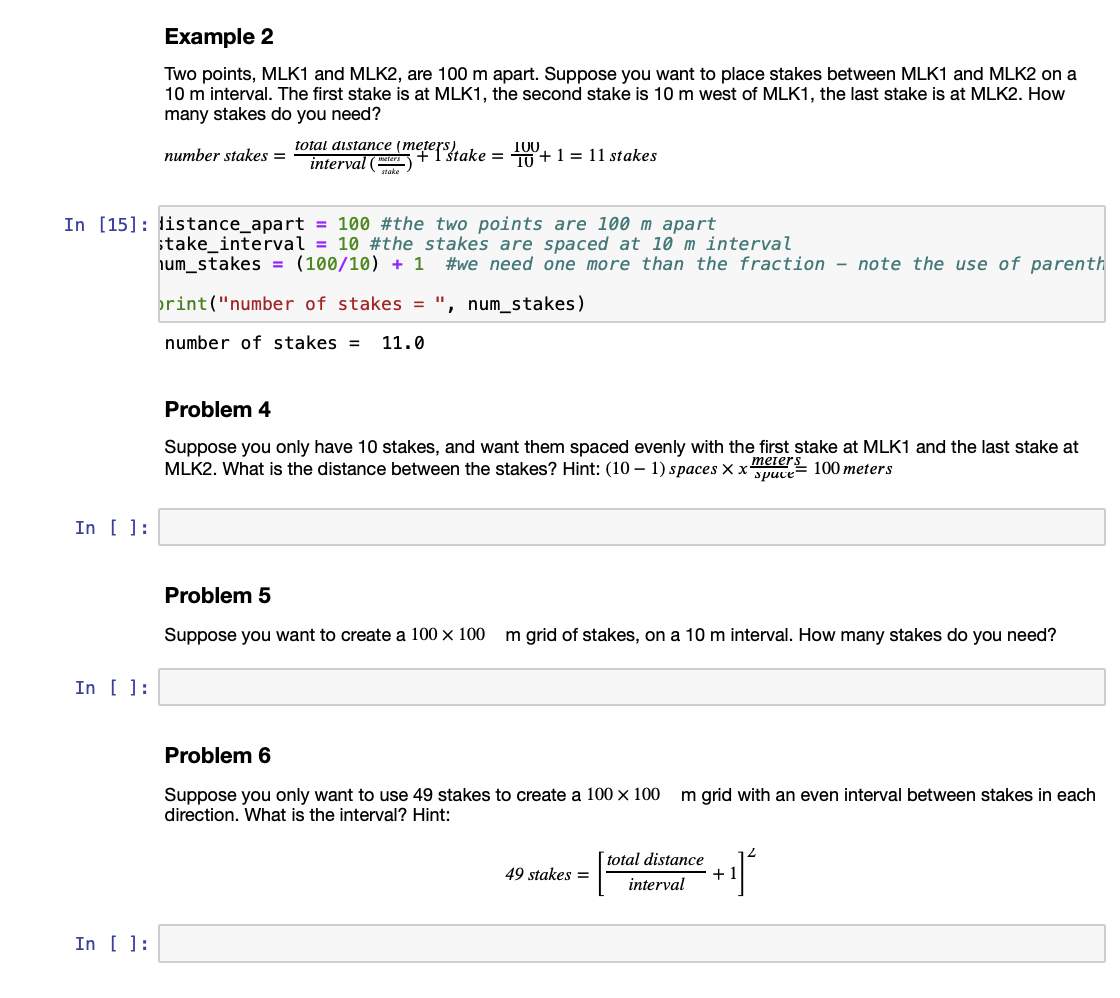




Problem Set 1 This problem set involves solving problems related to map coordinates. Read the background and study the examples. Write your answer in the cells provided by writing the solution using python code. Be sure that your answer prints out using the format shown in examples. Print the solution in words, give the value, and give the value's units. Save your workbook (frequently!). When you save your notbook, save as "yourname-Notebook1", and turn in your notebook by uploading it on canvas. Background Rectangular grid systems are widely used by geoscientists to simplify distance calculations on maps. These are Cartesian grids. The Y-axis is oriented N-S and Y-coordinates are usually referred to as the Northing, or sometimes as distance north. The X-axis is oriented E-W and X coordinates are referred to as the Easting or distance east. Usually the units of these grids are meters. The most important grid in use today is the Universal Transverse Mercator (UTM) grid. The Northing for the UTM grid in the northern hemisphere is given in meters north of the equator. Negative numbers are avoided at all costs in the UTM grid. So, in the southern hemisphere, the Northing is given in meters south of the equator (a negative number) + 10,000,000 m. For example, the Northing of a point located 2000 km north of the equator is 2,000,000 N. The Northing of a point located 2000 km south of the equator is 8,000,000, N. In both the northern and southern hemispheres, UTM Northing is a positive number that increases as one walks north and decreases as one walks south. The X-axis is perpendicular to the Y-axis at the origin (central meridian) of the coordinate system. Far from the central meridian, this results in considerable distortion of the grid. Consequently, the UTM grid breaks up the Earth's surface into 60 zones, each with its own central meridian. Again, negative numbers are avoided in the UTM grid. Consequently the value of the Easting along the central meridian (the origin) of any zone is 500,000 E, rather than 0 E. West of the central meridian the Easting is less than 500,000 E; east of the central the Easting is more than 500,000 E. There are enough zones so that, using this scheme, no negative Easting coordinates occur on Earth. When UTM coordinates are used, the zone must be reported. These zones are uniquely numbered 1--60. It is also necessary to specify if the coordinate in the zone is in the northern hemisphere (N), or the southern hemisphere (S). For example, the University of South Florida campus is in zone 17 N. Within this zone the SCA building has the approximately UTM coordinates: 3104700 360830 E. The SCA building is about 3,104.7 km north of the equator. Example 1 Suppose a GPS gives the coordinate of a point in the MLK Plaza (MLK1) on the USF campus to be 3104941 N, 360912 E. How far north of the coordinate of the SCA building is MLK1? In [14] : mlk1_north = 3104941 #assign a variable to MLK1 northing sca_north = 3104700 #assign a variable to SCA northing distance_north = mki_north - sca_north #difference the value print("distance = ", distance_north, "m") #print the answer distance = 241 m Problem 1 - solve with a python script How far East of the coordinate of the SCA building is MLK1? Hint. Follow the same procedure as given in example #1 In [ ]: Problem 2 What is the coordinate of a point 100 m west of the MLK Plaza point (MLK2)? In [ ]: Problem 3 What is the UTM coordinate of a point located in zone 17, 100 m west of the central meridian and 130 m south of the equator? Hint, remember that the northing coordinate of the equator is 10,000,000 m, for points located in the southern hemisphere. Also remember that the easting coordinate of any central meridian (there are 60!) is 500,000 E. In (): Problem 4 A USF MS student, John Petriello, did a GPR survey on deposits from Puluagua volcano, Ecuador. The deposits, and John's survey line, crossed the equator. This created an offset in the northing coordinates along John's line at the equator. To solve this problem, John created a local grid using the UTM coordinates of the southern hemuisphere even for points located along the survey line in the northern hemisphere. That is, in John's local grid, a point located 100 m north of the equator would have the northing coordinate 10000100 N, which is not an allowable UTM coordinate but is a fine value for the local grid. Unfortunately, John's GPS report locations in UTM coordinates, not in his local grid coordinates. The coordinates of the beginning and end points along John's survey line, in real UTM coordinates, are: First Point: 9999564,N, 785342, E zone 17, S Second Point 265 N, 785358 E zone 17, N Convert to these coordinates to John's local grid. In ( ): Background Often geoscientists want to make measurements along a line at even intervals, or on a map grid at even intervals. Example measurements made at even intervals might be the dip of a geologic bed, the depth to the water table, or the variation in the Earth's gravity. A schema: Beware that the measured interval is one less than the number of counts, unless the first count is zero. If you have N equally spaced stakes in the ground, there are N - 1 intervals between the stakes. Example 2 Two points, MLK1 and MLK2, are 100 m apart. Suppose you want to place stakes between MLK1 and MLK2 on a 10 m interval. The first stake is at MLK1, the second stake is 10 m west of MLK1, the last stake is at MLK2. How many stakes do you need? meters) number stakes = interval ( Cheerftake = 100+1 = 11 stakes stake In [15] : listance_apart = 100 #the two points are 100 m apart take_interval = 10 #the stakes are spaced at 10 m interval num_stakes = (100/10) + 1 #we need one more than the fraction - note the use of parenth brint("number of stakes = " , num_stakes) number of stakes = 11.0 Problem 4 Suppose you only have 10 stakes, and want them spaced evenly with the first stake at MLK1 and the last stake at MLK2. What is the distance between the stakes? Hint: (10 1) spaces x x spuce meter: 100 meters In [ ]: Problem 5 Suppose you want to create a 100 x 100 m grid of stakes, on a 10 m interval. How many stakes do you need? In [ ]: Problem 6 Suppose you only want to use 49 stakes to create a 100 x 100 direction. What is the interval? Hint: m grid with an even interval between stakes in each total distance 49 stakes = interval In [ ]: Problem 7 A satellite maps topography along a 2400 km-long transect in a N--S direction across North America. The satellite data are processed to provide one elevation measurement every 30 m of horizontal distance along the transect. How many elevation measurements are in the transect? In [ ]: Problem 8 A digital elevation model (DEM) is a map grid of elevation measurements. Usually, one axis of the grid runs N--S and the other axis runs E--W. If the southwesternmost corner of the DEM is located at 3200104 N, 500000 E, the spacing between elevation measurements in the grid is 30 m in both directions, and there are a total of 200 measurements in each direction, what is the UTM coordinate of the NE corner of the DEM? In [ ]: Background Originally the meter was intended to be defined in terms of the distance from the equator to the pole. Specifically, it was thought this distance is 10,000 kilometers. It turns out this is not exactly right, because the Earth is not quite spherical, and because at the time the meter was defined the distance between pole and equator was not precisely known. Nevertheless, it's close. To answer these questions, assume that the distance from the equator to the north pole is 10,000 kilometers and that the Earth is a perfect sphere. Problem 9 How many meters is it from the south pole to the equator? Hint: This is a question about unit conversion from kilometers to meters. In [ ]: Problem 10 Calculate the circumference of the Earth in kilometers. In [ ]: Example 3 Calculate the radius of the Earth. Recall that the circumference of a circle is 2nr , wherer is the radius. In [16]: #in order to use the value of PI and a lot of other math #import this module import math circumferance = 40000 #kilometers, right? #solve for radius #note pi is math.pi (because it is a feature of the math module) # note () in denominator to solve this equation correctly. radius = circumferance/(2*math.pi) print ("radius = ", radius, "km") radius = 6366.197723675814 km Problem 11 Since there are 60 UTM zones, what is the maximum width of a zone at the equator (in meters)? In ( ): Problem 12 Since the central meridian of a UTM zone is 500000 E, what are the maximum and minimum UTM Easting coordinates you would expect to find in any zone at the equator? In [ ]: Problem 13 The depth to the outer core is about 2900 km. What is the circumference of the Earth's outer core? In [ ]: Background A sphere has constant radius and the Earth does not. The equatorial radius of the Earth is approximately 6378.137 km, the polar radius of the Earth is approximately 6356.752 km. Consequently, the figure of the Earth is more precisely approximated by an oblate ellipsoid of revolution. The planet is flattened along its axis of rotation, its equatorial bulge a result of rotation. The Earth is wider around its waistline (the equator) than around the poles. The amount of flattening of the ellipsoid can be expressed in terms of equatorial and polar radii: Reg-Rpo f = Req equatorial and polar radii: Req- Rpo Req where Req is the radius of the Earth at the equator and Rpo is the radius at the pole. The magnitude of flattening, f , is now very well determined from observing artificial satellite orbits around the Earth, and is fixed for the WGS84 ellipsoid as f = 1/298.257223563 . Newton first discussed the flattening of the Earth, and estimated a value of 1/230. The radius of the Earth at a given latitude is given by RE= Reg 1 - fsinfo) where: RE is the Earth's radius at latitude , Req is the radius of the Earth at the equator, approximately 6378137 m, and f is the flattening. Problem 14 Based on height above sealevel, Mt. Everest (8,848 m above sealevel, about 28 degrees N) is the highest place on Earth. Cotopaxi volcano (5,897 m above sealevel, about 1 degree N) is also a very high mountain. What if we measured height with respect to the center of the Earth? Which is taller: Cotopaxi or Everest? Hint: For distance from the center of the Earth of Mt Everest: = 6378.137(1 - (1/298.257) sin 28) + 8.848 = 6382.272 km In [18] : this bit of code solves the hint you have to write the rest of the code to solve this problem! import the math module mport math specify earth parameters quatorial_radius = 6378.137 #kilometers lattening = 1/298.257 info needed about Mt. Everest atitude_mt_everest = 28 #degrees eight_mt_everest = 8.848 #kilometers step 1 - convert latitude to radians python does caluclations in radians adians_mt_everest = 28 * math.pi/180 step 2 - find distance of the top of Mt Everest from center of earth listance_mt_everest = equatorial_radius*(1-flattening*math.sin(radians_mt_everest)**2) + rint ("distance of Mt Everest from earth center = ", distance_mt_everest, "km") now complete the code making the same calculation for Cotopaxi and compare the results distance of Mt Everest from earth center = 6382.271735848219 km Background Latitude and longitude can be expressed in decimal degrees (for example, MLK1:28.0626 N, 82.4153 W) or in degrees, minutes and seconds. To convert 28.0626 N to degrees and minutes, express the latitude with a whole number and a remainder. The remainder is multiplied by 60, because there are 60 minutes in 1 degree. 28.0626 N = 28 + 0.0626 x 60 minutes/degree = 28 3.756' To convert to degrees, minutes, and seconds the minutes must be treated as a whole number and remainder that is multiplied by 60, because there are 60 seconds in one minute. 28 3.756' N = 28 + 3 +0.756' x 60 seconds/minute = 283'45.36" N Problem 15 Convert the longitude 82.4153 W to degrees minutes seconds In [ ]: Problem Set 1 This problem set involves solving problems related to map coordinates. Read the background and study the examples. Write your answer in the cells provided by writing the solution using python code. Be sure that your answer prints out using the format shown in examples. Print the solution in words, give the value, and give the value's units. Save your workbook (frequently!). When you save your notbook, save as "yourname-Notebook1", and turn in your notebook by uploading it on canvas. Background Rectangular grid systems are widely used by geoscientists to simplify distance calculations on maps. These are Cartesian grids. The Y-axis is oriented N-S and Y-coordinates are usually referred to as the Northing, or sometimes as distance north. The X-axis is oriented E-W and X coordinates are referred to as the Easting or distance east. Usually the units of these grids are meters. The most important grid in use today is the Universal Transverse Mercator (UTM) grid. The Northing for the UTM grid in the northern hemisphere is given in meters north of the equator. Negative numbers are avoided at all costs in the UTM grid. So, in the southern hemisphere, the Northing is given in meters south of the equator (a negative number) + 10,000,000 m. For example, the Northing of a point located 2000 km north of the equator is 2,000,000 N. The Northing of a point located 2000 km south of the equator is 8,000,000, N. In both the northern and southern hemispheres, UTM Northing is a positive number that increases as one walks north and decreases as one walks south. The X-axis is perpendicular to the Y-axis at the origin (central meridian) of the coordinate system. Far from the central meridian, this results in considerable distortion of the grid. Consequently, the UTM grid breaks up the Earth's surface into 60 zones, each with its own central meridian. Again, negative numbers are avoided in the UTM grid. Consequently the value of the Easting along the central meridian (the origin) of any zone is 500,000 E, rather than 0 E. West of the central meridian the Easting is less than 500,000 E; east of the central the Easting is more than 500,000 E. There are enough zones so that, using this scheme, no negative Easting coordinates occur on Earth. When UTM coordinates are used, the zone must be reported. These zones are uniquely numbered 1--60. It is also necessary to specify if the coordinate in the zone is in the northern hemisphere (N), or the southern hemisphere (S). For example, the University of South Florida campus is in zone 17 N. Within this zone the SCA building has the approximately UTM coordinates: 3104700 360830 E. The SCA building is about 3,104.7 km north of the equator. Example 1 Suppose a GPS gives the coordinate of a point in the MLK Plaza (MLK1) on the USF campus to be 3104941 N, 360912 E. How far north of the coordinate of the SCA building is MLK1? In [14] : mlk1_north = 3104941 #assign a variable to MLK1 northing sca_north = 3104700 #assign a variable to SCA northing distance_north = mki_north - sca_north #difference the value print("distance = ", distance_north, "m") #print the answer distance = 241 m Problem 1 - solve with a python script How far East of the coordinate of the SCA building is MLK1? Hint. Follow the same procedure as given in example #1 In [ ]: Problem 2 What is the coordinate of a point 100 m west of the MLK Plaza point (MLK2)? In [ ]: Problem 3 What is the UTM coordinate of a point located in zone 17, 100 m west of the central meridian and 130 m south of the equator? Hint, remember that the northing coordinate of the equator is 10,000,000 m, for points located in the southern hemisphere. Also remember that the easting coordinate of any central meridian (there are 60!) is 500,000 E. In (): Problem 4 A USF MS student, John Petriello, did a GPR survey on deposits from Puluagua volcano, Ecuador. The deposits, and John's survey line, crossed the equator. This created an offset in the northing coordinates along John's line at the equator. To solve this problem, John created a local grid using the UTM coordinates of the southern hemuisphere even for points located along the survey line in the northern hemisphere. That is, in John's local grid, a point located 100 m north of the equator would have the northing coordinate 10000100 N, which is not an allowable UTM coordinate but is a fine value for the local grid. Unfortunately, John's GPS report locations in UTM coordinates, not in his local grid coordinates. The coordinates of the beginning and end points along John's survey line, in real UTM coordinates, are: First Point: 9999564,N, 785342, E zone 17, S Second Point 265 N, 785358 E zone 17, N Convert to these coordinates to John's local grid. In ( ): Background Often geoscientists want to make measurements along a line at even intervals, or on a map grid at even intervals. Example measurements made at even intervals might be the dip of a geologic bed, the depth to the water table, or the variation in the Earth's gravity. A schema: Beware that the measured interval is one less than the number of counts, unless the first count is zero. If you have N equally spaced stakes in the ground, there are N - 1 intervals between the stakes. Example 2 Two points, MLK1 and MLK2, are 100 m apart. Suppose you want to place stakes between MLK1 and MLK2 on a 10 m interval. The first stake is at MLK1, the second stake is 10 m west of MLK1, the last stake is at MLK2. How many stakes do you need? meters) number stakes = interval ( Cheerftake = 100+1 = 11 stakes stake In [15] : listance_apart = 100 #the two points are 100 m apart take_interval = 10 #the stakes are spaced at 10 m interval num_stakes = (100/10) + 1 #we need one more than the fraction - note the use of parenth brint("number of stakes = " , num_stakes) number of stakes = 11.0 Problem 4 Suppose you only have 10 stakes, and want them spaced evenly with the first stake at MLK1 and the last stake at MLK2. What is the distance between the stakes? Hint: (10 1) spaces x x spuce meter: 100 meters In [ ]: Problem 5 Suppose you want to create a 100 x 100 m grid of stakes, on a 10 m interval. How many stakes do you need? In [ ]: Problem 6 Suppose you only want to use 49 stakes to create a 100 x 100 direction. What is the interval? Hint: m grid with an even interval between stakes in each total distance 49 stakes = interval In [ ]: Problem 7 A satellite maps topography along a 2400 km-long transect in a N--S direction across North America. The satellite data are processed to provide one elevation measurement every 30 m of horizontal distance along the transect. How many elevation measurements are in the transect? In [ ]: Problem 8 A digital elevation model (DEM) is a map grid of elevation measurements. Usually, one axis of the grid runs N--S and the other axis runs E--W. If the southwesternmost corner of the DEM is located at 3200104 N, 500000 E, the spacing between elevation measurements in the grid is 30 m in both directions, and there are a total of 200 measurements in each direction, what is the UTM coordinate of the NE corner of the DEM? In [ ]: Background Originally the meter was intended to be defined in terms of the distance from the equator to the pole. Specifically, it was thought this distance is 10,000 kilometers. It turns out this is not exactly right, because the Earth is not quite spherical, and because at the time the meter was defined the distance between pole and equator was not precisely known. Nevertheless, it's close. To answer these questions, assume that the distance from the equator to the north pole is 10,000 kilometers and that the Earth is a perfect sphere. Problem 9 How many meters is it from the south pole to the equator? Hint: This is a question about unit conversion from kilometers to meters. In [ ]: Problem 10 Calculate the circumference of the Earth in kilometers. In [ ]: Example 3 Calculate the radius of the Earth. Recall that the circumference of a circle is 2nr , wherer is the radius. In [16]: #in order to use the value of PI and a lot of other math #import this module import math circumferance = 40000 #kilometers, right? #solve for radius #note pi is math.pi (because it is a feature of the math module) # note () in denominator to solve this equation correctly. radius = circumferance/(2*math.pi) print ("radius = ", radius, "km") radius = 6366.197723675814 km Problem 11 Since there are 60 UTM zones, what is the maximum width of a zone at the equator (in meters)? In ( ): Problem 12 Since the central meridian of a UTM zone is 500000 E, what are the maximum and minimum UTM Easting coordinates you would expect to find in any zone at the equator? In [ ]: Problem 13 The depth to the outer core is about 2900 km. What is the circumference of the Earth's outer core? In [ ]: Background A sphere has constant radius and the Earth does not. The equatorial radius of the Earth is approximately 6378.137 km, the polar radius of the Earth is approximately 6356.752 km. Consequently, the figure of the Earth is more precisely approximated by an oblate ellipsoid of revolution. The planet is flattened along its axis of rotation, its equatorial bulge a result of rotation. The Earth is wider around its waistline (the equator) than around the poles. The amount of flattening of the ellipsoid can be expressed in terms of equatorial and polar radii: Reg-Rpo f = Req equatorial and polar radii: Req- Rpo Req where Req is the radius of the Earth at the equator and Rpo is the radius at the pole. The magnitude of flattening, f , is now very well determined from observing artificial satellite orbits around the Earth, and is fixed for the WGS84 ellipsoid as f = 1/298.257223563 . Newton first discussed the flattening of the Earth, and estimated a value of 1/230. The radius of the Earth at a given latitude is given by RE= Reg 1 - fsinfo) where: RE is the Earth's radius at latitude , Req is the radius of the Earth at the equator, approximately 6378137 m, and f is the flattening. Problem 14 Based on height above sealevel, Mt. Everest (8,848 m above sealevel, about 28 degrees N) is the highest place on Earth. Cotopaxi volcano (5,897 m above sealevel, about 1 degree N) is also a very high mountain. What if we measured height with respect to the center of the Earth? Which is taller: Cotopaxi or Everest? Hint: For distance from the center of the Earth of Mt Everest: = 6378.137(1 - (1/298.257) sin 28) + 8.848 = 6382.272 km In [18] : this bit of code solves the hint you have to write the rest of the code to solve this problem! import the math module mport math specify earth parameters quatorial_radius = 6378.137 #kilometers lattening = 1/298.257 info needed about Mt. Everest atitude_mt_everest = 28 #degrees eight_mt_everest = 8.848 #kilometers step 1 - convert latitude to radians python does caluclations in radians adians_mt_everest = 28 * math.pi/180 step 2 - find distance of the top of Mt Everest from center of earth listance_mt_everest = equatorial_radius*(1-flattening*math.sin(radians_mt_everest)**2) + rint ("distance of Mt Everest from earth center = ", distance_mt_everest, "km") now complete the code making the same calculation for Cotopaxi and compare the results distance of Mt Everest from earth center = 6382.271735848219 km Background Latitude and longitude can be expressed in decimal degrees (for example, MLK1:28.0626 N, 82.4153 W) or in degrees, minutes and seconds. To convert 28.0626 N to degrees and minutes, express the latitude with a whole number and a remainder. The remainder is multiplied by 60, because there are 60 minutes in 1 degree. 28.0626 N = 28 + 0.0626 x 60 minutes/degree = 28 3.756' To convert to degrees, minutes, and seconds the minutes must be treated as a whole number and remainder that is multiplied by 60, because there are 60 seconds in one minute. 28 3.756' N = 28 + 3 +0.756' x 60 seconds/minute = 283'45.36" N Problem 15 Convert the longitude 82.4153 W to degrees minutes seconds In [ ]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


