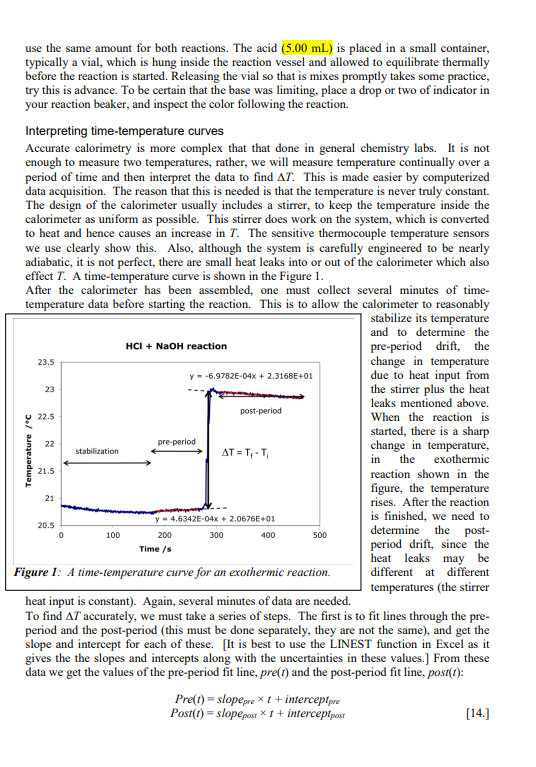
I NEED HELP IN SOLVING THE ENTHALPIES AND HEAT OF FORMATIONS FOR EQUATIONS 11-13. AS WELL AS THE CALCULATIONS OF SOLVING FOR Ccal PLEASE.

Objective You will determine the enthalpy of an weak acid- strong base neutralization reaction and from that data, determine the enthalpy of dissociation of a weak acid. You will do this in a solution calorimeter, measuring temperature changes upon reactions, and use the heat capacity of the system and your knowledge of thermochemistry to find H. Introduction The Principles of Calorimetry We want to determine experimentally the enthalpy change of a reaction. Therefore we will measure the heat of the reaction, since at constant pressure, qp=H. Likewise at constant volume, such as found in the bomb calorimeter, qv=U=H(PV). The state function H is a function of T, so to measure the enthalpy of a reaction from A to B at a temperature Tl, we need the reaction: A(T1)H1B(T1) So H1=H(T1). A practical problem arises immediately. When we perform calorimetry experimentally, we usually do it in a well-insulated, adiabatic calorimeter, and we measure a temperature change, therefore the products of the reaction are not usually at the same temperature as the reactants were initially. There is also the added complication that the calorimeter has a non-zero heat capacity. The reaction we actually measure is: A(T1)+Cal(T1)H2B(T2)+Cal(T2) Since the calorimeter is adiabatic, q=0. At constant pressure, this means qP=H2=0. This doesn't mean that the enthalpy of the reaction is zero! The enthalpy of the reaction at T1 is given by equation [1], not equation [2]. To get meaningful results, we need one more process: B(T2)+Cal(T2)H3B(T1)+Cal(T1) Since H is a state function, adding reactions [2] + [3] gives [1]. Therefore at constant pressure H(T1)=H2+H3=H3=q3 and at constant volume U(T1)=U2+U3=U3=q3 where q3 is the heat of reaction [3]. We can find the value of q3 from the heat capacity of the calorimeter and the reaction products. In condensed phase, CPCV=C, so q3=Ccal(T1T2) where Ccal is the heat capacity of the calorimeter (including any solvent and other chemical species present). Often we reverse the order of T1 and T2, since in [2], the reaction we actually perform, T2 is the final temperature. q3Ccal(T2T1)=CcalT Note that there is no need to actually perform reaction [3], we just need to know the value of Ccal, we get T1 and T2 from performing reaction [2]. Heat capacity of the calorimeter There are two techniques for determining the heat capacity of the calorimeter. The first technique is to perform a reaction in the calorimeter in which the heat of the reaction is wellknown (a standard reaction). A common reaction used in solution calorimetry is HCl+TRIS (a common buffer in biochemistry). We will use HCl (aq) +NaOH (aq) in this experiment. You need to determine the molar enthalpy for the reaction using available thermodynamic data, either from textbooks or handbooks. Measuring T for the reaction and knowing the number of moles reacted and allows the determination of Ccal by combining equations [4] and [7]: Tq=TnHm=Ccal In this method, it is important to keep all the factors that contribute to Ccal as constant as possible, particularly the mass of solvent (solution calorimeter). Details on solution calorimeter heat capacity: Note that the heat capacity Ccal discussed in the section above is the total heat capacity of the full solution calorimeter. In the solution calorimeter, this value of Ccal is then further analyzed to find the heat capacity of the empty calorimeter alone. The total heat capacity is the sum of the heat capacities of the empty calorimeter, the solvent and the solute: Ccal=Cemptycalorimeter+Csolvent+CsoluteCemptycallorimecer+Csolvent Normally Csolute is very small and is ignored. The heat capacity of the solvent is calculated from the specific heat capacity (S) of the solvent times its mass (m). Consequently, the heat capacity of the empty calorimeter is: Cemptycalcorimeter=CcalCsolvent=CcalmS Knowing CemptycalorimeterandS allows us to calculate Ccal when we make calorimeter runs with different values for the mass of the solution, m. This is explained in detail in the calorimeter operating instructions. Enthalpy for dissociation of a weak acid In this experiment you will determine the enthalpy of dissociation of a weak acid, in this case, acetic acid. HCH3COO(aq)H+(aq)+CH3COO(aq) A difficulty immediately arises because the reaction strongly favors the left side, and is very far from complete. Consequently, we must measure a different reaction which is complete: HCH3COO(aq)+OH(aq)H2O(l)+CH3COO(aq) We are already using the following reaction to calibrate the heat capacity of the calorimeter: H+(aq)+OH(aq)H2O(l) Using Hess" Law, you should be able to determine the enthalpy of the reaction in [11] using the enthalpies of reaction for [12] and [13]. Since you are using [13] for calibration of the heat capacity (see [8]), you cannot determine its enthalpy independently, so you must use the literature value for that reaction. The enthalpy of [12] should be determined experimentally, or else this becomes a dry lab. Experimental You will perform the reactions in either a Dewar flask or an insulated beaker. Temperature data will be recorded using thermocouples; these sensitive devices can readily measure millikelvin temperature changes. They are connected to a computer interface device which operates under a datalogger program: this program records time-temperature curves directly, typically at about 2 points per second in this context. The file from the datalogger can be conveniently exported to Excel, and it can record multiple thermocouples simultaneously, so several groups can share one computer. Reagents: acetic acid (2.5M), hydrochloric acid (2.5M), sodium hydroxide (0.2M), phenolphthalein or bromothymal blue indicator (solutions prepared by stockroom) This experiment works best if the temperature rises are approximately 12C: too large a temperature rise creates noticeable heat leaks in the reaction post-period, too small a rise give poor precision. The quantities of reagents are chosen to give temperature changes in this range. Since NaOH is used in both reactions, it makes the analysis far more convenient to choose this to be the limiting reagent, and to use the same quantity in both reactions. The easiest way to get the quantities the same for both reactions is to weight the solution into dry beakers. A mass of 50g works well, the precise quantity is not important, but you need to use the same amount for both reactions. The acid (5.00mL) is placed in a small container, typically a vial, which is hung inside the reaction vessel and allowed to equilibrate thermally before the reaction is started. Releasing the vial so that is mixes promptly takes some practice, try this is advance. To be certain that the base was limiting, place a drop or two of indicator in your reaction beaker, and inspect the color following the reaction. Interpreting time-temperature curves Accurate calorimetry is more complex that that done in general chemistry labs. It is not enough to measure two temperatures, rather, we will measure temperature continually over a period of time and then interpret the data to find T. This is made easier by computerized data acquisition. The reason that this is needed is that the temperature is never truly constant. The design of the calorimeter usually includes a stirrer, to keep the temperature inside the calorimeter as uniform as possible. This stirrer does work on the system, which is converted to heat and hence causes an increase in T. The sensitive thermocouple temperature sensors we use clearly show this. Also, although the system is carefully engineered to be nearly adiabatic, it is not perfect, there are small heat leaks into or out of the calorimeter which also effect T. A time-temperature curve is shown in the Figure 1. After the calorimeter has been assembled, one must collect several minutes of timetemperature data before starting the reaction. This is to allow the calorimeter to reasonably stabilize its temperature and to determine the pre-period drift, the change in temperature due to heat input from the stirrer plus the heat leaks mentioned above. When the reaction is started, there is a sharp change in temperature, in the exothermic reaction shown in the figure, the temperature rises. After the reaction is finished, we need to determine the postperiod drift, since the heat leaks may be different at different temperatures (the stirrer heat input is constant). Again, several minutes of data are needed. To find T accurately, we must take a series of steps. The first is to fit lines through the preperiod and the post-period (this must be done separately, they are not the same), and get the slope and intercept for each of these. [It is best to use the LINEST function in Excel as it gives the the slopes and intercepts along with the uncertainties in these values.] From these data we get the values of the pre-period fit line, pre (t) and the post-period fit line, post(t) : Pre(t)Post(t)=slopepret+interceptpre=slopepastt+interceptpost Next we find the time t during the reaction period which is approximately halfway through the sharp temperature rise, we will call this time tran. (More complex methods have been developed to determine this value, but since the temperature rise is very rapid in this experiment and the slopes are rather small numbers, this approximation is adequate.) Using this value plus the slope and intercept data in [11] we can determine the value of T : Ti=slopepretpxu+intercepttpreTf=slopeposttnxn+interceptpast The example shown is for an exothermic reaction, but the method is just the same for an endothermic reaction, it just gives a negative value of T. Data analysis The concentration listed on the NaOH is only approximate. While you may titrate it to determine this more precisely, that is in fact unnecessary (see below). As long as the acids used are in excess, their precise concentrations are unimportant. The molar enthalpy of the weak acid-strong base reaction listed in [12], applying equation [8] is given by: Hm,mal=nCcalTabiz The strong acid-strong base reaction is used to find the calorimeter heat capacity: TstrougnHm,stroug=Ccal If the number of moles of the limiting reagent, n, and the mass of the solution , m see [9] and [10], is the same in both reactions, we can combine the above two equations in a simple form: Hwr,mank=TstroagHm,trangTweak You will then need to apply Hess' Law to determine the enthalpy of the reaction in [11]. As mentioned above, equation [15] can be used to find the temperature change values for each intercept tpas and tnx You may ignore the uncertainty in trxn, but you must use the uncertainties of the slopes and intercepts to find the uncertainties in each of the T values (strong and weak). With this information, you can find the uncertainty in your enthalpy values. Objective You will determine the enthalpy of an weak acid- strong base neutralization reaction and from that data, determine the enthalpy of dissociation of a weak acid. You will do this in a solution calorimeter, measuring temperature changes upon reactions, and use the heat capacity of the system and your knowledge of thermochemistry to find H. Introduction The Principles of Calorimetry We want to determine experimentally the enthalpy change of a reaction. Therefore we will measure the heat of the reaction, since at constant pressure, qp=H. Likewise at constant volume, such as found in the bomb calorimeter, qv=U=H(PV). The state function H is a function of T, so to measure the enthalpy of a reaction from A to B at a temperature Tl, we need the reaction: A(T1)H1B(T1) So H1=H(T1). A practical problem arises immediately. When we perform calorimetry experimentally, we usually do it in a well-insulated, adiabatic calorimeter, and we measure a temperature change, therefore the products of the reaction are not usually at the same temperature as the reactants were initially. There is also the added complication that the calorimeter has a non-zero heat capacity. The reaction we actually measure is: A(T1)+Cal(T1)H2B(T2)+Cal(T2) Since the calorimeter is adiabatic, q=0. At constant pressure, this means qP=H2=0. This doesn't mean that the enthalpy of the reaction is zero! The enthalpy of the reaction at T1 is given by equation [1], not equation [2]. To get meaningful results, we need one more process: B(T2)+Cal(T2)H3B(T1)+Cal(T1) Since H is a state function, adding reactions [2] + [3] gives [1]. Therefore at constant pressure H(T1)=H2+H3=H3=q3 and at constant volume U(T1)=U2+U3=U3=q3 where q3 is the heat of reaction [3]. We can find the value of q3 from the heat capacity of the calorimeter and the reaction products. In condensed phase, CPCV=C, so q3=Ccal(T1T2) where Ccal is the heat capacity of the calorimeter (including any solvent and other chemical species present). Often we reverse the order of T1 and T2, since in [2], the reaction we actually perform, T2 is the final temperature. q3Ccal(T2T1)=CcalT Note that there is no need to actually perform reaction [3], we just need to know the value of Ccal, we get T1 and T2 from performing reaction [2]. Heat capacity of the calorimeter There are two techniques for determining the heat capacity of the calorimeter. The first technique is to perform a reaction in the calorimeter in which the heat of the reaction is wellknown (a standard reaction). A common reaction used in solution calorimetry is HCl+TRIS (a common buffer in biochemistry). We will use HCl (aq) +NaOH (aq) in this experiment. You need to determine the molar enthalpy for the reaction using available thermodynamic data, either from textbooks or handbooks. Measuring T for the reaction and knowing the number of moles reacted and allows the determination of Ccal by combining equations [4] and [7]: Tq=TnHm=Ccal In this method, it is important to keep all the factors that contribute to Ccal as constant as possible, particularly the mass of solvent (solution calorimeter). Details on solution calorimeter heat capacity: Note that the heat capacity Ccal discussed in the section above is the total heat capacity of the full solution calorimeter. In the solution calorimeter, this value of Ccal is then further analyzed to find the heat capacity of the empty calorimeter alone. The total heat capacity is the sum of the heat capacities of the empty calorimeter, the solvent and the solute: Ccal=Cemptycalorimeter+Csolvent+CsoluteCemptycallorimecer+Csolvent Normally Csolute is very small and is ignored. The heat capacity of the solvent is calculated from the specific heat capacity (S) of the solvent times its mass (m). Consequently, the heat capacity of the empty calorimeter is: Cemptycalcorimeter=CcalCsolvent=CcalmS Knowing CemptycalorimeterandS allows us to calculate Ccal when we make calorimeter runs with different values for the mass of the solution, m. This is explained in detail in the calorimeter operating instructions. Enthalpy for dissociation of a weak acid In this experiment you will determine the enthalpy of dissociation of a weak acid, in this case, acetic acid. HCH3COO(aq)H+(aq)+CH3COO(aq) A difficulty immediately arises because the reaction strongly favors the left side, and is very far from complete. Consequently, we must measure a different reaction which is complete: HCH3COO(aq)+OH(aq)H2O(l)+CH3COO(aq) We are already using the following reaction to calibrate the heat capacity of the calorimeter: H+(aq)+OH(aq)H2O(l) Using Hess" Law, you should be able to determine the enthalpy of the reaction in [11] using the enthalpies of reaction for [12] and [13]. Since you are using [13] for calibration of the heat capacity (see [8]), you cannot determine its enthalpy independently, so you must use the literature value for that reaction. The enthalpy of [12] should be determined experimentally, or else this becomes a dry lab. Experimental You will perform the reactions in either a Dewar flask or an insulated beaker. Temperature data will be recorded using thermocouples; these sensitive devices can readily measure millikelvin temperature changes. They are connected to a computer interface device which operates under a datalogger program: this program records time-temperature curves directly, typically at about 2 points per second in this context. The file from the datalogger can be conveniently exported to Excel, and it can record multiple thermocouples simultaneously, so several groups can share one computer. Reagents: acetic acid (2.5M), hydrochloric acid (2.5M), sodium hydroxide (0.2M), phenolphthalein or bromothymal blue indicator (solutions prepared by stockroom) This experiment works best if the temperature rises are approximately 12C: too large a temperature rise creates noticeable heat leaks in the reaction post-period, too small a rise give poor precision. The quantities of reagents are chosen to give temperature changes in this range. Since NaOH is used in both reactions, it makes the analysis far more convenient to choose this to be the limiting reagent, and to use the same quantity in both reactions. The easiest way to get the quantities the same for both reactions is to weight the solution into dry beakers. A mass of 50g works well, the precise quantity is not important, but you need to use the same amount for both reactions. The acid (5.00mL) is placed in a small container, typically a vial, which is hung inside the reaction vessel and allowed to equilibrate thermally before the reaction is started. Releasing the vial so that is mixes promptly takes some practice, try this is advance. To be certain that the base was limiting, place a drop or two of indicator in your reaction beaker, and inspect the color following the reaction. Interpreting time-temperature curves Accurate calorimetry is more complex that that done in general chemistry labs. It is not enough to measure two temperatures, rather, we will measure temperature continually over a period of time and then interpret the data to find T. This is made easier by computerized data acquisition. The reason that this is needed is that the temperature is never truly constant. The design of the calorimeter usually includes a stirrer, to keep the temperature inside the calorimeter as uniform as possible. This stirrer does work on the system, which is converted to heat and hence causes an increase in T. The sensitive thermocouple temperature sensors we use clearly show this. Also, although the system is carefully engineered to be nearly adiabatic, it is not perfect, there are small heat leaks into or out of the calorimeter which also effect T. A time-temperature curve is shown in the Figure 1. After the calorimeter has been assembled, one must collect several minutes of timetemperature data before starting the reaction. This is to allow the calorimeter to reasonably stabilize its temperature and to determine the pre-period drift, the change in temperature due to heat input from the stirrer plus the heat leaks mentioned above. When the reaction is started, there is a sharp change in temperature, in the exothermic reaction shown in the figure, the temperature rises. After the reaction is finished, we need to determine the postperiod drift, since the heat leaks may be different at different temperatures (the stirrer heat input is constant). Again, several minutes of data are needed. To find T accurately, we must take a series of steps. The first is to fit lines through the preperiod and the post-period (this must be done separately, they are not the same), and get the slope and intercept for each of these. [It is best to use the LINEST function in Excel as it gives the the slopes and intercepts along with the uncertainties in these values.] From these data we get the values of the pre-period fit line, pre (t) and the post-period fit line, post(t) : Pre(t)Post(t)=slopepret+interceptpre=slopepastt+interceptpost Next we find the time t during the reaction period which is approximately halfway through the sharp temperature rise, we will call this time tran. (More complex methods have been developed to determine this value, but since the temperature rise is very rapid in this experiment and the slopes are rather small numbers, this approximation is adequate.) Using this value plus the slope and intercept data in [11] we can determine the value of T : Ti=slopepretpxu+intercepttpreTf=slopeposttnxn+interceptpast The example shown is for an exothermic reaction, but the method is just the same for an endothermic reaction, it just gives a negative value of T. Data analysis The concentration listed on the NaOH is only approximate. While you may titrate it to determine this more precisely, that is in fact unnecessary (see below). As long as the acids used are in excess, their precise concentrations are unimportant. The molar enthalpy of the weak acid-strong base reaction listed in [12], applying equation [8] is given by: Hm,mal=nCcalTabiz The strong acid-strong base reaction is used to find the calorimeter heat capacity: TstrougnHm,stroug=Ccal If the number of moles of the limiting reagent, n, and the mass of the solution , m see [9] and [10], is the same in both reactions, we can combine the above two equations in a simple form: Hwr,mank=TstroagHm,trangTweak You will then need to apply Hess' Law to determine the enthalpy of the reaction in [11]. As mentioned above, equation [15] can be used to find the temperature change values for each intercept tpas and tnx You may ignore the uncertainty in trxn, but you must use the uncertainties of the slopes and intercepts to find the uncertainties in each of the T values (strong and weak). With this information, you can find the uncertainty in your enthalpy values