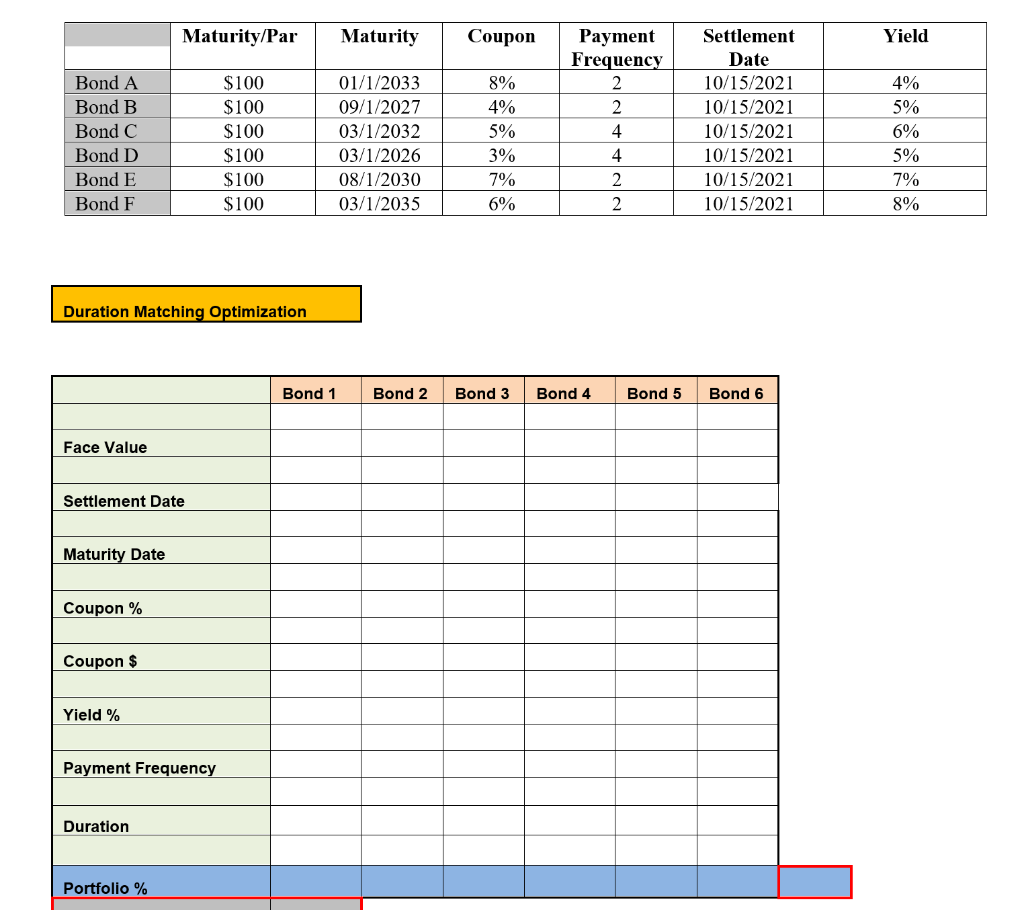
I need help using solver in excel

8.7.1

Optimization: Bond Durations Matching Bonds are generally considered less risky than stocks. Students should be familiar with the inverse relationship of interest rates and bond prices. The higher the credit quality of the bond issuer the stronger this relationship such that if a bond is of the highest credit quality, i.e., government treasuries its price change is almost entirely dependent upon interest rate changes. If interest rates go up, the price of the bond will go down. Conversely, if interest rates go down the bond's price will rise. However, there can be an offset to the investor as most bonds pay interest in an annual (or semi-annual) coupon, and the interest can be reinvested at current interest rates. As an example, if interest rates go up, the price of the bond will go down but the coupon interest paid can be reinvested at the higher rates of interest. These two effects cancel each other out at the end of the duration of a bond. The duration of a bond is the average time in which a bond is repaid. For example, if a bond has a maturity of 3 years with a face value of $100 and an annual coupon payment of $10 and yield to maturity of 10%, the duration is 2.735 years. Thus, one way of protecting against fluctuation of interest rates is to have a portfolio whose duration is equal to one's own investment time horizon. A portfolio of bonds has a duration that is weighted average of the duration of the individual bonds. In the model we assume we know the duration of the bonds available and want to maximize the yield of the portfolio while keeping the duration equal to a given investment time horizon. This technique is known as bond portfolio immunization. Bond Immunization Model An investor wants to put together a portfolio, consisting of portions of 6 different bonds. What is the best combination of bonds to get the optimum yield with a given investment time horizon? The period from settlement to maturity varies for each bond Problem An investor wants to put together a portfolio consisting of up to 6 different bonds. To minimize risk of loss of principal value due to interest rate fluctuations and to assure enough cash flow at a certain point in the future, she wants to make sure the average duration of the bonds equals her investment time horizon. How should the investor choose her portfolio to optimize the combined yield of the bonds, while making sure the duration of the portfolio equals the investment time horizon? The bonds in question have various maturity dates as well and coupon payment frequencies. The annual payments, the yield and the face value of the bonds are all known. Solution The objective is to maximize the portfolio yield under an investment time horizon of 6 years. a. Target Cell: Maximize the target cell of the portfolio yield b. Changing Cells: These are the individual percentage holdings of each individual Bond. c. Constraints: Portfolio Duration must equal the investment time horizon. Each bond holding cannot be less than 0 Portfolio Yield must be at least 6% Sum of the percentage holding of bonds must be equal to 100% Maturity/Par Maturity Coupon Yield Bond A Bond B Bond C Bond D Bond E Bond F $100 $100 $100 $100 $100 $100 01/1/2033 09/1/2027 03/1/2032 03/1/2026 08/1/2030 03/1/2035 8% 4% 5% 3% 7% 6% Payment Frequency 2 2 4 4 2 2 Settlement Date 10/15/2021 10/15/2021 10/15/2021 10/15/2021 10/15/2021 10/15/2021 4% 5% 6% 5% 7% 8% Duration Matching Optimization Bond 1 Bond 2 Bond 3 Bond 4 Bond 5 Bond 6 Face Value Settlement Date Maturity Date Coupon % Coupon $ Yield % Payment Frequency Duration Portfolio % Investment Time Horizon Portfolio Duration Portfolio Yield Optimization: Bond Durations Matching Bonds are generally considered less risky than stocks. Students should be familiar with the inverse relationship of interest rates and bond prices. The higher the credit quality of the bond issuer the stronger this relationship such that if a bond is of the highest credit quality, i.e., government treasuries its price change is almost entirely dependent upon interest rate changes. If interest rates go up, the price of the bond will go down. Conversely, if interest rates go down the bond's price will rise. However, there can be an offset to the investor as most bonds pay interest in an annual (or semi-annual) coupon, and the interest can be reinvested at current interest rates. As an example, if interest rates go up, the price of the bond will go down but the coupon interest paid can be reinvested at the higher rates of interest. These two effects cancel each other out at the end of the duration of a bond. The duration of a bond is the average time in which a bond is repaid. For example, if a bond has a maturity of 3 years with a face value of $100 and an annual coupon payment of $10 and yield to maturity of 10%, the duration is 2.735 years. Thus, one way of protecting against fluctuation of interest rates is to have a portfolio whose duration is equal to one's own investment time horizon. A portfolio of bonds has a duration that is weighted average of the duration of the individual bonds. In the model we assume we know the duration of the bonds available and want to maximize the yield of the portfolio while keeping the duration equal to a given investment time horizon. This technique is known as bond portfolio immunization. Bond Immunization Model An investor wants to put together a portfolio, consisting of portions of 6 different bonds. What is the best combination of bonds to get the optimum yield with a given investment time horizon? The period from settlement to maturity varies for each bond Problem An investor wants to put together a portfolio consisting of up to 6 different bonds. To minimize risk of loss of principal value due to interest rate fluctuations and to assure enough cash flow at a certain point in the future, she wants to make sure the average duration of the bonds equals her investment time horizon. How should the investor choose her portfolio to optimize the combined yield of the bonds, while making sure the duration of the portfolio equals the investment time horizon? The bonds in question have various maturity dates as well and coupon payment frequencies. The annual payments, the yield and the face value of the bonds are all known. Solution The objective is to maximize the portfolio yield under an investment time horizon of 6 years. a. Target Cell: Maximize the target cell of the portfolio yield b. Changing Cells: These are the individual percentage holdings of each individual Bond. c. Constraints: Portfolio Duration must equal the investment time horizon. Each bond holding cannot be less than 0 Portfolio Yield must be at least 6% Sum of the percentage holding of bonds must be equal to 100% Maturity/Par Maturity Coupon Yield Bond A Bond B Bond C Bond D Bond E Bond F $100 $100 $100 $100 $100 $100 01/1/2033 09/1/2027 03/1/2032 03/1/2026 08/1/2030 03/1/2035 8% 4% 5% 3% 7% 6% Payment Frequency 2 2 4 4 2 2 Settlement Date 10/15/2021 10/15/2021 10/15/2021 10/15/2021 10/15/2021 10/15/2021 4% 5% 6% 5% 7% 8% Duration Matching Optimization Bond 1 Bond 2 Bond 3 Bond 4 Bond 5 Bond 6 Face Value Settlement Date Maturity Date Coupon % Coupon $ Yield % Payment Frequency Duration Portfolio % Investment Time Horizon Portfolio Duration Portfolio Yield