I need help writing this code in python for this assingment.

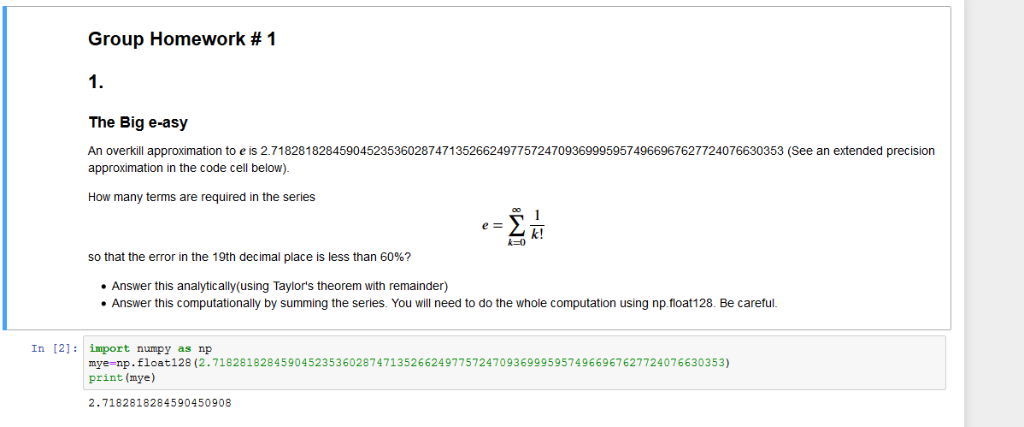
Group Homework # 1 1. The Big e-asy An overkill approximation to e is 2.718281828459045235360287471352662497757247093699959574966967627724076630353 (See an extended precision approximation in the code cell below). How many terms are required in the series k! so that the error in the 19th decimal place is less than 60%? Answer this analytically(using Taylor's theorem with remainder) Answer this computationally by summing the series. You will need to do the whole computation using np float128. Be careful. In [2]: import numpy as np mye-np.float128 (2.718281828459045235360287471352662497757247093699959574966967627724076630353) print (mye) 2.7182818284590450908 2. All Wrong Consider x)tanx- What is the smallest value of p such that f(10P) has no significant digits? (Hint-conider the limit as x0). . come up with a more accurate representation for small x(Hint use enough terms of the Taylor series of tan x near x = 0, and test it for very small x 3. Mean Business In class, we showed that the geometric mean of n positive numbers was prone to overflow or underflow if the power was taken at the end. Come up with a compromise solution to the computation that avoids overflows and underflows but is faster than Bonus +3 points to the group with the fastest algorithm Group Homework # 1 1. The Big e-asy An overkill approximation to e is 2.718281828459045235360287471352662497757247093699959574966967627724076630353 (See an extended precision approximation in the code cell below). How many terms are required in the series k! so that the error in the 19th decimal place is less than 60%? Answer this analytically(using Taylor's theorem with remainder) Answer this computationally by summing the series. You will need to do the whole computation using np float128. Be careful. In [2]: import numpy as np mye-np.float128 (2.718281828459045235360287471352662497757247093699959574966967627724076630353) print (mye) 2.7182818284590450908 2. All Wrong Consider x)tanx- What is the smallest value of p such that f(10P) has no significant digits? (Hint-conider the limit as x0). . come up with a more accurate representation for small x(Hint use enough terms of the Taylor series of tan x near x = 0, and test it for very small x 3. Mean Business In class, we showed that the geometric mean of n positive numbers was prone to overflow or underflow if the power was taken at the end. Come up with a compromise solution to the computation that avoids overflows and underflows but is faster than Bonus +3 points to the group with the fastest algorithm