i need the excel file for part B!

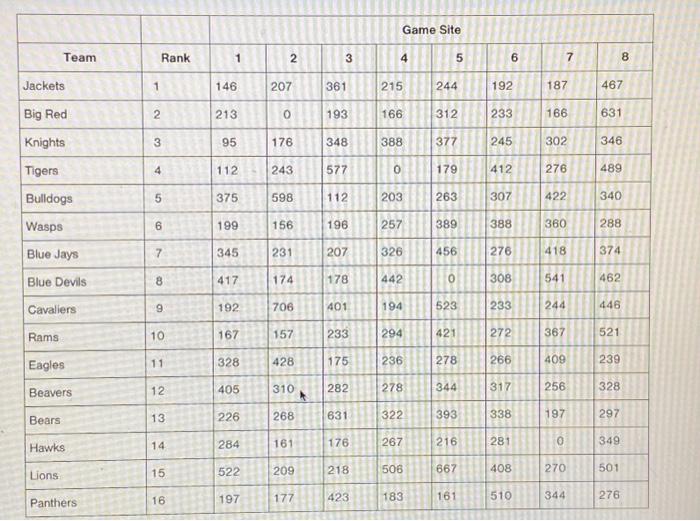
The National Collegiate Lacrosse Association is planning its annual national championship toumament. It selects 16 teams from conference champions and the highest ranked at-large teams to play in the singleelimination tournament. The teams are ranked from 1 (best) to 16 (worst), and in the first round of the tournament, the association wants to pair the teams so that high-ranked teams play low-ranked teams (i.e., seed them so that 1 plays 16. 2 plays 15, etc.). The eight first-round game sites are predetermined and have been selected based on stadium size and conditions, as well as historical local fan interest in lacrosse. Because of limited school budgets for lacrosse and a desire to boost game attendance, the association wants to assign teams to game sites so that all schools will have to travel the least amount possible. The following table shows the 16 teams in order of their ranking and the distance (in miles) for each of the teams to each of the eight game sites. a. Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines. b. Suppose the association wants to consider allowing some flexibility in pairing the teams according to their rankings (i. e.. seedings)-for example 1 might play 14 or 2 mighthalay 12 -in order to see to what extent averall team travel might be reduced. Retormulate and nolve the model to see what effect this might hive. The National Collegiate Lacrosse Association is planning its annual national championship toumament. It selects 16 teams from conference champions and the highest ranked at-large teams to play in the singleelimination tournament. The teams are ranked from 1 (best) to 16 (worst), and in the first round of the tournament, the association wants to pair the teams so that high-ranked teams play low-ranked teams (i.e., seed them so that 1 plays 16. 2 plays 15, etc.). The eight first-round game sites are predetermined and have been selected based on stadium size and conditions, as well as historical local fan interest in lacrosse. Because of limited school budgets for lacrosse and a desire to boost game attendance, the association wants to assign teams to game sites so that all schools will have to travel the least amount possible. The following table shows the 16 teams in order of their ranking and the distance (in miles) for each of the teams to each of the eight game sites. a. Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines. b. Suppose the association wants to consider allowing some flexibility in pairing the teams according to their rankings (i. e.. seedings)-for example 1 might play 14 or 2 mighthalay 12 -in order to see to what extent averall team travel might be reduced. Retormulate and nolve the model to see what effect this might hive