I need to answer the questions below, however I am having trouble with the math. Question a in particular, I use the equation out of the book N_P = [D_A - D_L ] x A / 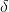x D x B, and cannot seem to come to the correct answer, which is 824. Any help with explaining the math would be greatly appreciated.

An FI has a $100 million portfolio of six-year Eurodollar bonds that have an 8 percent coupon. The bonds are trading at par and have a duration of five years. The FI wishes to hedge the portfolio with T-bond options that have a delta of -.0625. The underlying long-term Treasury bonds for the option have a duration of 10.1 years and trade at a market value of $96,157 per $100,000 of par value. Each put option has a premium of $3.25 per $100 of face value.

1. How many bond put options are necessary to hedge the bond portfolio?
2. If interest rates increase 100 basis points, what is the expected gain or loss on the put option hedge?
3. What is the expected change in market value on the bond portfolio?
4. What is the total cost of placing the hedge?
5. Diagram the payoff possibilities.
6. How far must interest rates move before the payoff on the hedge will exactly offset the cost of placing the hedge?
7. How far must interest rates move before the gain on the bond portfolio will exactly offset the cost of placing the hedge?
8. Summarize the gain, loss and cost conditions of the hedge on the bond portfolio in terms of changes in interest rates.