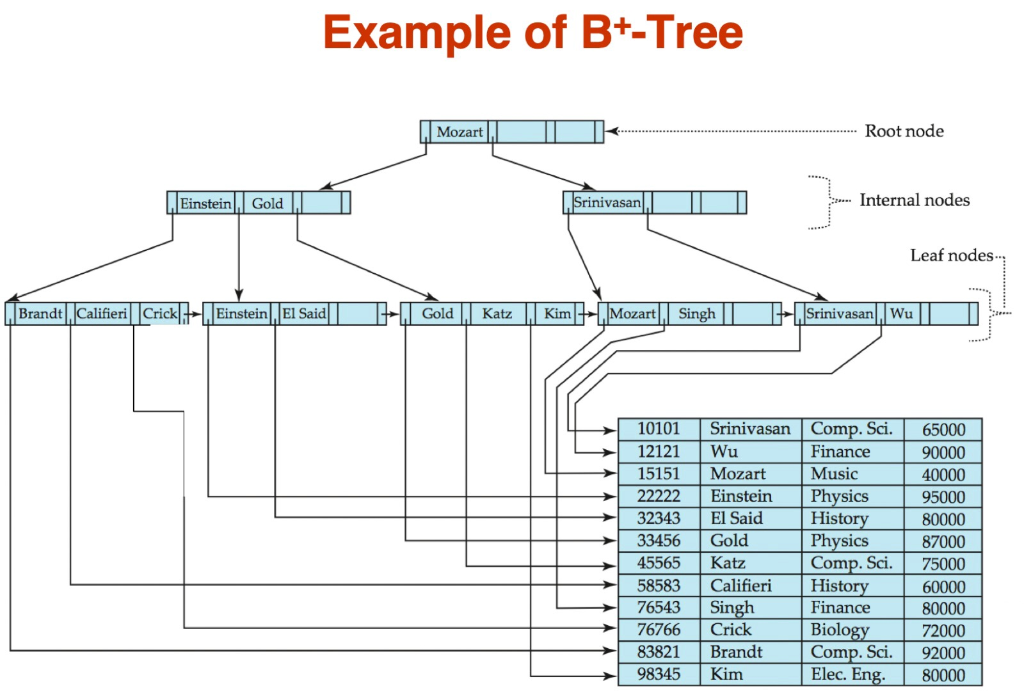
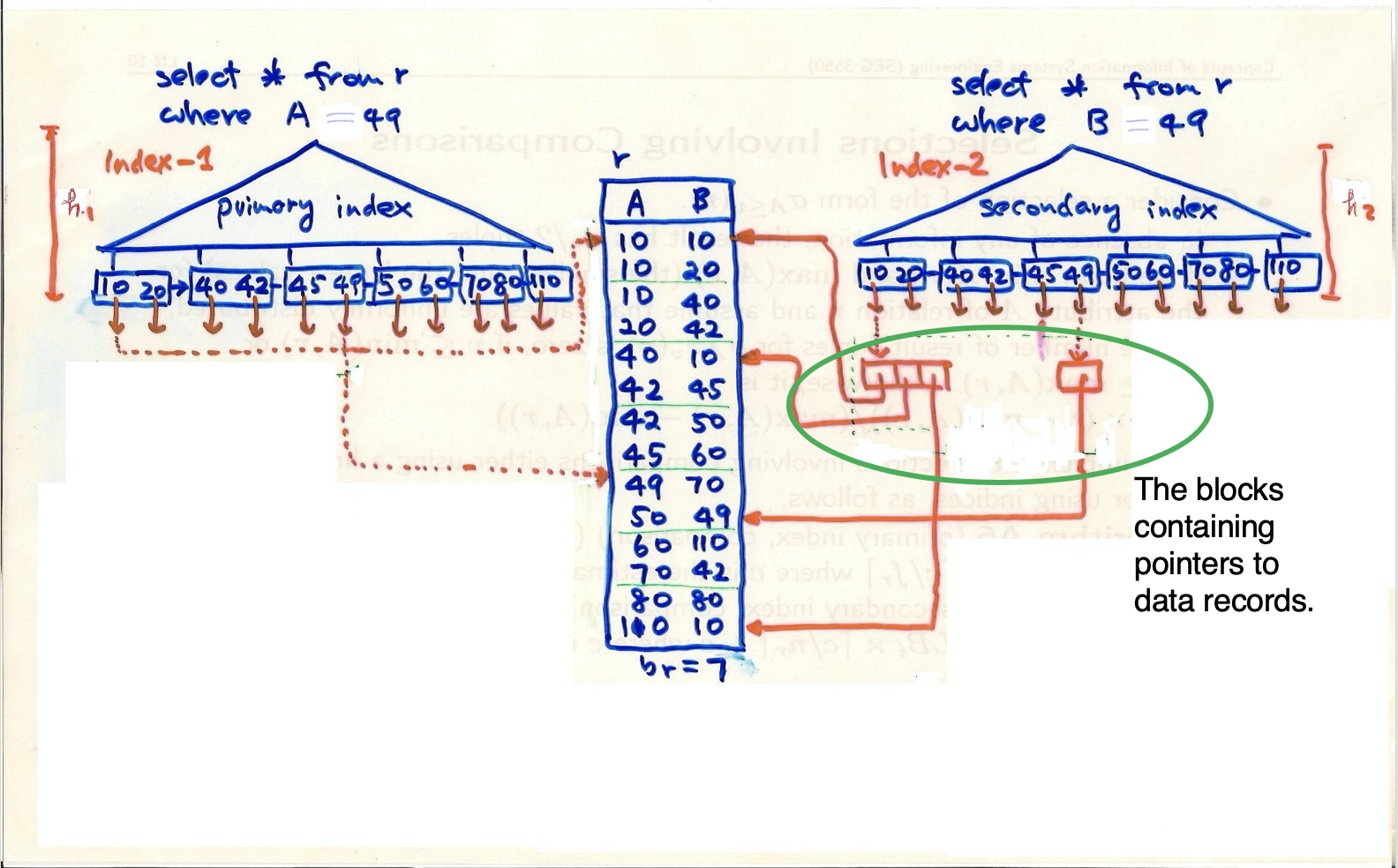
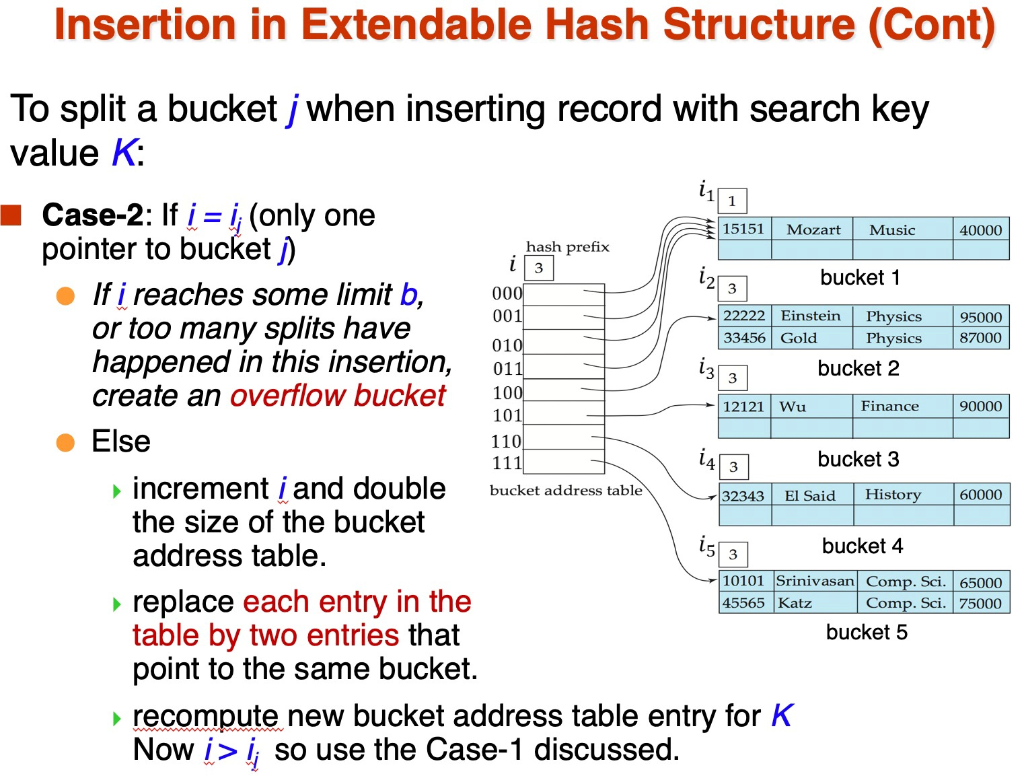
I Question 2: We discussed the merge-join algorithm for an equi-join r Nr. A=s.B s, when both relations are sorted in ch12.pptx. The pseudo code is shown in the slide 12.32 in ch12.pptx and discussed in Section 12.5.4 in the textbook. (1) Suppose that relation r is sorted on the attribute A but relation s is not sorted on the attribute B. Here, we assume that there is B+-tree, as a secondary index, built for the join attribute B in s. Recall that there are pointer and search key pairs, (pi, ki), in a leaf node in the secondary B+-tree. For a secondary B+-tree, such a pointer pi points to a list of pointers, Di = {d, d2,...}, where each dj = (bl, sk) points to a data record (or a tuple) that has the search key ki located at the slot sk in the block b in the data file using the slotted page structure (refer to the slide 10.14 in ch11.ppt for the slotted page structure and refer to the slide 12.10 in ch12.pptx for Di). Give a pseudo code to do this hybrid merge join" using the secondary B+-tree built on the attribute s.B. A naive approach is to do something using the similar idea presented in indexed nested-loop. Note that it does not make use of sorting for both the sorted attribute A and the secondary B+-tree built on B. You need to give an algorithm that utilizes the sorting on both sides (e.g., the sorted attribute A and the secondary B+-tree built on the attribute B), and minimizes the block transfers. Hint: for minimiz- ing the block transfer, you need to know the drawback of secondary B+-tree (refer to the slide 12.9 when we discuss the selection using indices). (2) Suppose that relation r is not sorted on the attribute A and the relation s is not sorted on the attribute B. However, there is a secondary B+-tree built for relation r on the attribute A and there is a secondary B+-tree built for relation s on the attribute B. Show a pseudo code to do this hybrid merge join making use of both secondary B+-trees to minimize the block transfer. Merge-Join (2) al a2 al a3 . 16 G dN m B S pr := address of first tuple of r; ps := address of first tuple of s; while (ps + null and pr + null) do begin ts := tuple to which ps points; Ss := {ts }; set ps to point to next tuple of s; done := false; while (not done and ps + null) do begin ts' := tuple to which ps points; if (ts' Join Attrs] = ts JoinAttrs]) then begin Ss := SU {ts'}; set ps to point to next tuple of s; end else done := true; end tr := tuple to which pr points; while (pr + null and tr[JoinAttrs] t to result; end set pr to point to next tuple of r; tr := tuple to which pr points; end end. Figure 12.7 Merge join. Example of B+-Tree | Mozart|| Mozart. | Root node Einstein, Gold, Srinivasan | | | - Internal nodes Leaf nodes poral calice (Erkel -Landes|| - | | Ca | Kata | Kim - Java | Songs || H-Lisemivast 10101 Srinivasan 12121 Wu 15151 Mozart 22222 Einstein 32343 El Said 33456 Gold 45565 Katz 58583 Califieri 76543 Singh 76766 Crick 83821 Brandt 98345 | Kim Comp. Sci. Finance Music Physics History Physics Comp. Sci. History Finance Biology Comp. Sci. Elec. Eng. 65000 90000 40000 95000 80000 87000 75000 60000 80000 72000 92000 80000 select * from where A = 49 Index=1 puinery index select * from r where B =49 Index-2 Secondary index hi gozpergo pesan foto 7882- 04 10 SO 600 The blocks containing pointers to data records. 80 1OO 10 br=7 Selections Using Indices A4 (secondary index, equality on nonkey). Retrieve a single record if the search key is a candidate key Cost = (h;+ 1) * (t1 + ts) Here, "on nonkev means the search key is not a candidate key. Note: a relation can have only one primary key, but may have several candidate keys. A primary key is a candidate key. Retrieve multiple records if the search-key is not a candidate key each of n matching records may be on a different block Cost = (hi + n) * (IT + ts) Can be very expensive! The number of accesses to the blocks that contain pointers to data records in the data file are ignored. Refer to the secondary index in ch 11. 15151 Mozart Music 40000 hash prefix 0001 001 010 22222 Einstein 33456 Gold Physics Physics 95000 87000 Insertion in Extendable Hash Structure (Cont) To split a bucket j when inserting record with search key value K: Case-2: If i = 1 (only one pointer to bucket ) If i reaches some limit b, 123) bucket 1 or too many splits have happened in this insertion, 011 133) bucket 2 create an overflow bucket Else 143) bucket 3 increment i and double 32343 El Said History the size of the bucket address table. 15 3 bucket 4 replace each entry in the table by two entries that point to the same bucket. recompute new bucket address table entry for K Now i > so use the Case-1 discussed. 12121 Wu Finance 90000 100 101 1101 111 bucket address table 60000 10101 Srinivasan Comp. Sci. 65000 45565 Katz Comp. Sci. 75000 bucket 5 I Question 2: We discussed the merge-join algorithm for an equi-join r Nr. A=s.B s, when both relations are sorted in ch12.pptx. The pseudo code is shown in the slide 12.32 in ch12.pptx and discussed in Section 12.5.4 in the textbook. (1) Suppose that relation r is sorted on the attribute A but relation s is not sorted on the attribute B. Here, we assume that there is B+-tree, as a secondary index, built for the join attribute B in s. Recall that there are pointer and search key pairs, (pi, ki), in a leaf node in the secondary B+-tree. For a secondary B+-tree, such a pointer pi points to a list of pointers, Di = {d, d2,...}, where each dj = (bl, sk) points to a data record (or a tuple) that has the search key ki located at the slot sk in the block b in the data file using the slotted page structure (refer to the slide 10.14 in ch11.ppt for the slotted page structure and refer to the slide 12.10 in ch12.pptx for Di). Give a pseudo code to do this hybrid merge join" using the secondary B+-tree built on the attribute s.B. A naive approach is to do something using the similar idea presented in indexed nested-loop. Note that it does not make use of sorting for both the sorted attribute A and the secondary B+-tree built on B. You need to give an algorithm that utilizes the sorting on both sides (e.g., the sorted attribute A and the secondary B+-tree built on the attribute B), and minimizes the block transfers. Hint: for minimiz- ing the block transfer, you need to know the drawback of secondary B+-tree (refer to the slide 12.9 when we discuss the selection using indices). (2) Suppose that relation r is not sorted on the attribute A and the relation s is not sorted on the attribute B. However, there is a secondary B+-tree built for relation r on the attribute A and there is a secondary B+-tree built for relation s on the attribute B. Show a pseudo code to do this hybrid merge join making use of both secondary B+-trees to minimize the block transfer. Merge-Join (2) al a2 al a3 . 16 G dN m B S pr := address of first tuple of r; ps := address of first tuple of s; while (ps + null and pr + null) do begin ts := tuple to which ps points; Ss := {ts }; set ps to point to next tuple of s; done := false; while (not done and ps + null) do begin ts' := tuple to which ps points; if (ts' Join Attrs] = ts JoinAttrs]) then begin Ss := SU {ts'}; set ps to point to next tuple of s; end else done := true; end tr := tuple to which pr points; while (pr + null and tr[JoinAttrs] t to result; end set pr to point to next tuple of r; tr := tuple to which pr points; end end. Figure 12.7 Merge join. Example of B+-Tree | Mozart|| Mozart. | Root node Einstein, Gold, Srinivasan | | | - Internal nodes Leaf nodes poral calice (Erkel -Landes|| - | | Ca | Kata | Kim - Java | Songs || H-Lisemivast 10101 Srinivasan 12121 Wu 15151 Mozart 22222 Einstein 32343 El Said 33456 Gold 45565 Katz 58583 Califieri 76543 Singh 76766 Crick 83821 Brandt 98345 | Kim Comp. Sci. Finance Music Physics History Physics Comp. Sci. History Finance Biology Comp. Sci. Elec. Eng. 65000 90000 40000 95000 80000 87000 75000 60000 80000 72000 92000 80000 select * from where A = 49 Index=1 puinery index select * from r where B =49 Index-2 Secondary index hi gozpergo pesan foto 7882- 04 10 SO 600 The blocks containing pointers to data records. 80 1OO 10 br=7 Selections Using Indices A4 (secondary index, equality on nonkey). Retrieve a single record if the search key is a candidate key Cost = (h;+ 1) * (t1 + ts) Here, "on nonkev means the search key is not a candidate key. Note: a relation can have only one primary key, but may have several candidate keys. A primary key is a candidate key. Retrieve multiple records if the search-key is not a candidate key each of n matching records may be on a different block Cost = (hi + n) * (IT + ts) Can be very expensive! The number of accesses to the blocks that contain pointers to data records in the data file are ignored. Refer to the secondary index in ch 11. 15151 Mozart Music 40000 hash prefix 0001 001 010 22222 Einstein 33456 Gold Physics Physics 95000 87000 Insertion in Extendable Hash Structure (Cont) To split a bucket j when inserting record with search key value K: Case-2: If i = 1 (only one pointer to bucket ) If i reaches some limit b, 123) bucket 1 or too many splits have happened in this insertion, 011 133) bucket 2 create an overflow bucket Else 143) bucket 3 increment i and double 32343 El Said History the size of the bucket address table. 15 3 bucket 4 replace each entry in the table by two entries that point to the same bucket. recompute new bucket address table entry for K Now i > so use the Case-1 discussed. 12121 Wu Finance 90000 100 101 1101 111 bucket address table 60000 10101 Srinivasan Comp. Sci. 65000 45565 Katz Comp. Sci. 75000 bucket 5