I want a full explanation step by step for this problem

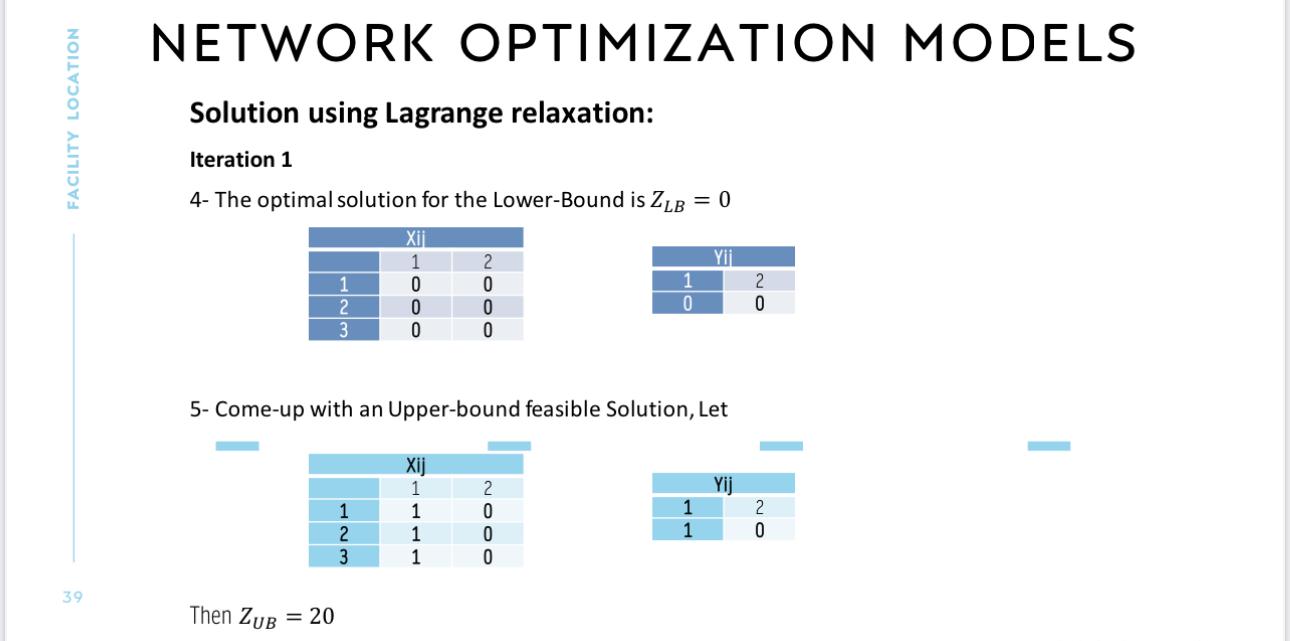
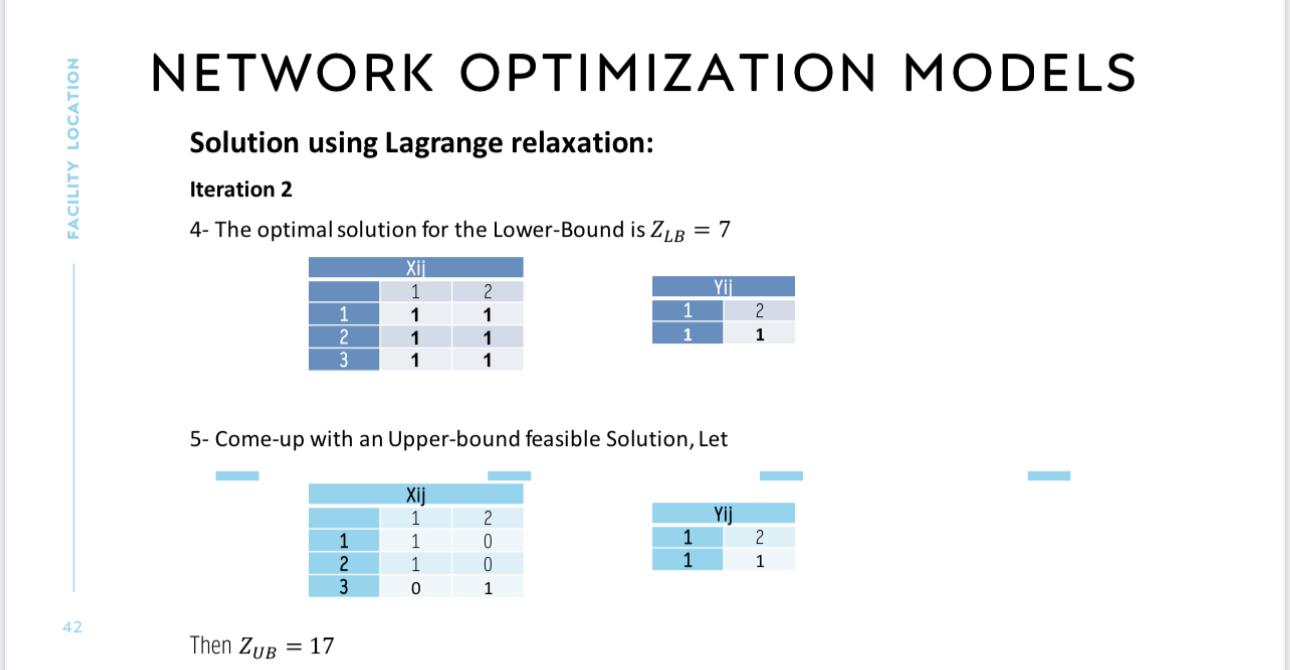
2-Fixed Charge Facility Location Problem Minj=1mfjYj+j=1mi=1ncijXij s.t 5. Network Optimization j=1mXij=1iIXijYjiI,jJXij,Yj{0,1} Example Let Models Set Covering Problem Fixed Charge Facility Location Problem Let fj=[23] and cij=549783 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: MaxMinj=1mfjYj+j=1mi=1ncijXij+i=1ni(1j=1mXij)s.tXijYjiI,jJXij,Yj{0,1} NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Solving Our example Min1+2+3+f1Y1+f2Y2+(c111)X11+(c212)X21+(c313)X31+(c121)X12+(c222)X22+(c323)X32s.tX11,X21,X31Y1X12,X22,X32Y2 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Then Min1+2+3+2Y1+3Y2+(51)X11+(42)X21+(93)X31+(71)X12+(82)X22+(33)X32s.tX11,X21,X31Y1X12,X22,X32Y2 - Let Step-Size =iter=0.85iter1, and 1=2 - \( t_{i t e r}=\frac{\alpha_{\text {iter }}\left(Z_{\text {best_upper }}-Z_{\text {lower(iter })} ight)}{\sum_{i}\left[\sum_{j} X_{i j}-1 ight]^{2}} \) - i(iter)=i(iter1)+titer[1jXij]i 1. 1=2 2. 1=2=3=0 3. Then Lower-Bound Z=Min0+0+0+2Y1+3Y2+(50)X11+(40)X21+(90)X31+(70)X12+(80)X22+(30)X32s.tX11,X21,X31Y1X12,X22,X32Y2 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 1 4- The optimal solution for the Lower-Bound is ZLB=0 5- Come-up with an Upper-bound feasible Solution, Let Then ZUB=20 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 2 1. 2=0.852=1.7 2. t2=i[[jxij1]22(zbestupperzlower(iter))=(100)2+(100)2+(100)21.7(200)=11.333 3. i(iter)=i(iter1)+titer[1jXij]i(2)=i(1)+t2[1jXij] a. 1(2)=0+11.333[100]=11.333 b. 1(2)=0+11.333[100]=11.333 c. 1(2)=0+11.333[100]=11.333 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 2 4Then Lower-Bound Z=Min11.333+11.333+11.333+2Y1+3Y2+(511.333)X11+(411.333)X21+(911.333)X31+(711.333)X12+(811.333)X22+(311.333)X32s.tX11,X21,X31Y1 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 2 4- The optimal solution for the Lower-Bound is ZLB=7 5- Come-up with an Upper-bound feasible Solution, Let Then ZUB=17 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 3 1. 3=0.851.7=1.445 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 2 4- Then Lower-Bound Z=Min6.5166+6.5166+6.5166+2Y1+3Y2+(56.5166)X11+(46.5166)X21+(96.5166)X31+(76.5166)X12+(86.5166)X22+(36.5166)X32s.tX11,X21,X31Y1 NETWORK OPTIMIZATION MODELS Solution using Lagrange relaxation: Iteration 2 4- The optimal solution for the Lower-Bound is ZLB=17 5- Come-up with an Upper-bound feasible Solution, Let Then ZUB=17