I will give thumbs up to the answers please let me know if any questions come up

A. the maximum profit path problem (MPPPath) is presented below. That's where you are given an nxn board with each square having a positive integer profit. Please implement the algorithm described below.

Please see the documents "Dynamic program max profit path problem (MPPP)", a PDF document, and "Dynamic programming MPPP algorithms", a text file(that will be in screenshots below).

Read the values for the p table from a file called ptable.txt. They will be in a file where the first value will be the size of the board and the remaining values will be the valus of p row by row. All values are separated by whitespace. For example, with the data presented in the above PDF document, the file will look like:

5 4 8 2 3 5 2 7 5 10 2 3 2 7 7 9 6 5 7 7 9 8 7 5 9 8 

After doing that we need to add the maximum profit path

We know that each step moves from one row to the next so all we need to know for each row the number of the column for that path. In other words, we need to create a list of n column numbers. This will require another table which we will call d (for direction).

Please see the notes to see how to find this path. In this assignment, called mppath.py or MPPath.java I want you to print the maximum profit, which is the largest value on the last row of the q table and print the maximum profit and the rows and columns of that path from row 1 to row n. Once agan, write the program so that it takes as input a file called ptable.txt. The correct output and the format I want you to use is the following:

C:\>java MPPP The maximum profit is 42. The maximum profit path is: (1,5) (2,4) (3,5) (4,5) (5,4) 

or

C:\>python mppp.py

The maximum profit is 42. The maximum profit path is: (1,5) (2,4) (3,5) (4,5) (5,4)

As before, the program must be written so that it can be run from the command line.

Here are the documents "Dynamic program max profit path problem (MPPP)", a PDF document, and "Dynamic programming MPPP algorithms":

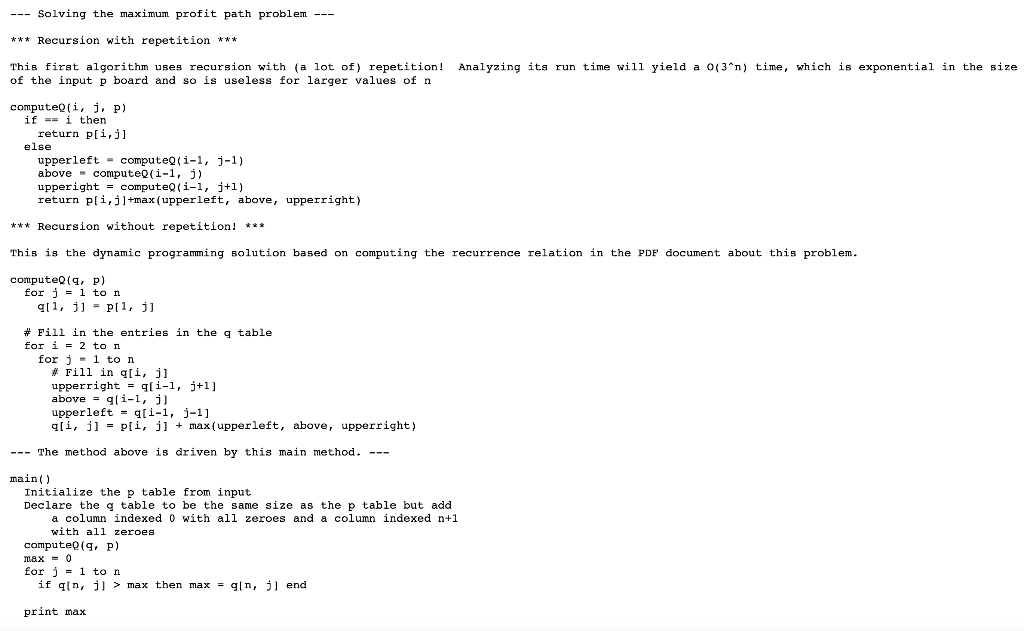
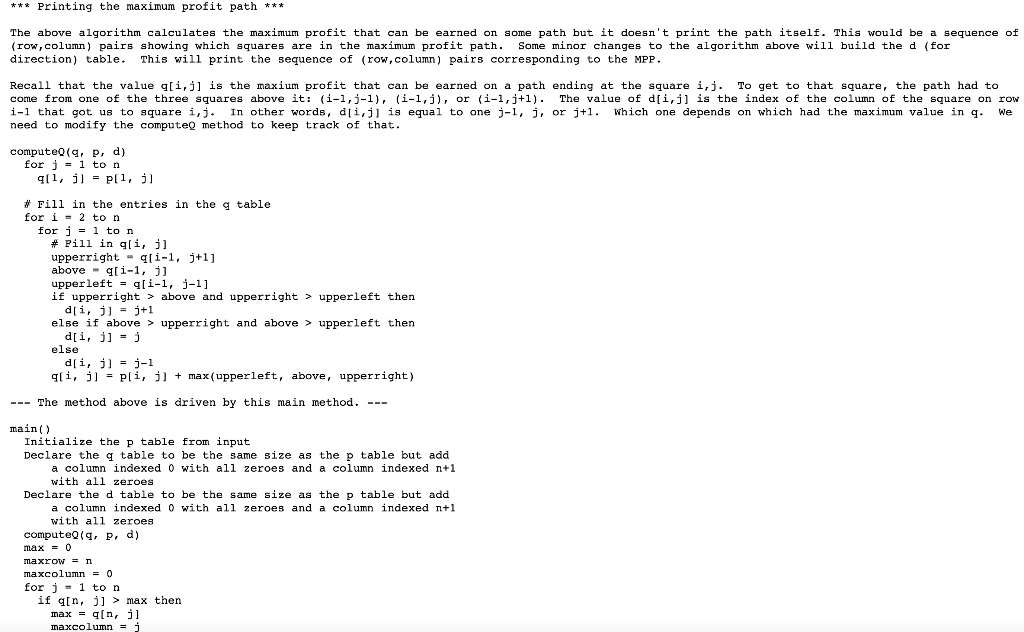
First problem to solve with dynamic programming A maximum-profit path problem Given a 5x5 table where each square has a profit. The problem is to move from the top row down to the bottom row. You can start at any top square. On each move, you can step down to the next row but only to a square that is diagonally to the left, immediately below, or diagonally to the right. You can't step off the board. As you move to each square, you get the profit stored there added to your total. The path ends when you reach a square on the bottom row. The question is: Which of the many paths from a top square to a bottom square will get you the maximum profit? The description above completes step 1(a) from section 3.4. We have described the problem in enough detail to proceed. How do we solve this? We could try every path and record each one's total profit in a list and then search that list for the highest profit. How any paths are there? At each square along a path, there are 2 or 3 squares that could be the next step. Overestimating slightly, let's say that there are 3 choices for every square. On an n x n board, a path contains n squares. Only the last square has no choices because the path stops there. So a path contains n - 1 squares at which 3 choices may be made. This means there are 0 (3n-1) paths. An efficient algorithm cannot try all paths and find the best! To get a better understanding of the problem, here is an example of a 5 x 5 profit board p and a filled-out table q where q[i,j] is maximum profit that can be earned on a path ending at that square. Profit (p table) 1 4 5 5 2 7 p 1 2 3 4 5 2 N||| 3 2 5 7 7 5 4 3 10 7 7 3 9 6 9 8 9 8 Maximum profit from the top to that square (q table) 2 4 5 q 1 2 8 5 3 2 13 22 29 15 17 7 3 15 22 31 42 18 24 24 4 27 33 41 5 35 36 36 So the sub-problem to be solved for each square is to compute the maximum profit one can earn ending at that square. The formula for finding that is given by this recurrence relation. The values in q table were computed using it. p[i,j] if i = 1 q[i,j] (q[i 1,j 1)) q[i 1,j] + p[i,j] otherwise (q[i 1,j + 1]) max So the square at i, j has a value computed by adding p[i,j] to the maximum value among: the square one above and to the left (q[i 1,j 1]) the square directly above (q[i 1,j]) the square one above and to the right (q[i 1,j + 1]) If there is no square because one of the indices is less than 1 or greater than 5, the value used is 0. This completes step 1(b) from section 3.4 in that we now have a formula for filling the q table. Once filled, we scan the bottom row (row 5 in this case) for the largest value. That is the maximum profit one can earn. So now we know where the path must end up. But we don't know what the rest of the path is. We'll take a look at finding that later. --- Solving the maximum profit path problem --- *** Recursion with repetition *** This first algorithm uses recursion with a lot of) repetition! Analyzing its run time will yield a 0(3n) time, which is exponential in the size of the input p board and so is useless for larger values of n computeQ(i, , p) if - i then return p[i,j] else upperleft - computeQ(i-1, j-1) above - computeQ(i-1, j) upperight = computeQ(i-1, j+1) return p[i,j]+max (upperleft, above, upperright) *** Recursion without repetition! *** This is the dynamic programming solution based on computing the recurrence relation in the PDF document about this problem. computevig, p) for j = 1 ton 911, j] = pll, j] # Fill in the entries in the g table for i = 2 ton for j - 1 ton # Fill in a[i, j] upperright = qli-1, j+1] above - q[i-1, j) upperleft = q[i-1, j-1] q[i, j] = p[i, j] + max(upperleft, above, upperright) --- The method above is driven by this main method. --- main() Initialize the p table from input Declare the a table to be the same size as the p table but add a column indexed 0 with all zeroes and a column indexed n+1 with all zeroes compute(9. P) max = 0 for j = 1 ton if qin, il > max then max = qin, il end print max *** Printing the maximum profit path *** The above algorithm calculates the maximum profit that can be earned on some path but it doesn't print the path itself. This would be a sequence of (row,column) pairs showing which squares are in the maximum profit path. Some minor changes to the algorithm above will build the d (for direction) table. This will print the sequence of (row,column) pairs corresponding to the MPP. We Recall that the value a[i,j] is the maxium profit that can be earned on a path ending at the square i,j. To get to that square, the path had to come from one of the three squares above it: (i-1,j-1), (i-1,j), or (i-1,j+1). The value of d[i,j] is the index of the column of the square on row i-l that got us to square i,j. In other words, d[i,jis equal to one j-1, j, or j+1. Which one depends on which had the maximum value in q. need to modify the computeg method to keep track of that. computevig, P. d) for j = 1 to n 911, il = p[i, j] # Fill in the entries in the g table for i = 2 ton for i = 1 ton # Pill in q[i, j] upperright ali-1, j+1] above - q[i-1, j] upperleft = g(i-1, j-1] if upperright > above and upperright > upperleft then d[i, j] = 1+1 else if above > upperright and above > upperleft then d[i, j] = 1 else d[i, j] = 3-1 q[i, j] = pli, j] + max(upperleft, above, upperright) --- The method above is driven by this main method. --- main() Initialize the p table from input Declare the q table to be the same size as the p table but add a column indexed O with all zeroes and a column indexed n+1 with all zeroes Declare the d table to be the same size as the p table but add a column indexed with all zeroes and a column indexed 1+1 with all zeroes computevig, P, d) max = 0 maxrow = n maxcolumn = 0 for j = 1 ton if an, )) > max then max = a[n, il maxcolumn = j main() Initialize the p table from input Declare the q table to be the same size as the p table but add a column indexed 0 with all zeroes and a column indexed n+1 with all zeroes Declare the d table to be the same size as the p table but add a column indexed 0 with all zeroes and a column indexed n+1 with all zeroes computeQ(q, p, d) max = 0 maxrow = n maxcolumn = 0 for j = 1 ton if an, j] > max then max = a[n, j] maxcolumn = j print max printPath(d, maxcolumn) The method printPath has been added. Here it is in pseudocode. printPath(d, maxcolumn) s = new stack column = maxcolumn for row = n downto 1 push column onto stack column = d[row, column] for row = 1 ton column = pop from s print row, column