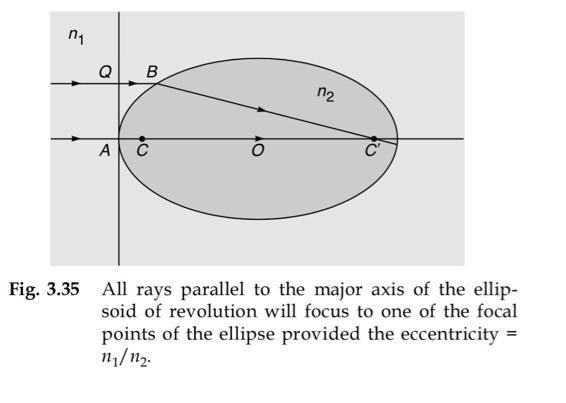
If we rotate an ellipse about its major axis, we obtain what is known as an ellipsoid of revolution. Show by using Fermat's principle that all rays parallel to the major axis of the ellipse will focus to one of the focal points of the ellipse (see Fig. 3.35), provided the eccentricity of the ellipse equals n,/n2. [Hint: Start with the condition that N2AC = nQB + nBC and show that the point B (whose coordinates are x and y) lies on the periphery of an ellipse.] Q. B n2 A Fig. 3.35 All rays parallel to the major axis of the ellip- soid of revolution will focus to one of the focal points of the ellipse provided the eccentricity =