If you could help write the codes thank you
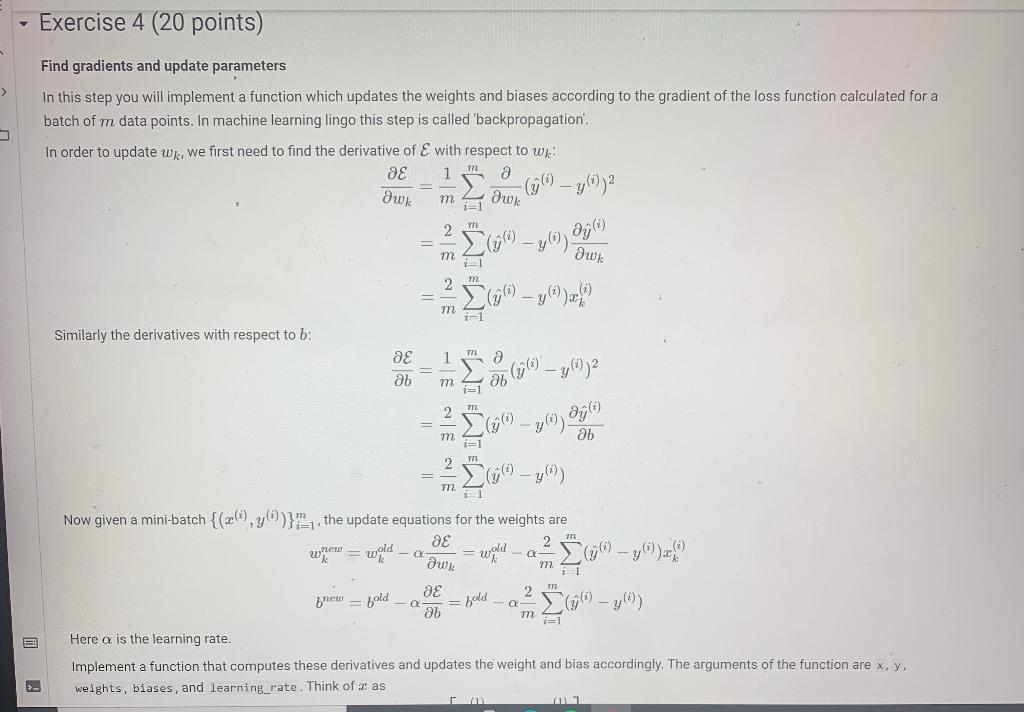
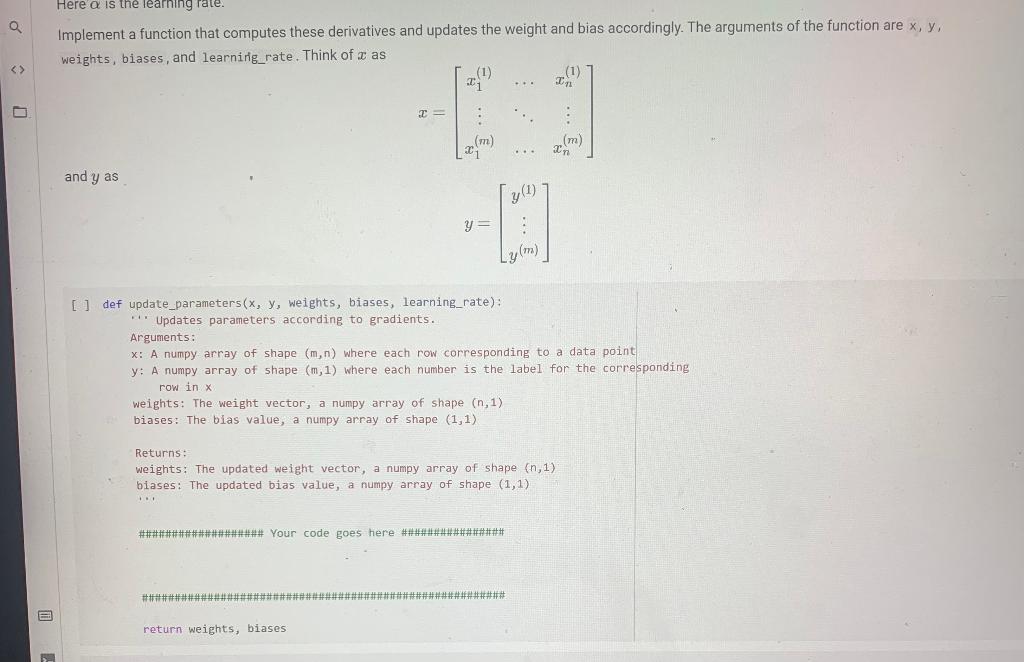
Exercise 4 (20 points) > Find gradients and update parameters In this step you will implement a function which updates the weights and biases according to the gradient of the loss function calculated for a batch of m data points. In machine learning lingo this step is called 'backpropagation'. In order to update wx, we first need to find the derivative of E with respect to w as 1m a awy . aw - y))2 m 2 ay (0 72 -1 Similarly the derivatives with respect to b: 1 a ae ab () - g (6) 2 m = yl) ab 2 771 y) mi 771 we = m Now given a mini-batch {(z), y)}the update equations for the weights are 2 wald = wild m1 2 brew = bold (96) y ab m Here a is the learning rate. Implement a function that computes these derivatives and updates the weight and bias accordingly. The arguments of the function are x, y, weights, biases, and learning rate. Think of as - bold Here a is the learning rate. Implement a function that computes these derivatives and updates the weight and bias accordingly. The arguments of the function are x, y, weights, biases, and learning_rate. Think of as In 2 (m) (m) 2 and y as y = Lym) [ ] def update_parameters (x, y, weights, biases, learning_rate): * Updates parameters according to gradients. Arguments: X: A numpy array of shape (m,n) where each row corresponding to a data point y: A numpy array of shape (m, 1) where each number is the label for the corresponding row in x weights: The weight vector, a numpy array of shape (n,1) biases: The bias value, a numpy array of shape (1,1) Returns: weights: The updated weight vector, a numpy array of shape (n,1) biases: The updated bias value, a numpy array of shape (1,1) ##############****# Your code goes here #*****########### return weights, biases Exercise 4 (20 points) > Find gradients and update parameters In this step you will implement a function which updates the weights and biases according to the gradient of the loss function calculated for a batch of m data points. In machine learning lingo this step is called 'backpropagation'. In order to update wx, we first need to find the derivative of E with respect to w as 1m a awy . aw - y))2 m 2 ay (0 72 -1 Similarly the derivatives with respect to b: 1 a ae ab () - g (6) 2 m = yl) ab 2 771 y) mi 771 we = m Now given a mini-batch {(z), y)}the update equations for the weights are 2 wald = wild m1 2 brew = bold (96) y ab m Here a is the learning rate. Implement a function that computes these derivatives and updates the weight and bias accordingly. The arguments of the function are x, y, weights, biases, and learning rate. Think of as - bold Here a is the learning rate. Implement a function that computes these derivatives and updates the weight and bias accordingly. The arguments of the function are x, y, weights, biases, and learning_rate. Think of as In 2 (m) (m) 2 and y as y = Lym) [ ] def update_parameters (x, y, weights, biases, learning_rate): * Updates parameters according to gradients. Arguments: X: A numpy array of shape (m,n) where each row corresponding to a data point y: A numpy array of shape (m, 1) where each number is the label for the corresponding row in x weights: The weight vector, a numpy array of shape (n,1) biases: The bias value, a numpy array of shape (1,1) Returns: weights: The updated weight vector, a numpy array of shape (n,1) biases: The updated bias value, a numpy array of shape (1,1) ##############****# Your code goes here #*****########### return weights, biases








