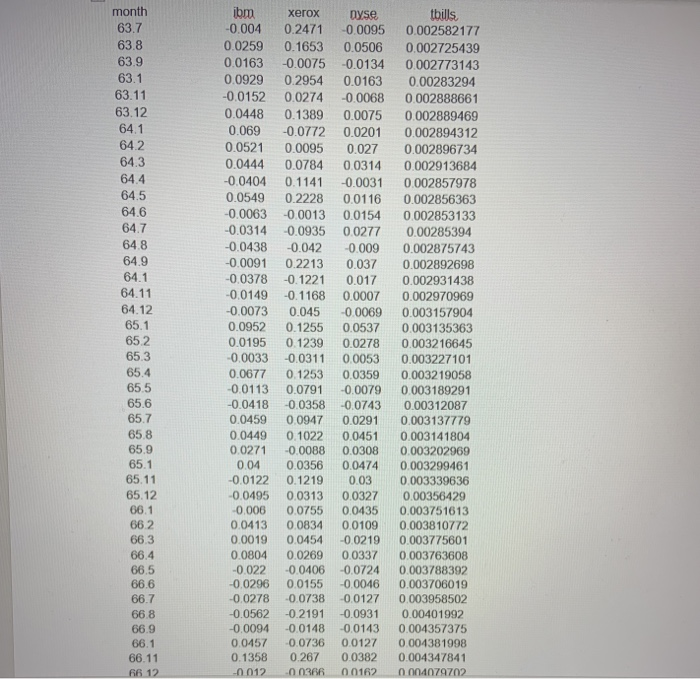
II- From the finance theory, the Capital Asset pricing Model postulates a relationship between the returns on a particular stock and the market return" according to the following model: E(R, -"A)= B,E(RmrA) +u, , Where: R = Return on asset i, R = Return on the market as a whole, TA = The risk-free rate of return. An asset's risk premium is the excess of its return over the risk-free rate, therefore this equation relates the risk premium of asset i to the risk premium on the market. Assets having risk premia that fluctuate less than one-for-one with the market are called defensive assets, and those whose risk premia fluctuate more than one-for-one with the market are called aggressive assets. 1. Use the data provided to you here below to estimate the CAPM model for Xerox, including an intercept. i.e. a model specified as follows: E(R, -rx)= Be + B.E(R. -")+u, 2. Is Xerox best described as a defensive, neutral, or aggressive stock? Is your conclusion statistically significant? (use a 5% significance level) 3. The CAPM suggests that securities having more systematic risk than the market should typically also earn a higher risk premium than the market, and vice versa. Considering your estimate of beta and your sample average risk premia, is it true for Xerox? 4. Are your slope and intercept estimates statistically significant (also at 5%)? What implication(s) can you make from your test conclusions? 5. From your regression results, what proportion of the total variability of the Xerox risk premium is attributable to systematic risk? ibm -0.004 0.0259 0.0163 0.0929 -0.0152 0.0448 0.069 month 63.7 63.8 63.9 63.1 63.11 63.12 64.1 642 64.3 64.4 64.5 64.6 64.7 648 64.9 64.1 64.11 64.12 65.1 652 65.3 65.4 65.5 65.6 65.7 65.8 65.9 65.1 65.11 65.12 66.1 66.2 66.3 66.4 66.5 66.6 66.7 66.8 66.9 66.1 66.11 66 12 0.0444 -0.0404 0.0549 -0.0063 -0.0314 -0.0438 -0.0091 -0.0378 -0.0149 -0.0073 0.0952 0.0195 -0.0033 0.0677 -0.0113 -0.0418 0.0459 0.0449 0.0271 0.04 -0.0122 -0.0495 -0.006 0.0413 0.0019 0.0804 -0.022 -0.0296 -0.0278 -0.0562 -0.0094 0.0457 0.1358 -0012 xerox Dyse thills 0.2471 0.0095 0.002582177 0.1653 0.0506 0.002725439 -0.0075 -0.0134 0.002773143 0.2954 0.0163 0.00283294 0.0274 -0.0068 0.002888661 0.1389 0.0075 0.002889469 -0.0772 0.0201 0.002894312 0.002896734 0.0784 0.0314 0.002913684 0.1141 -0.0031 0.002857978 0.2228 0.0116 0.002856363 0.0013 0.0154 0.002853133 0.0935 0.0277 0.00285394 -0.042 0.0090.002875743 0.2213 0.037 0.002892698 0.1221 0.017 0.002931438 0.1168 0.0007 0.002970969 0.045 0.0069 0.003157904 0.1255 0.0537 0.003135363 0.1239 0.0278 0.003216645 0.0311 0.0053 0.003227101 0.1253 0.035 0.003219058 0.0791 0.0079 0.003189291 0.0358 -0.0743 0.00312087 0.0947 0.0291 0.003137779 0.1022 0.0451 0.003141804 -0.0088 0.0308 0.003202969 0.0356 0.0474 0.003299461 0.1219 0.03 0.003339636 0.0313 0.0327 0.00356429 0.0755 0.0435 0.003751613 0.0834 0.0109 0.003810772 0.0454 -0.0219 0.003775601 0.0269 0.0337 0.003763608 -0.0406 -0.0724 0.003788392 0.0155 -0.0046 0.003706019 0.0738 0.0127 0.003958502 -0.2191 0.0931 0.00401992 -0.0148 -0.0143 0.004357375 0.0736 0.0127 0.004381998 0.267 0.0382 0.004347841 0.0366 00162 0004079702 II- From the finance theory, the Capital Asset pricing Model postulates a relationship between the returns on a particular stock and the market return" according to the following model: E(R, -"A)= B,E(RmrA) +u, , Where: R = Return on asset i, R = Return on the market as a whole, TA = The risk-free rate of return. An asset's risk premium is the excess of its return over the risk-free rate, therefore this equation relates the risk premium of asset i to the risk premium on the market. Assets having risk premia that fluctuate less than one-for-one with the market are called defensive assets, and those whose risk premia fluctuate more than one-for-one with the market are called aggressive assets. 1. Use the data provided to you here below to estimate the CAPM model for Xerox, including an intercept. i.e. a model specified as follows: E(R, -rx)= Be + B.E(R. -")+u, 2. Is Xerox best described as a defensive, neutral, or aggressive stock? Is your conclusion statistically significant? (use a 5% significance level) 3. The CAPM suggests that securities having more systematic risk than the market should typically also earn a higher risk premium than the market, and vice versa. Considering your estimate of beta and your sample average risk premia, is it true for Xerox? 4. Are your slope and intercept estimates statistically significant (also at 5%)? What implication(s) can you make from your test conclusions? 5. From your regression results, what proportion of the total variability of the Xerox risk premium is attributable to systematic risk? ibm -0.004 0.0259 0.0163 0.0929 -0.0152 0.0448 0.069 month 63.7 63.8 63.9 63.1 63.11 63.12 64.1 642 64.3 64.4 64.5 64.6 64.7 648 64.9 64.1 64.11 64.12 65.1 652 65.3 65.4 65.5 65.6 65.7 65.8 65.9 65.1 65.11 65.12 66.1 66.2 66.3 66.4 66.5 66.6 66.7 66.8 66.9 66.1 66.11 66 12 0.0444 -0.0404 0.0549 -0.0063 -0.0314 -0.0438 -0.0091 -0.0378 -0.0149 -0.0073 0.0952 0.0195 -0.0033 0.0677 -0.0113 -0.0418 0.0459 0.0449 0.0271 0.04 -0.0122 -0.0495 -0.006 0.0413 0.0019 0.0804 -0.022 -0.0296 -0.0278 -0.0562 -0.0094 0.0457 0.1358 -0012 xerox Dyse thills 0.2471 0.0095 0.002582177 0.1653 0.0506 0.002725439 -0.0075 -0.0134 0.002773143 0.2954 0.0163 0.00283294 0.0274 -0.0068 0.002888661 0.1389 0.0075 0.002889469 -0.0772 0.0201 0.002894312 0.002896734 0.0784 0.0314 0.002913684 0.1141 -0.0031 0.002857978 0.2228 0.0116 0.002856363 0.0013 0.0154 0.002853133 0.0935 0.0277 0.00285394 -0.042 0.0090.002875743 0.2213 0.037 0.002892698 0.1221 0.017 0.002931438 0.1168 0.0007 0.002970969 0.045 0.0069 0.003157904 0.1255 0.0537 0.003135363 0.1239 0.0278 0.003216645 0.0311 0.0053 0.003227101 0.1253 0.035 0.003219058 0.0791 0.0079 0.003189291 0.0358 -0.0743 0.00312087 0.0947 0.0291 0.003137779 0.1022 0.0451 0.003141804 -0.0088 0.0308 0.003202969 0.0356 0.0474 0.003299461 0.1219 0.03 0.003339636 0.0313 0.0327 0.00356429 0.0755 0.0435 0.003751613 0.0834 0.0109 0.003810772 0.0454 -0.0219 0.003775601 0.0269 0.0337 0.003763608 -0.0406 -0.0724 0.003788392 0.0155 -0.0046 0.003706019 0.0738 0.0127 0.003958502 -0.2191 0.0931 0.00401992 -0.0148 -0.0143 0.004357375 0.0736 0.0127 0.004381998 0.267 0.0382 0.004347841 0.0366 00162 0004079702