Imagining With The 4f System. Consider The 4f Optical System Shown In The Figure Below Which Consists Of Two Lenses With Focal Lengths Of Fi And F2. A Mask With The Transmittance Of T(X, Y) Is Placed At The Back Focal Plane Of The Lens I. The Wave Function Of Light Of Wavelength ? Which Is Incident From Left Is U- F(X,Y) At The Front Focal Plane Of The Lens

 

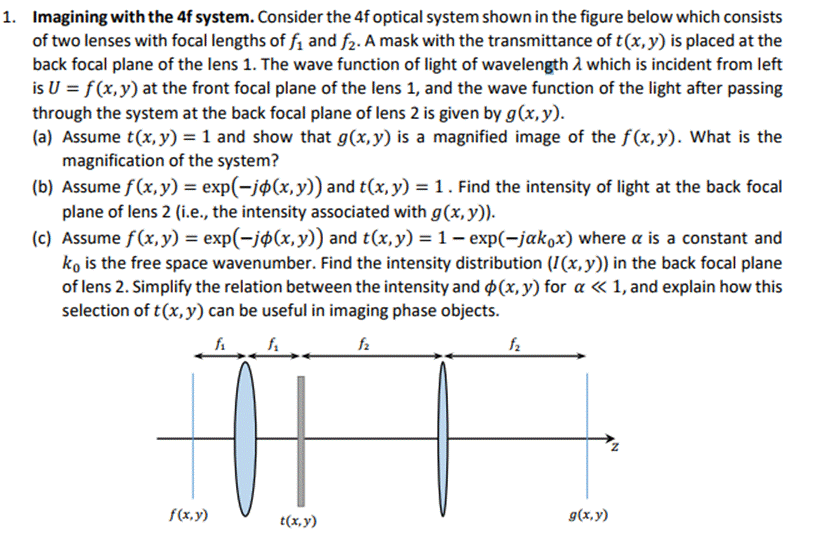
1. Imagining with the 4f system. Consider the 4f optical system shown in the figure below which consists of two lenses with focal lengths of f and f. A mask with the transmittance of t(x, y) is placed at the back focal plane of the lens 1. The wave function of light of wavelength which is incident from left is U = f(x,y) at the front focal plane of the lens 1, and the wave function of the light after passing through the system at the back focal plane of lens 2 is given by g(x, y). (a) Assume t(x, y) = 1 and show that g(x,y) is a magnified image of the f(x,y). What is the magnification of the system? (b) Assume f(x, y) = exp(-j(x, y)) and t(x, y) = 1. Find the intensity of light at the back focal plane of lens 2 (i.e., the intensity associated with g(x, y)). (c) Assume f(x, y) = exp(-j(x, y)) and t(x, y) = 1 - exp(-jakox) where a is a constant and ko is the free space wavenumber. Find the intensity distribution (I(x, y)) in the back focal plane of lens 2. Simplify the relation between the intensity and (x, y) for a < < 1, and explain how this selection of t(x, y) can be useful in imaging phase objects. fi fi fz fz f(x,y) t(x,y) g(x,y)