Implement algorithm using matlab
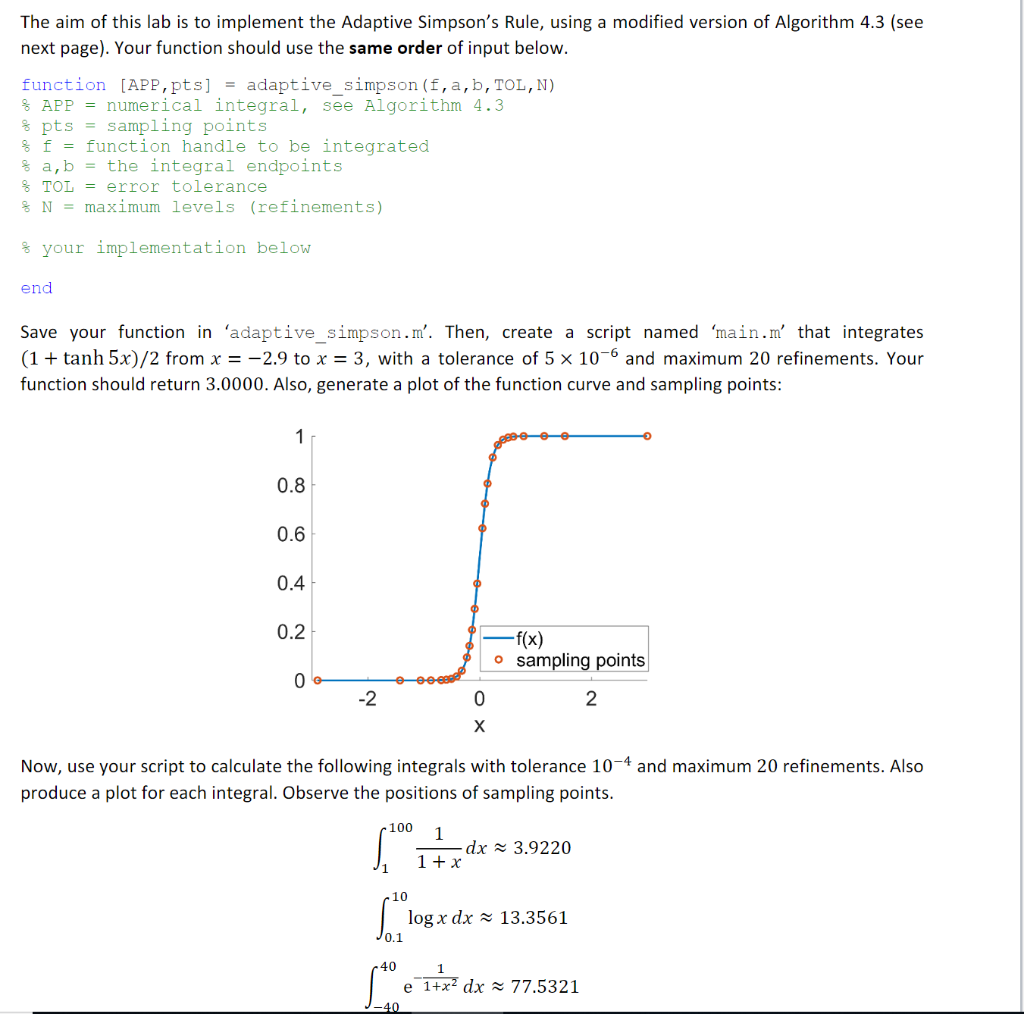



The aim of this lab is to implement the Adaptive Simpson's Rule, using a modified version of Algorithm 4.3 (see next page). Your function should use the same order of input below function [APP,pts] = adaptive-simpson ( f , a,b, TOL,N) % APP numerical integral, see Algorithm 4.3 % pts sampling points % f function handle to be integrated % a,b = the integral endpoints % TOL error tolerance % N = maximum levels (refinements) % your implementation below end Save your function in adaptive-simpson . m. Then, create a script named man.m, that integrates (1 + tanh 5x)/2 from x =-2.9 to x 3, with a tolerance of 5 x 10-6 and maximum 20 refinements. Your function should return 3.0000. Also, generate a plot of the function curve and sampling points 0.8 0.6 0.4 0.2 0 f(x) o sampling points -2 2 Now, use your script to calculate the following integrals with tolerance 10-4 and maximum 20 refinements. Alsa produce a plot for each integral. Observe the positions of sampling points 100 1 + x 10 logx dx ~ 13.3561 40 e1+x dx 77.5321 Modified Adaptive Simpson's rule To approximate the integral f(x) dx to within a given tolerance: INPUT endpoints a, b; tolerance TOL; limit N to number of levels. OUTPUT approximation APP or message that N is exceeded. And sampling points, pts. Step 1 Set APP=0; TOLi = 10 TOL. hi = (b-a) /2; FAi-f(a); FG = f(a + hi): FBf (b); S,-hi (FA +4FCi FB)/3 (Approximation from Simpson's method for entire interval.) pts [a, bl Step 2 While i 0 do Steps 3-5. Step 3 Set FD-f(ai h/2); FE = f(ait3hi/2); S1 -hi(FAi +4FD + FCi)/6; (Approximations from Simpson's method for halves of subintervals.) v1 = ai; (Save data at this level.) V5 = hi; Step 4 Set ii -1. (Delete the level.) Step 5 If IS1 S2 7l v6 then set APP APP(S1S2) else if (vs 2 N) then OUTPUT ('LEVEL EXCEEDED): (Procedure fails.) STOP (Add one level.) set i=i+1; else (Data for right-half subinterval.) FG = FE. FBi = U4; hi = us/2: TOLi = V612; Si = S2; pts = [pts. ai]; (Data for left-half subinterval.) set i=i+ 1; FA = 2. hi = hi-1; Li = Li-1. pts = [pts. ai]; Step 6 OUTPUT (APP) (APP approximates I to within TOL.) STOP. The aim of this lab is to implement the Adaptive Simpson's Rule, using a modified version of Algorithm 4.3 (see next page). Your function should use the same order of input below function [APP,pts] = adaptive-simpson ( f , a,b, TOL,N) % APP numerical integral, see Algorithm 4.3 % pts sampling points % f function handle to be integrated % a,b = the integral endpoints % TOL error tolerance % N = maximum levels (refinements) % your implementation below end Save your function in adaptive-simpson . m. Then, create a script named man.m, that integrates (1 + tanh 5x)/2 from x =-2.9 to x 3, with a tolerance of 5 x 10-6 and maximum 20 refinements. Your function should return 3.0000. Also, generate a plot of the function curve and sampling points 0.8 0.6 0.4 0.2 0 f(x) o sampling points -2 2 Now, use your script to calculate the following integrals with tolerance 10-4 and maximum 20 refinements. Alsa produce a plot for each integral. Observe the positions of sampling points 100 1 + x 10 logx dx ~ 13.3561 40 e1+x dx 77.5321 Modified Adaptive Simpson's rule To approximate the integral f(x) dx to within a given tolerance: INPUT endpoints a, b; tolerance TOL; limit N to number of levels. OUTPUT approximation APP or message that N is exceeded. And sampling points, pts. Step 1 Set APP=0; TOLi = 10 TOL. hi = (b-a) /2; FAi-f(a); FG = f(a + hi): FBf (b); S,-hi (FA +4FCi FB)/3 (Approximation from Simpson's method for entire interval.) pts [a, bl Step 2 While i 0 do Steps 3-5. Step 3 Set FD-f(ai h/2); FE = f(ait3hi/2); S1 -hi(FAi +4FD + FCi)/6; (Approximations from Simpson's method for halves of subintervals.) v1 = ai; (Save data at this level.) V5 = hi; Step 4 Set ii -1. (Delete the level.) Step 5 If IS1 S2 7l v6 then set APP APP(S1S2) else if (vs 2 N) then OUTPUT ('LEVEL EXCEEDED): (Procedure fails.) STOP (Add one level.) set i=i+1; else (Data for right-half subinterval.) FG = FE. FBi = U4; hi = us/2: TOLi = V612; Si = S2; pts = [pts. ai]; (Data for left-half subinterval.) set i=i+ 1; FA = 2. hi = hi-1; Li = Li-1. pts = [pts. ai]; Step 6 OUTPUT (APP) (APP approximates I to within TOL.) STOP










