import quadprog import numpy as np # The helper function. Dot not change it def quadprog_solve_qp(P, q, G=None, h=None, A=None, b=None): qp_G = .5 *

import quadprog import numpy as np

# The helper function. Dot not change it def quadprog_solve_qp(P, q, G=None, h=None, A=None, b=None): qp_G = .5 * (P + P.T) # make sure P is symmetric qp_a = -q if A is not None: qp_C = -np.vstack([A, G]).T qp_b = -np.hstack([b, h]) meq = A.shape[0] else: # no equality constraint qp_C = -G.T qp_b = -h meq = 0 return quadprog.solve_qp(qp_G, qp_a, qp_C, qp_b, meq)[0]

# Toy data X = np.array([ [0, 0], [2, 0], [0, 2], [3, 3], [4, 4] ]) Y = np.array([-1, -1, -1, 1, 1])

image text in transcribed

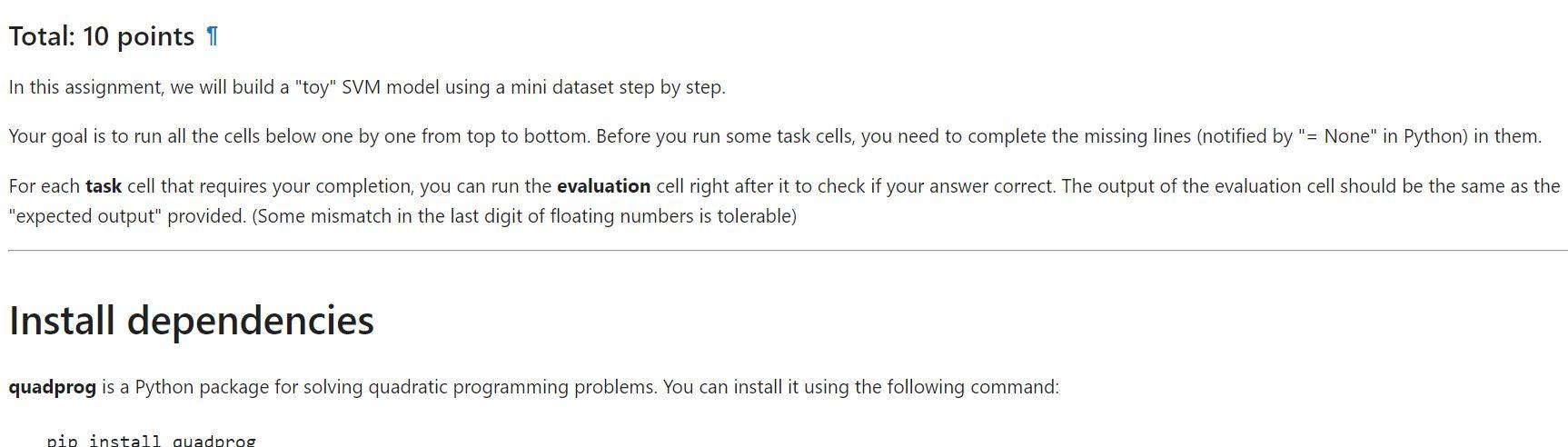
Q = np.zeros((5, 5))

### START YOUR CODE ### for i in range(Q.shape[0]): for j in range(Q.shape[1]): # Use the ith and jth examples in X and Y to compute Q_ij # Hint: Q_ij = y^i * y^j * (x^i @ x^j) Q[i, j] = None ### END YOUR CODE ###

print('Q = ', Q)

image text in transcribed

### START YOUR CODE ### P = Q + np.eye(5)*1e-5 # To solve the non-positive finite issue

# Hint: Use np.ones(), q is of length 5 q = None

# Hint: G is a matrix whose diagnal elements are 1s, and other elements are 0s. Use np.eye() G = None

# Hint: h is of length 5, with all zeros; Use np.zeros() h = None

A = Y.reshape((1,5))

# Hint: b is of length 1, with zero value; Use np.zeros() b = None

### END YOUR CODE ###

print('q = ', q) print('G = ', G) print('h = ', h) print('b = ', b)

image text in transcribed

Total: 10 points In this assignment, we will build a "toy" SVM model using a mini dataset step by step. Your goal is to run all the cells below one by one from top to bottom. Before you run some task cells, you need to complete the missing lines (notified by "= None" in Python) in them. For each task cell that requires your completion, you can run the evaluation cell right after it to check if your answer correct. The output of the evaluation cell should be the same as the "expected output" provided. (Some mismatch in the last digit of floating numbers is tolerable) Install dependencies quadprog is a Python package for solving quadratic programming problems. You can install it using the following command: We want to build an SVM model on the toy dataset: x(1)=(0,0),y(1)=1x(2)=(2,0),y(2)=1x(3)=(0,2),y(3)=1x(4)=(3,3),y(4)=1x(5)=(4,4),y(5)=1 We need to solve the quadratic programming (QP) problem as the following form: min(21TQ(1)T) subject to: yT=0,0 The quadprog package by defaualt solves the QP as this form: minx(21xTPx+qTx) subject to: Gxh,Ax=b Therefore, in order to use quadprog, we need to establish the responding relationships between variables: P=Q,q=(1)T,G=(1)T,h=(0)T,A=yT,b=(0)T Task 1: Compute matrix Q 3 points First, we need to use x(i) and y(i) to compute matrix Q : Q=y(1)y(1)x(1)Tx(1)y(2)y(1)x(2)Tx(1)y(5)y(1)x(5)Tx(1)y(1)y(2)x(1)Tx(2)y(2)y(2)x(2)Tx(2)y(5)y(2)x(5)Tx(2)y(1)y(5)x(1)Tx(5)y(2)y(5)x(2)Tx(5)y(5)y(5)x(5)Tx(5) Expected output Q=[[0.0.0.0.0.0.0][0.4.0.-6.-8.][0.0.4.-6.-8.][0.6.6.18,24.][0.-8.8.24.32.]] 3 points Use the folumas: P=Q,q=(1)T,G=(1)T,h=(0)T,A=yT,b=(0)T \#\#\# START YOUR CODE \#\#\# P=Q+np.eye (5)1e5 \# To solve the non-positive finite issue \# Hint: Use np.ones(), q is of length 5 q= None \# Hint: G is a matrix whose diagnal elements are 1s, and other elements are Os. Use np.eye() G= None \# Hint: h is of length 5, with all zeros; Use np.zeros() h= None A=Yreshape((1,5)) \# Hint: b is of length 1 , with zero value; Use np.zeros() b= None \#\#\# END YOUR CODE \#\#\# print(q= ' q, q) print(G= ' G, G) print(h=,h) print(b=,b) Expected output q=[1.1.1.1.1.]G=[[1.0.0.0.0.][0.1.0.0.0.][0.0.1.0.0.][0.0.0.1.0.][0.0.0.0.1.]]h=[0.0.0.0.0.0.]b=[0.] Task 3: Call quadprog 1 point \#\#\# START YOUR CODE \#\#\# \# Hint: Call quadprog_solve_qp() with the correct arguments solution = None \#\#\# END YOUR CODE \#\#\# print('solution = ', solution) print('The support vectors are: ', X[ solution >,]) Expected output [02] [33]] 3 points Use the support vectors to solve the w and b in the decision boundary wTx+b=0. Use the property that a support vector x(k) must satistify y(k)(wTx(k)+b)=1. You can solve it with a paper and pen by listing linear equations. NOTE: Solve this task on paper. You only need to provide the answers for w1, w2, and b. Hint: You should solve the following linear equations: y(2)(wTx(2)+b)=1y(3)(wTx(3)+b)=1y(4)(wTx(4)+b)=1 \#\#\# START YOUR ANSWERS \#\#\# w1 = None w2 = None b= None \#\# END YOUR ANSWERS print(w1= ',w1) print(w2=,w2)