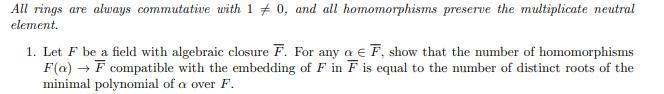
All rings are always commutative with 10, and all homomorphisms preserve the multiplicate neutral element. 1. Let F be a field with algebraic closure F. For any a F. show that the number of homomorphisms F(a) F compatible with the embedding of F in F is equal to the number of distinct roots of the minimal polynomial of a over F.