In java:

First, create a MATRIX-CHAIN-MULTIPLICATION class and include the bottom-up approach class methodsMATRIX-CHAIN-ORDER and PRINT-OPTIMAL-PARENS. The pseudocode for these two algorithms are given below. Also, you will need a recursive method MATRIX-CHAIN-MULTIPLY, as outlined in Exercise 15.2-2.

MATRIX-CHAIN-ORDER and PRINT-OPTIMAL-PARENS:

exercise 15.2-2:

Next, add to the class the top-down approaches RECURSIVE-MATRIX-CHAIN and MEMOIZED-MATRIX- CHAIN together with its helper method LOOKUP-CHAIN. (You may find that you want a method RECURSIVE-CHAIN-MULTIPLY as well. Which codes to write is largely up to you.)

Use a bottom-up approach to compute the product matrix A which is the result of multiplying all of the six input matrices together. Instrument your code so that you can measure the amount of time taken to compute the product matrix A.

Then use a top-down approach to compute the product matrix A using a recursive approach. Again, instrument your code to record the amount of time taken on the top-down recursive approach.

Finally, use the top-down memoized approach to compute the product matrix A and record the time required. Note the absence of the auxiliary array s in the top-down approach.

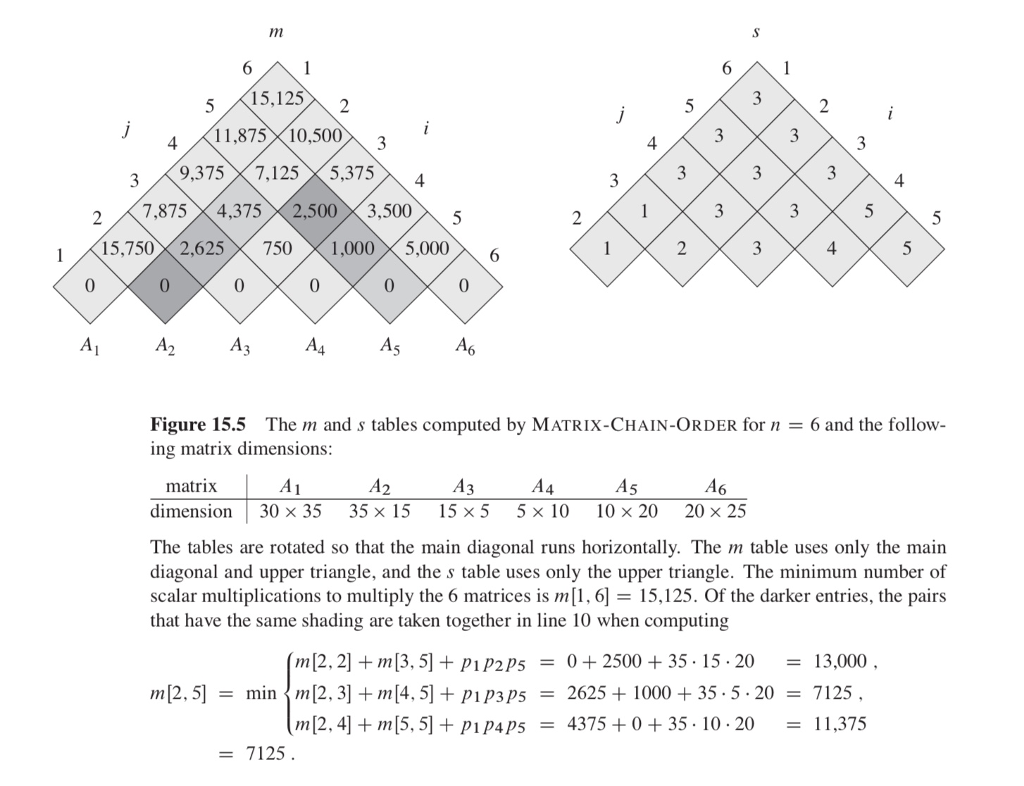
Write a driver program that creates six matrices, A1 through A6 of the dimensions given in the example shown in Figure 15.5. Fill the matrices with random integers on the interval (0, 100).

figure 15.5:

PRINT-OPTIMAL-PARENS(s, i, j) MATRIX-CHAIN-ORDER(p) 1 n = p.length-1 2 let m[1..n, 1..n] and s[1..n-1, 2.n] be new tables2 print "A" i 3 fori-1 to n 3 else print "C" 4 PRINT-OPTIMAL-PARENS(s, ?, s[i,j]) 5 PRINT-OPTIMAL-PARENS(s, s[i,j]+1,j) 5 for l- 2 to n /I I is the chain length 6 for i -1 to n- 1 6 print ") j=i+1-1 8 m[i, j] 9 for k i to j-1 10 q = mli, k] + m[k+1, j] + pi-1 pp, 11 ifq?m[i,j] 12 13 14 return m and s m[i, j] = q sli, jl k PRINT-OPTIMAL-PARENS(s, i, j) MATRIX-CHAIN-ORDER(p) 1 n = p.length-1 2 let m[1..n, 1..n] and s[1..n-1, 2.n] be new tables2 print "A" i 3 fori-1 to n 3 else print "C" 4 PRINT-OPTIMAL-PARENS(s, ?, s[i,j]) 5 PRINT-OPTIMAL-PARENS(s, s[i,j]+1,j) 5 for l- 2 to n /I I is the chain length 6 for i -1 to n- 1 6 print ") j=i+1-1 8 m[i, j] 9 for k i to j-1 10 q = mli, k] + m[k+1, j] + pi-1 pp, 11 ifq?m[i,j] 12 13 14 return m and s m[i, j] = q sli, jl k