IN PYTHON PLEASE

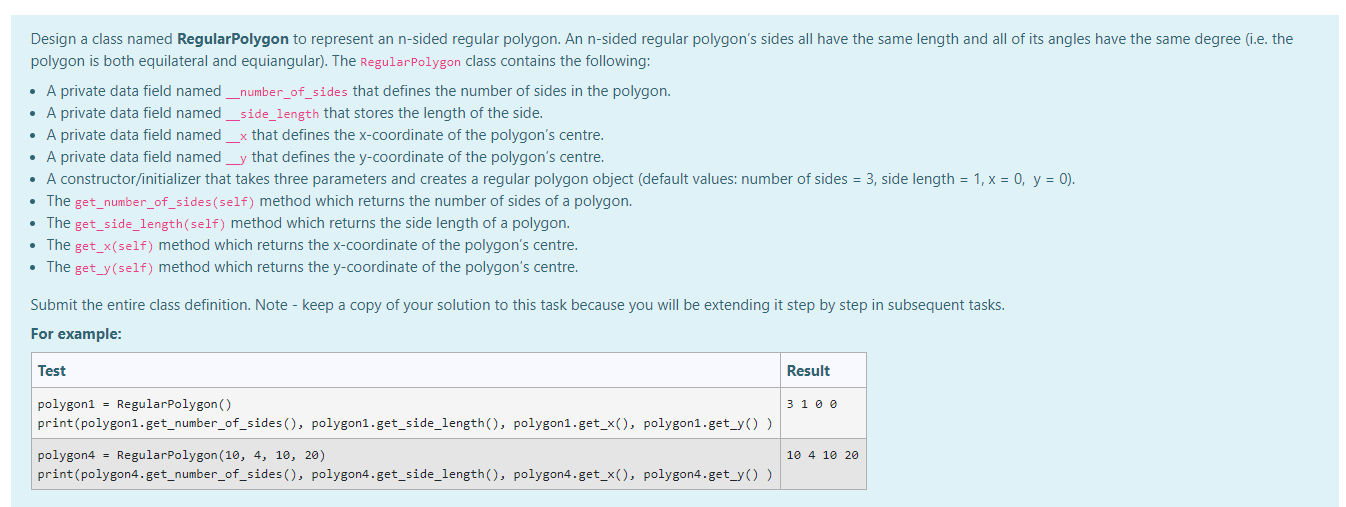
1a

1b

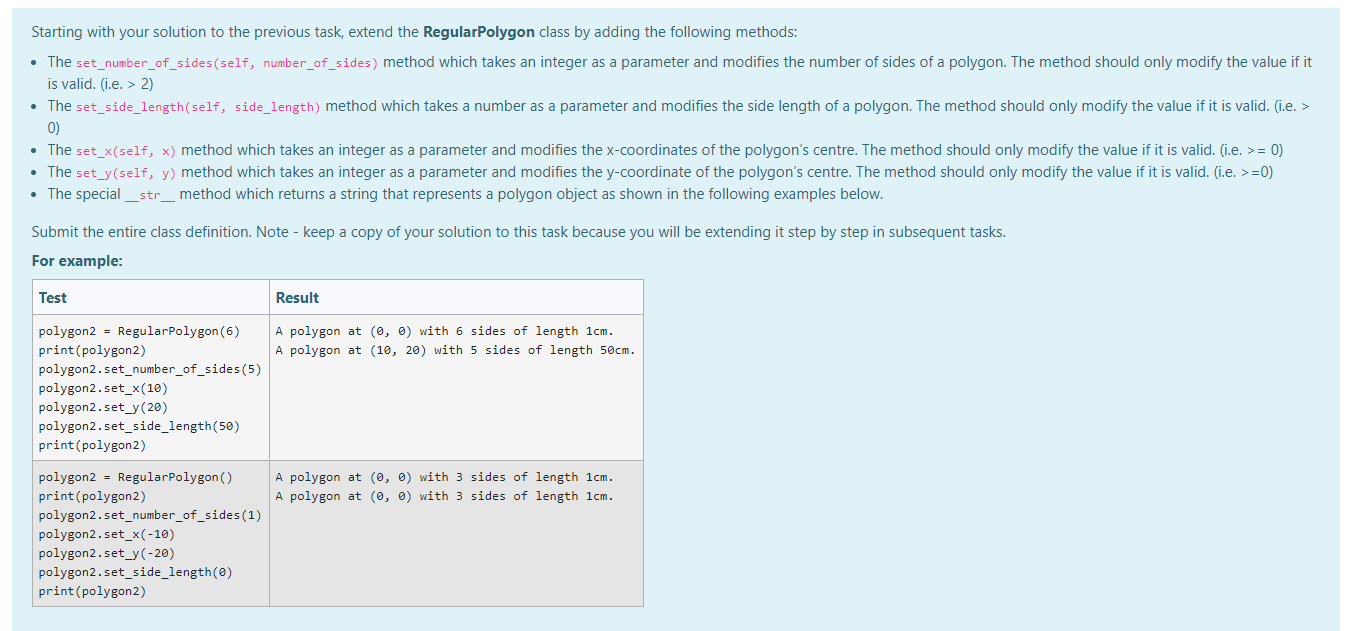
1c

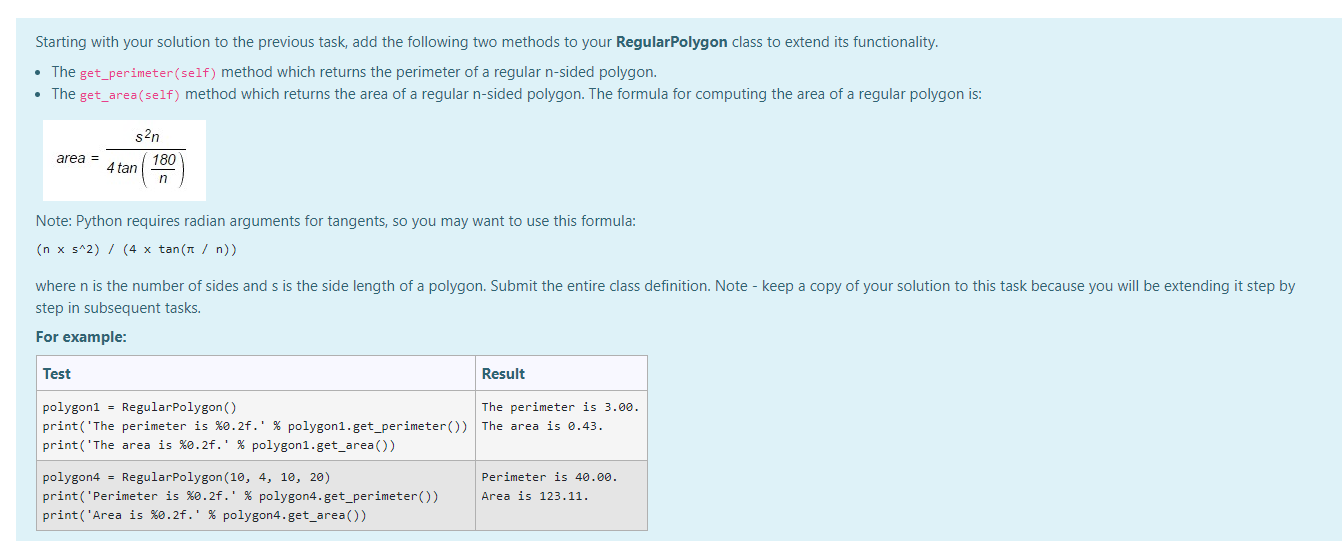
1d

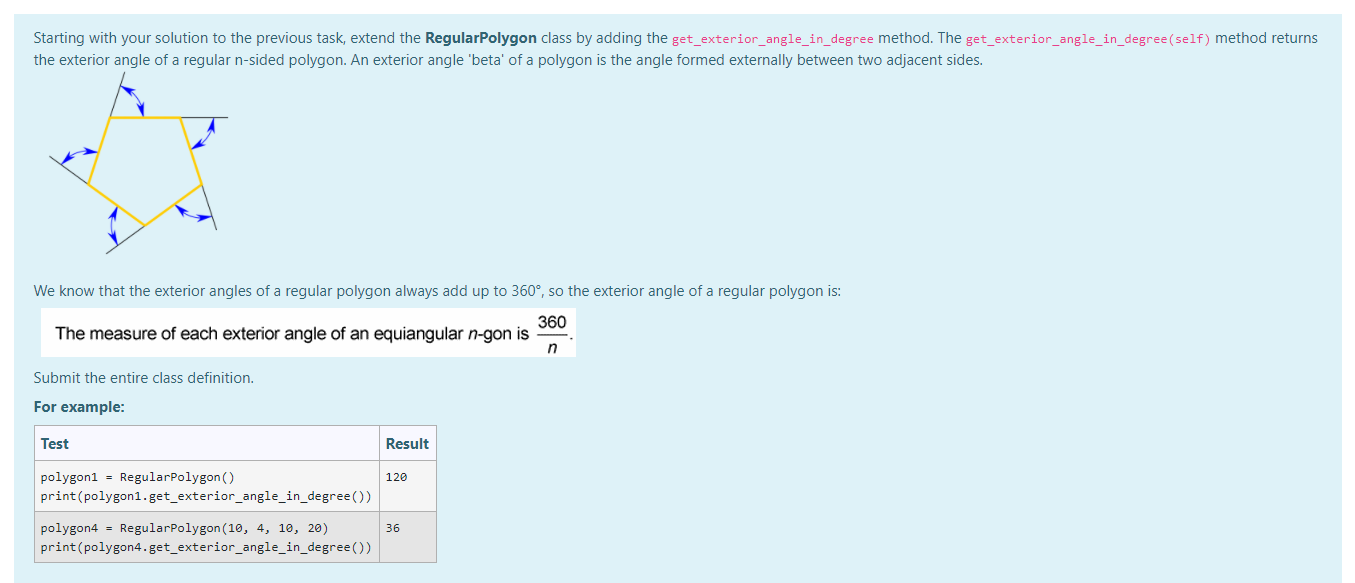Thanks you.

Design a class named RegularPolygon to represent an n-sided regular polygon. An n-sided regular polygon's sides all have the same length and all of its angles have the same degree (i.e. the polygon is both equilateral and equiangular). The RegularPolygon class contains the following: A private data field named _number_of_sides that defines the number of sides in the polygon. A private data field named_side_length that stores the length of the side. A private data field named x that defines the x-coordinate of the polygon's centre. A private data field named that defines the y-coordinate of the polygon's centre. A constructor/initializer that takes three parameters and creates a regular polygon object (default values: number of sides = 3, side length = 1, x = 0, y = 0). The get_number_of_sides (self) method which returns the number of sides of a polygon. The get_side_length(self) method which returns the side length of a polygon. The get_x(self) method which returns the x-coordinate of the polygon's centre. The get_y(self) method which returns the y-coordinate of the polygon's centre. Submit the entire class definition. Note - keep a copy of your solution to this task because you will be extending it step by step in subsequent tasks. For example: Test Result 3 1 0 0 polygon1 = RegularPolygon() print (polygon1.get_number_of_sides(), polygon1.get_side_length(), polygon1.get_x(), polygon1.get_y()) polygon4 = RegularPolygon (10, 4, 10, 20) print(polygon4.get_number_of_sides(), polygon4.get_side_length(), polygon4.get_x(), polygon4.get_y()) 10 4 10 20 Starting with your solution to the previous task, extend the RegularPolygon class by adding the following methods: The set_number_of_sides(self, number_of_sides) method which takes an integer as a parameter and modifies the number of sides of a polygon. The method should only modify the value if it is valid. (.e. > 2) The set_side_length(self, side_length) method which takes a number as a parameter and modifies the side length of a polygon. The method should only modify the value if it is valid. (i..> 0) The set_x(self, x) method which takes an integer as a parameter and modifies the x-coordinates of the polygon's centre. The method should only modify the value if it is valid. (i.e. >= 0) The set_y(self, y) method which takes an integer as a parameter and modifies the y-coordinate of the polygon's centre. The method should only modify the value if it is valid. (i.e. >=0) The special_str_method which returns a string that represents a polygon object as shown in the following examples below. Submit the entire class definition. Note - keep a copy of your solution to this task because you will be extending it step by step in subsequent tasks. For example: Test Result A polygon at (0, 0) with 6 sides of length 1cm. A polygon at (10, 20) with 5 sides of length 50cm. polygon2 = RegularPolygon (6) print(polygon2) polygon2.set_number_of_sides (5) polygon2.set_x(10) polygon2.set_y(20) polygon2.set_side_length(50) print (polygon2) A polygon at (0, 0) with 3 sides of length 1cm. A polygon at (0, 0) with 3 sides of length 1cm. polygon2 = RegularPolygon() print (polygon2) polygon2.set_number_of_sides (1) polygon2.set_x(-10) polygon2.set_y(-20) polygon2.set_side_length() print (polygon2) Starting with your solution to the previous task, add the following two methods to your RegularPolygon class to extend its functionality. The get_perimeter(self) method which returns the perimeter of a regular n-sided polygon. The get_area(self) method which returns the area of a regular n-sided polygon. The formula for computing the area of a regular polygon is: san 180 area = 4 tan Note: Python requires radian arguments for tangents, so you may want to use this formula: (n x s^2) / (4 x tan(n / n)) where n is the number of sides and s is the side length of a polygon. Submit the entire class definition. Note - keep a copy of your solution to this task because you will be extending it step by step in subsequent tasks. For example: Test Result polygon1 = RegularPolygon() The perimeter is 3.00. print('The perimeter is %0.2f.' % polygon1.get_perimeter() The area is 0.43. print('The area is %0.2f.' % polygon1.get_area() polygon4 = RegularPolygon (10, 4, 10, 20) Perimeter is 40.00. print('Perimeter is %0.2f.' % polygon4.get_perimeter() Area is 123.11. print('Area is %0.2f.' % polygon4.get_area() Starting with your solution to the previous task, extend the RegularPolygon class by adding the get_exterior_angle_in_degree method. The get_exterior_angle_in_degree(self) method returns the exterior angle of a regular n-sided polygon. An exterior angle 'beta' of a polygon is the angle formed externally between two adjacent sides. We know that the exterior angles of a regular polygon always add up to 360, so the exterior angle of a regular polygon is: 360 The measure of each exterior angle of an equiangular n-gon is n Submit the entire class definition. For example: Test Result 120 polygon1 = RegularPolygon() print(polygon1.get_exterior_angle_in_degree()) 36 polygon4 = RegularPolygon (10, 4, 10, 20) print (polygon4.get_exterior_angle_in_degree())