In this homework assignment, you will write code to empirically compare the performance of a naive and a fast 2 2 matrix exponentiation method. The naive matrix exponentiation method consists of successive computation of matrix products: mn = Qn i=1 m = m m m m | {z } n times . The fast matrix exponentiation algorithm involves successive squaring. See a description of the algorithm in Listing 1.

Listing 1: A Fast Matrix Exponentiation Algorithm

1 Algorithm fastPower(m,n)

2 Input: a matrix m and n 1 is an integer

3 Output: mn, a matrix

4 result I

5 while n =! 0 do

6 if n mod 2 6= 0 then

7 result result m

8 endif

9 n n div 2

10 if n =! 0 then

11 m m m

12 endif

13 endwhile

14 return result

I in the algorithm denotes the identity matrix: a matrix whose main (top-left to bottom-right) diagonal entries are 1s and all other entries are 0s. This matrix is the matrix multiplicative identity.

Define a class, Mat2By2, that implements the Mat2By2API interface. This class will consist of only one instance variable entries, a reference to a two-dimensional array of BigInteger objects. In addition to the abstract instance methods from the Mat2By2API interface, this class will implement the following constructors:

Listing 2: Default Constructor

1 /**

2 * A default constructor that creates the zero 2x2 matrix

3 */

4 public Mat2By2()

Listing 3: A Parameterized Constructor

1 /**

2 * Creates a 2x2 matrix with the specified entries

3 * @param e11 a BigInteger object representing top-left entry

4 * @param e12 a BigInteger object representing top-right entry

5 * @param e21 a BigInteger object representing bottom-left entry

6 * @param e22 a BigInteger object representing bottom-right entry

7 */

8 public Mat2By2(BigInteger e11,BigInteger e12,BigInteger e21,BigInteger e22- )

Listing 4: A Copy Constructor

1 /**

2 * Creates a 2x2 matrix of BigInteger objects with the sames entries as

3 * the specified matrix

4 * @param m a 2 x 2 matrix of BigInteger objects

5 */

6 public Mat2By2(Mat2By2 m)

The MatrixExponentiationDemo Class Definition 2. The Fibonacci numbers are the sequence of numbers {Fn} n=1 defined by the recurrence equation Fn = Fn1 + Fn2, where F1 = F2 = 1. By convention F0 = 0. The first eight terms of the Fibonacci sequence are 1, 1, 2, 3, 5, 8, 13, 21, .

MatrixExponentiationDemo will contain the main and the following methods:

Listing 5: A Fast Matrix Exponentiation Method

1 /**

2 * Computes the power of the specified matrix by successive squaring

3 * @param m a 2x2 matrix of BigInteger objects

4 * @param n a positive integer representing the exponent

5 * @return the nth power of the specified matrix (m^n)

6 * @throws IllegalArgumentException when n

7 */

8 private static Mat2By2 fastPower(Mat2By2 m, int n)

Listing 6: A Naive Matrix Exponentiation Method

1 /**

2 * Computes the power of the specified matrix by performing n-1

3 * multiplications when the power is n

4 * @param m a 2x2 matrix of BigInteger objects

5 * @param n a positive integer representing the exponent

6 * @return the power of the specified matrix (m^n)

7 * @throws IllegalArgumentException when n

8 */

9 private static Mat2By2 naivePower(Mat2By2 m, int n)

The main method will perform the following tasks: 1. Create the two 2 2 matrices whose entries are BigInteger objects and display them as shown in the sample run. 2. Using the relevant methods of the Mat2By2 class, compute and display (m1 m2)(m1 + m2), where m1 and m2 are the first and second matrices. Also, compute and display the determinant of (m1 m2)(m1 + m2) using the relevant Mat2By2 methods. 3. Prompt the user for n and using the fastPower method and an accessor method, compute and display the n th Fibonacci number. 4. Next, your program will generate the following terms of the Fibonaccia sequence, 1000, 1500, 2000, 2500 , 10000. For each term, your program will use the fast and naive exponentiation methods. Your program will display the execution times in microseconds that it takes for each method as shown in the table in the sample run below, and I will also have my current state of my program with it. If you can help me make these modifications, then that will be very appreciative.

// First thing I've created when starting a new project on NetBeans IDE 8.2 and named it MatrixExponentiationDemo.java

MatrixEponentiationDemo.java

/* * To change this license header, choose License Headers in Project Properties. * To change this template file, choose Tools | Templates * and open the template in the editor. */ package matrixexponentiationdemo;

/** * * @author */ import java.math.BigInteger;

public class MatrixExponentiationDemo { // this function returns the nth Fibonacci number using the fast power method private static BigInteger fib_fast(Mat2By2 m, int n) { Mat2By2 F = new Mat2By2(BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(0)); if (n == 0) return Mat2By2.valueOf(0); Mat2By2 res = new Mat2By2(F.fastPower(n-1)); return res.me11; } // function that returns the nth Fibonacci number using the naive method private static BigInteger fib_naive(Mat2By2 m, int n) { Mat2By2 F = new Mat2By2(BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(0)); if (n == 0) return BigInteger.valueOf(0); Mat2By2 res = new Mat2By2(F.naivePower(n-1)); return res.me11; } }

// second, I created an interface for the project called Mat2By2API.java

Mat2By2API.java

import java.math.BigInteger;

/* * The interface for a streamlined 2x2 matrix whose * entries are 'Big Integers'. This interface provides the * public instance methods for basic 2x2 matrix operations: * addition, subtraction, multiplication and determinant. * @author Duncan * @since 99/99/9999 */ public interface Mat2By2API { /** * Computes the sum of this matrix and the specified matrix * @param augend holds a 2x2 BigInt matrix * @return the sum of this 2x2 matrix and the specified 2x2 matrix * @throws IllegalArgumentException when augend is not a Mat2By2 object. */ Mat2By2API add(Mat2By2API augend); /** * Computes the difference of this matrix and the specified matrix * @param subtrahend holds a 2x2 BigInt matrix * @return the difference of this 2x2 matrix and the specified 2x2 matrix * @throws IllegalArgumentException when subtrahend is not a Mat2By2 object. */ Mat2By2API subtract(Mat2By2API subtrahend); /** * Computes the product of this matrix and the specified matrix * @param multiplier holds a 2x2 BigInt matrix * @return the product of this 2x2 matrix and the specified 2x2 matrix * @throws IllegalArgumentException when multiplier is not a Mat2By2 object. */ Mat2By2API multiply(Mat2By2API multiplier); /** * Gives the determinant of this matrix * @return the determinant of this matrix */ BigInteger determinant(); /** * Gives the string representation of this matrix in in-line format: * [[top-left, top-right], [bottom-left, bottom-right]] * @return a string representation of this 2x2 matrix in in-line * notation. */ String toString(); /** * Gives the top-left entry of this matrix * @return the top-left entry */ BigInteger getTopLeft(); /** * Gives the top-right entry of this matrix * @return the top-right entry */ BigInteger getTopRight(); /** * Gives the bottom-left entry of this matrix * @return the bottom-left entry */ BigInteger getBottomLeft(); /** * Gives the bottom-right entry of this matrix * @return the bottom-right entry */ BigInteger getBottomRight(); }

// Third and final, I created a class and named it Mat2By2.java

Mat2By2.java

import java.math.BigInteger; import java.util.Scanner;

public class Mat2By2 implements Mat2By2API { // declares the big integers needed for the Matrix Elements (me) for the program BigInteger [] [] entries ; //BigInteger me12; //BigInteger me21; //BigInteger me22; // default constructgor initialized the matrix to identitiy matrix // NOTE: Create public Mat2By2(){ entries [0][0] = BigInteger.valueOf(1); entries [0][1] = BigInteger.valueOf(0); entries [1][0] = BigInteger.valueOf(0); entries [1][1] = BigInteger.valueOf(1); } /** * Creates a 2x2 matrix with the specified entries * @param me11 a BigInteger object representing top-left entry * @param me12 a BigInteger object representing top-right entry * @param me21 a BigInteger object representing bottom-left entry * @param me22 a BigInteger object representing bottom-right entry */ public Mat2By2(BigInteger me11, BigInteger me12, BigInteger me21, BigInteger me22){ entries [0][0] = me11; entries [0][1] = me12; entries [1][0] = me21; entries [1][1] = me22; //this.me12 = me12; //this.me21 = me21; //this.me22 = me22; } // copy constructor with elements same as another given matrix public Mat2By2(Mat2By2 m){ entries [0][0] = m.entries[0][0]; entries [0][1] = m.entries [0][1]; entries [1][0] = m.entries [1][0]; entries [1][1] = m.entries [1][1]; //this.me11 = m.me11; //this.me12 = m.me12; //this.me21 = m.me21; //this.me22 = m.me22; }

// FIX THE FOLLOWING BELOW.

// computes the sum of the matrix public Mat2By2 mat_add(Mat2By2 m2){ Mat2By2 result = new Mat2By2();

// fix these. result.entries [0][0] = entries [0][0].add(m2.entries [0][0]); result.entries [0][1] = entries [0][1].add(m2.entries [0][1]); result.entries [1][0] = entries [1][0].add(m2.entries [1][0]); result.entries [1][1] = entries [1][1].add(m2.entries [1][1]); //result.me11 = m1.me11.add(m2.me11); //result.me12 = m1.me12.add(m2.me12); //result.me21 = m1.me12.add(m2.me21); //result.me22 = m1.me12.add(m2.me22); return result; } // computes the subtraction of the matrix public Mat2By2 mat_sub(Mat2By2 m2){ Mat2By2 result = new Mat2By2(); Mat2By2 m1 = new Mat2By2(this);

// fix these. result.entries [0][0] = m1.entries [0][0].subtract(m2.entries [0][0]); result.entries [0][1] = m1.entries [0][1].subtract(m2.entries [0][1]); result.entries [1][0] = m1.entries [1][0].subtract(m2.entries [1][0]); result.entries [1][1] = m1.entries [1][1].subtract(m2.entries [1][1]); //result.me11 = m1.me11.subtract(m2.me11); //result.me12 = m1.me12.subtract(m2.me12); //result.me21 = m1.me21.subtract(m2.me21); //result.me22 = m1.me22.subtract(m2.me22); return result; } // computes the multiplication of the matrix. public Mat2By2 mat_mult(Mat2By2 m2){ Mat2By2 result = new Mat2By2();

//fix these. result.entries [0][0] = entries [0][0].multiply (m2.entries[0][1].multiply(m2.entries[0][1])); result.entries [0][1] = entries [0][1].multiply (m2.entries[0][1].multiply(m2.entries[1][1])); result.entries [1][0] = entries [1][0].multiply (m2.entries[1][1].multiply(m2.entries[1][0])); result.entries [1][1] = entries [1][1].multiply (m2.entries[1][1].multiply(m2.entries[1][1])); //result.me11 = m1.me11.multiply(m2.me11).add(m1.me12.multiply(m2.me21)); //result.me12 = m1.me11.multiply(m2.me12).add(m1.me12.multiply(m2.me22)); //result.me21 = m1.me21.multiply(m2.me11).add(m1.me22.multiply(m2.me21)); //result.me22 = m1.me21.multiply(m2.me12).add(m1.me22.multiply(m2.me22)); return result; }

/* // this function returns the nth Fibonacci number using the fast power method static BigInteger fib_fast(int n) { Mat2By2 F = new Mat2By2(BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(0)); if (n == 0) return BigInteger.valueOf(0); Mat2By2 res = new Mat2By2(F.fastPower(n-1)); return res.me11; } // function that returns the nth Fibonacci number using the naive method static BigInteger fib_naive(int n) { Mat2By2 F = new Mat2By2(BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(1),BigInteger.valueOf(0)); if (n == 0) return BigInteger.valueOf(0); Mat2By2 res = new Mat2By2(F.naivePower(n-1)); return res.me11; } */

// calculate the matrix determinant public BigInteger determinant(){ BigInteger ans; ans = entries [0][0].multiply(entries[1][1]).subtract(entries[1][0].multiply(entries[0][1])); //ans = this.me11.multiply(this.me22).subtract(this.me21.multiply(this.me12)); return ans; }

// implements methods from the Mat2By2API interface public BigInteger getTopLeft(){ return entries [0][0]; } public BigInteger getTopRight(){ return entries [0][1]; } public BigInteger getBottomLeft(){ return entries [1][0]; } public BigInteger getBottomRight(){ return entries [1][1]; }

// nth of power of the matrix naive method public Mat2By2 naivePower(int n){ Mat2By2 result = new Mat2By2(); Mat2By2 m = new Mat2By2(this); for(int i=0; i result = result.mat_mult(m); } return result; } // nth power of the matrix fast method public Mat2By2 fastPower(int n){ Mat2By2 result = new Mat2By2(); Mat2By2 m = new Mat2By2(this); for(int i=0; i result = result.mat_mult(m); } return result; } // display a matrix as list of list public void display(){ System.out.println("[[" + entries[0][0] + ", " + entries[0][1] + "], [" + entries[1][0] + ", " + entries [1][1] +"]]"); //System.out.println("[[" + this.me11+ ", " + this.me12 + "], [" + this.me21 + ", " + this.me22 + "]]"); }

/** * @param args the command line arguments */ // main method of the program public static void main(String[] args) { Scanner scan = new Scanner(System.in); Mat2By2 m1; Mat2By2 m2; // declares variables for the user to input numbers in the following matrices BigInteger tl,tr, bl, br; //tl(top-left), tr(top-right), bl(bottom-left), br(bottom-right) // prompts user to make input for the first matrix System.out.println("Enter the top-left, top-right bottom-left and bottom-right entries of the first matrix: "); tl = scan.nextBigInteger(); tr = scan.nextBigInteger(); bl = scan.nextBigInteger(); br = scan.nextBigInteger(); m1 = new Mat2By2(tl,tr,bl,br); // prompts user to make input for the second matrix System.out.println(" Enter the top-left, top-right bottom-left and bottom-right entries of the second matrix: "); tl = scan.nextBigInteger(); tr = scan.nextBigInteger(); bl = scan.nextBigInteger(); br = scan.nextBigInteger(); m2 = new Mat2By2(tl,tr,bl,br); // displays matrix m1 System.out.print(" m1 = "); m1.display(); // displays matrix m2 System.out.print("m2 = "); m2.display(); // prints the results of the matrix product System.out.print(" (m1 - m2)(m1 + m2) = "); Mat2By2 m = m1.mat_sub(m2).mat_mult(m1.mat_add(m2)); m.display(); // prints the determinant of the matrix product System.out.print("|(m1 - m2)(m1 + m2)| = " + m.determinant()); System.out.print(" "); // prints the result of matrices based on m1-m2 & m1+m2 created from the user's input // seems to only output number 1 as a result no matter how many numbers I input. // seems to only work with 0 though. System.out.println(" Which Fibonaci number do you wish to compute? "); int n = scan.nextInt(); System.out.println("Fib("+n+") = "+fib_fast(n)); // using fast power method System.out.println("Fib("+n+") = "+fib_naive(n)); // using naive method // outputs the analysis table System.out.println(" Empirical Analysis of naive vs. Fast Matrix Exponentiation in Generating 19 Terms of the Fibonacci Sequence. "); System.out.println("============================================================"); System.out.println("Term\t\tNaive Time(10^-6s)\tFast Time(10^-6s)"); System.out.println("------------------------------------------------------------"); // assigns the integer to 1000 as the start of the empirical analysis instructed in the assignment n = 1000;

long fast_time, naive_time; // lets the empirical analysis run until it reaches 10000. while(n

@Override public Mat2By2API subtract(Mat2By2API subtrahend) { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

@Override public Mat2By2API multiply(Mat2By2API multiplier) { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

@Override public BigInteger getTopLeft() { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

*/

@Override public Mat2By2API add(Mat2By2API augend) { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

@Override public Mat2By2API subtract(Mat2By2API subtrahend) { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

@Override public Mat2By2API multiply(Mat2By2API multiplier) { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. }

/* @Override public BigInteger getTopLeft() { throw new UnsupportedOperationException("Not supported yet."); //To change body of generated methods, choose Tools | Templates. } */

}

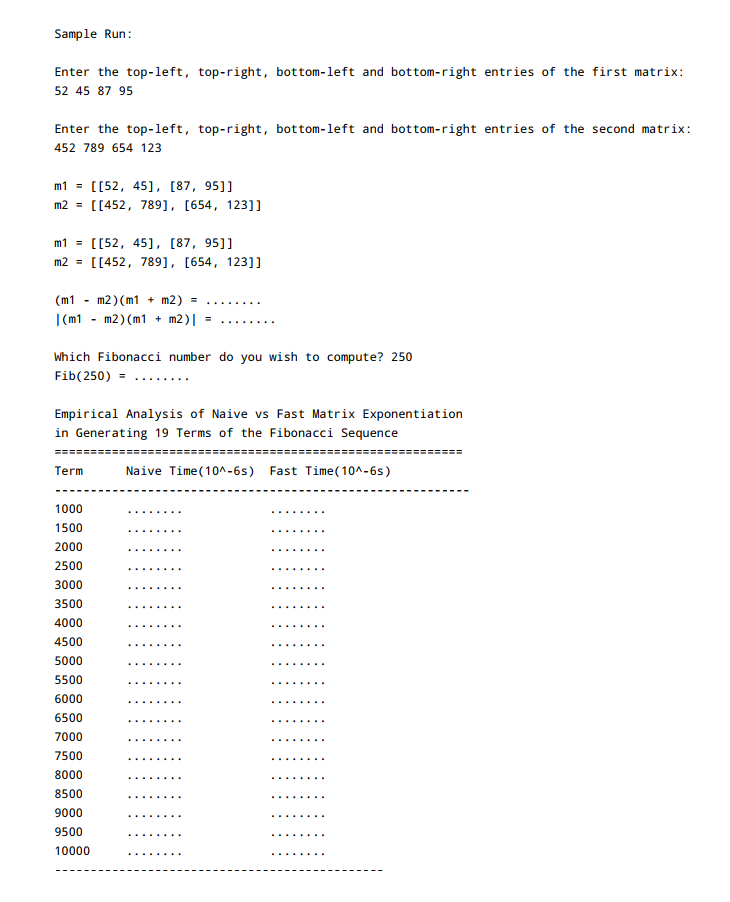
// Now, here is a sample of the program running.

Sample Run Enter the top-left, top-right, bottom-left and bottom-right entries of the first matrix: 52 45 87 95 Enter the top-left, top-right, bottom-left and bottom-right entries of the second matrix: 452 789 654 123 m1[[52, 45], [87, 95]] m2[[452, 789], [654, 123]] m1[[52, 45], [87, 95]] m2[[452, 789], [654, 123]] which Fibonacci number do you wish to compute? 250 Empirical Analysis of Naive vs Fast Matrix Exponentiation in Generating 19 Terms of the Fibonacci Sequence Term Naive Time(10 6s) Fast Time( 10^-6s) 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000 6500 7000 7500 8000 8500 9000 9500 10000