In this problem, a path is any sequence of edges that leads from the root to a leaf of a tree. The length of a
In this problem, a path is any sequence of edges that leads from the root to a leaf of a tree. The length of a path is the number of edges it traverses. So a path from A to B to C to D has length 3.
Here is the pseudocode for standard mergesort:
// Sorts A[lo .. hi] into ascending order mergesort_normal (A, lo, hi) if (hi-lo >= 1) mid = (lo+hi)/2 mergesort(A, lo, mid) mergesort(A, mid+1, hi) merge(A, lo, mid, hi)
Here is an optimized version that performs the merge operation only if the last element of the first half of the array is greater than the first element of the second half of the array:
// Sorts A[lo .. hi] into ascending order mergesort_optimized (A, lo, hi) if (hi-lo >= 1) mid = (lo+hi)/2 mergesort(A, lo, mid) mergesort(A, mid+1, hi) if (A[mid] > A[mid+1] merge(A, lo, mid, hi)
Suppose you draw two decision trees for both mergesorts when applied to an array of 4 elements. What will be the exact length of the longest and shortest paths in the tree for both of these trees?
What is the shortest length of the decision tree for mergesort_optimized when applied to an array size 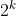 ?
?
Step by Step Solution
There are 3 Steps involved in it
Step: 1

See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


