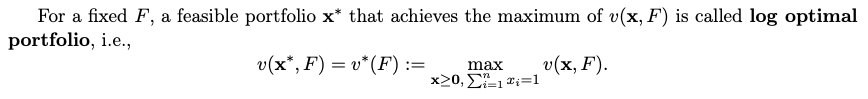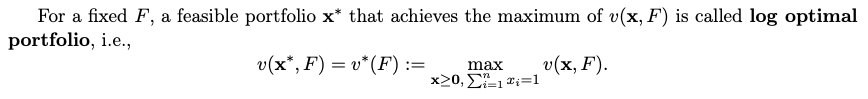
In this section we consider logarithmic utility maximisation problem. As in Markowitz Portfolio Theory, there is a random vector of returns on n stocks R= [R1, R2, ..., Rn. The objective is to maximise the expected logarithmic utility of the final wealth W1, i.e., Elog(W )] = E(log(W x*(1+R))] = E(log(x+(1+R))] + log(Wo) where Wo is initial wealth. To ensure well-posedness of the problem there is no-shortselling constraint imposed on feasible portfolio vector x, that is x = [21, 22, ..., xn) ER" satisfies Ii > O for i = 1, ..., n and 2-1 X; = 1. Let us introduce R:=1+R = (1 + R1,1 + R2, ...,1+Rn), and denote the cumulative distribution function of R by F, i.e., F(y) := P(R 0, Xi = 1 i=1 Note that the above expectation is computed with respect to the distribution of R which is uniquely determined by F. For a fixed F, a feasible portfolio x* that achieves the maximum of v(x, F) is called log optimal portfolio, i.e., v(x*,F) = v*(F):= max v(x, F). x>0, 21;=1 6. (a) Show that (i) v(x,F) is concave in x and linear in F, (ii) v*(F) is convex, (iii) the set of log optimal portfolios with respect to a fixed F is convex. (b) Prove the following theorem: Theorem: The log optimal portfolio x* for a fixed distribution F satisfies the following necessary and sufficient conditions: ES_Ri . [(x*)TR =1 if x; > 0, [ Ri ] F(x*T Si if x = 0. Hint: Using 6(a)(i) argue that log optimal portfolio can be characterised locally by an appropriate condition on the directional derivative of u in the direction from x* to any other feasible portfolio x. In this section we consider logarithmic utility maximisation problem. As in Markowitz Portfolio Theory, there is a random vector of returns on n stocks R= [R1, R2, ..., Rn. The objective is to maximise the expected logarithmic utility of the final wealth W1, i.e., Elog(W )] = E(log(W x*(1+R))] = E(log(x+(1+R))] + log(Wo) where Wo is initial wealth. To ensure well-posedness of the problem there is no-shortselling constraint imposed on feasible portfolio vector x, that is x = [21, 22, ..., xn) ER" satisfies Ii > O for i = 1, ..., n and 2-1 X; = 1. Let us introduce R:=1+R = (1 + R1,1 + R2, ...,1+Rn), and denote the cumulative distribution function of R by F, i.e., F(y) := P(R 0, Xi = 1 i=1 Note that the above expectation is computed with respect to the distribution of R which is uniquely determined by F. For a fixed F, a feasible portfolio x* that achieves the maximum of v(x, F) is called log optimal portfolio, i.e., v(x*,F) = v*(F):= max v(x, F). x>0, 21;=1 6. (a) Show that (i) v(x,F) is concave in x and linear in F, (ii) v*(F) is convex, (iii) the set of log optimal portfolios with respect to a fixed F is convex. (b) Prove the following theorem: Theorem: The log optimal portfolio x* for a fixed distribution F satisfies the following necessary and sufficient conditions: ES_Ri . [(x*)TR =1 if x; > 0, [ Ri ] F(x*T Si if x = 0. Hint: Using 6(a)(i) argue that log optimal portfolio can be characterised locally by an appropriate condition on the directional derivative of u in the direction from x* to any other feasible portfolio x