Question: . Instructions: Download a version of this document . Update the document with the required information Save the document Upload the document as your submission
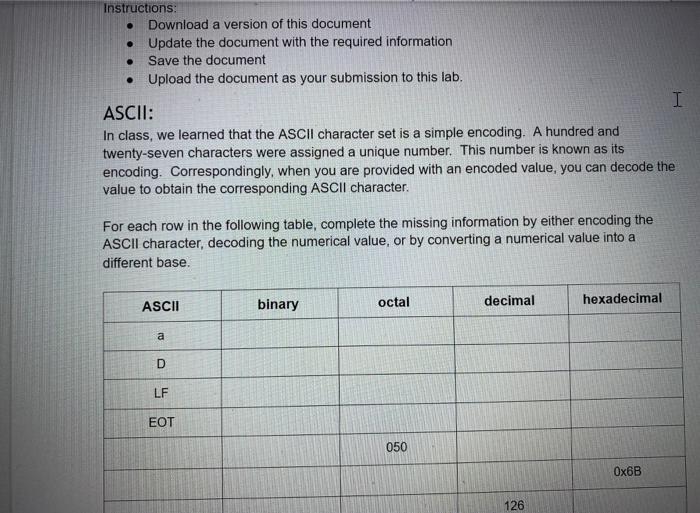
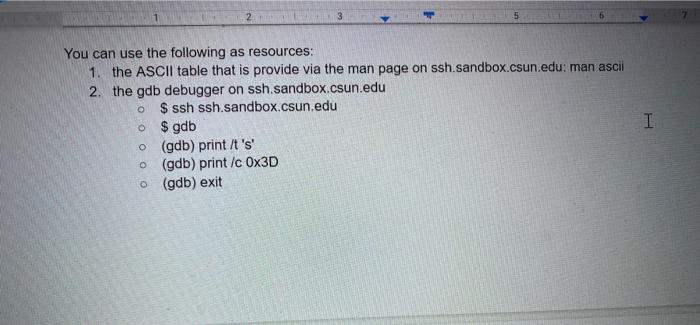
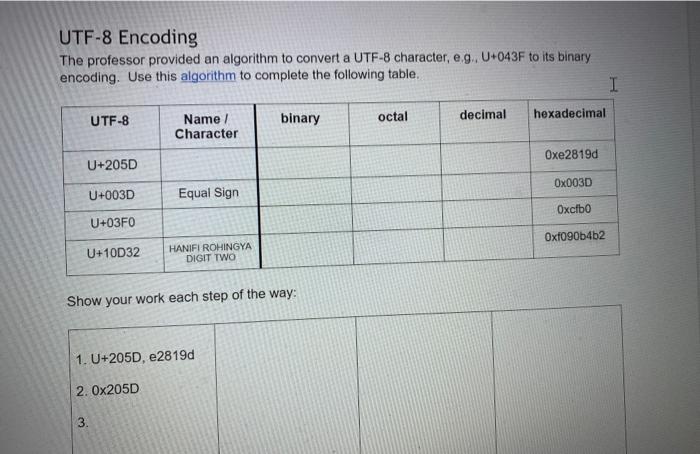
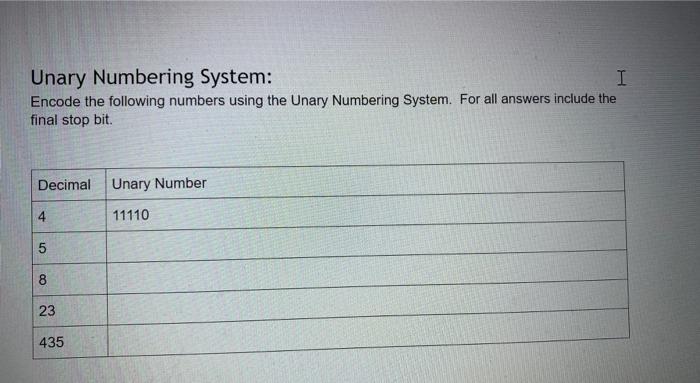
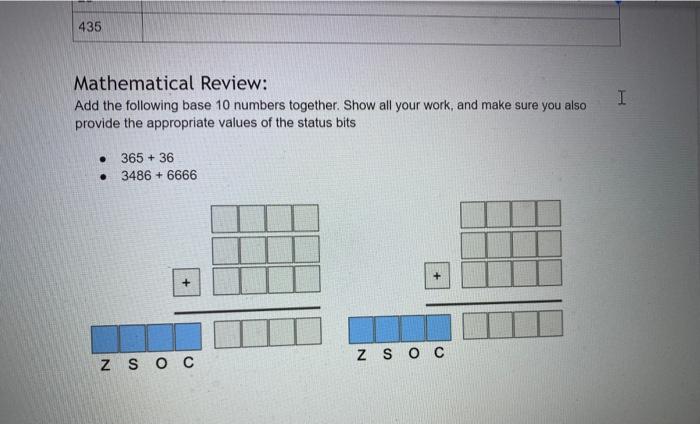
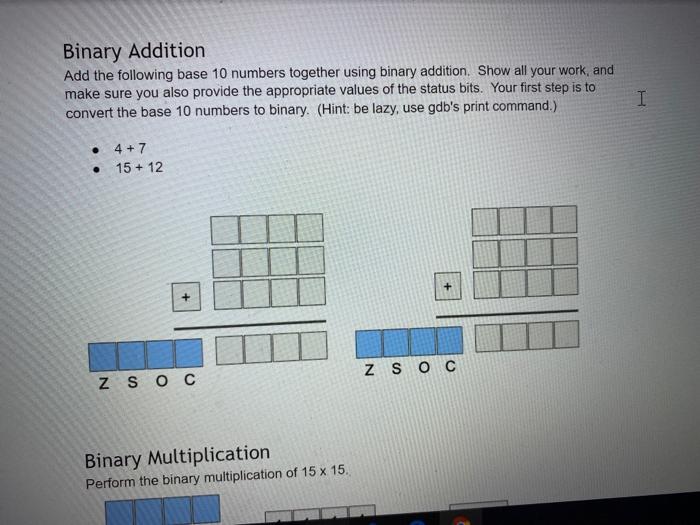
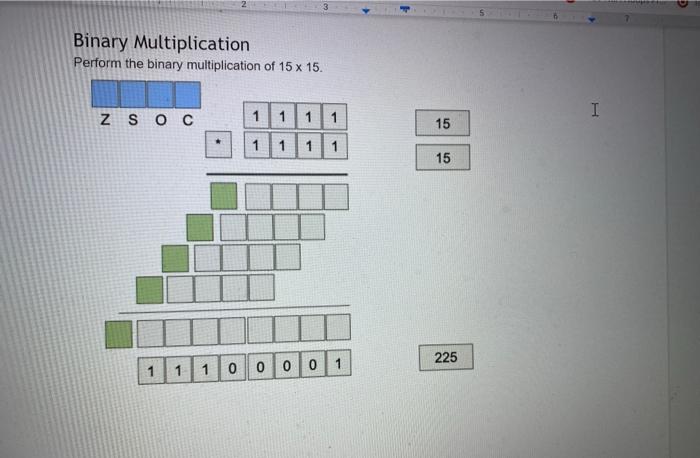
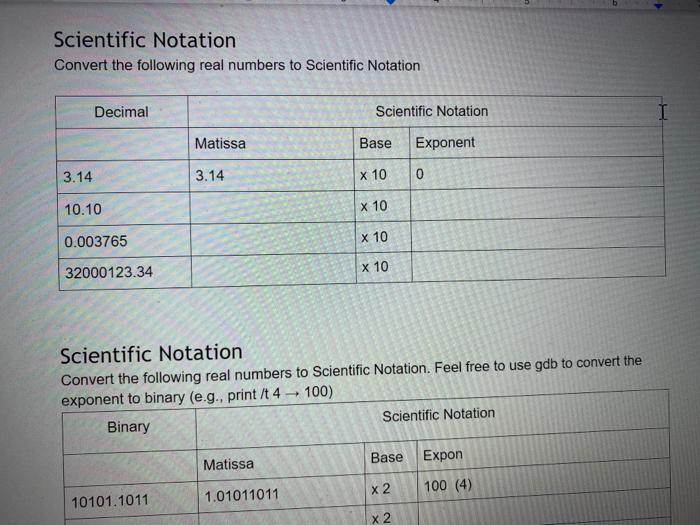
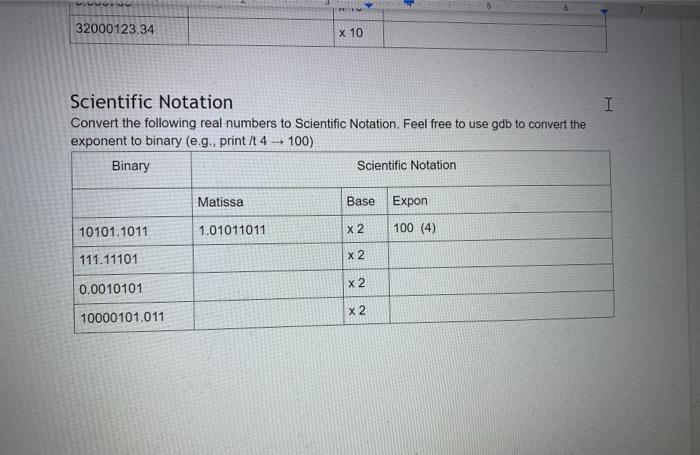
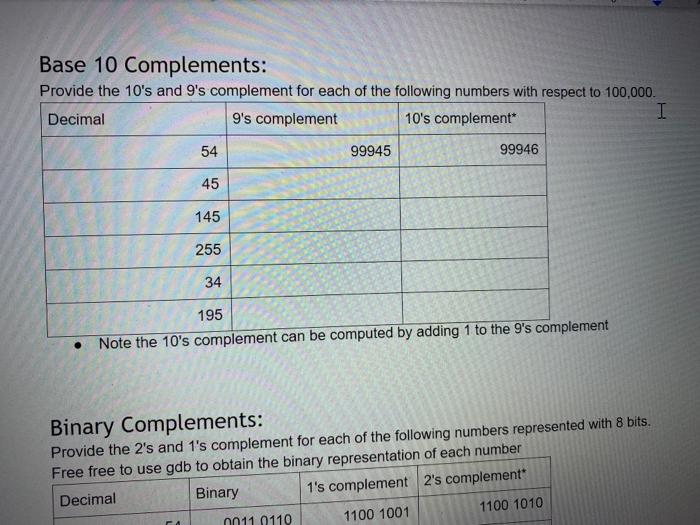
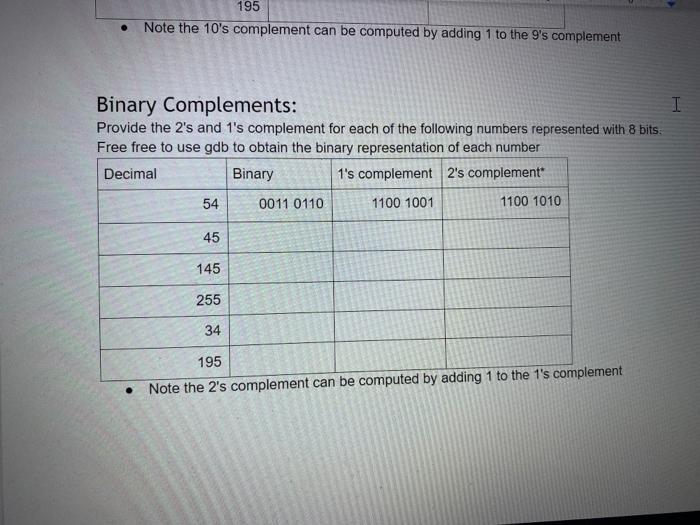
. Instructions: Download a version of this document . Update the document with the required information Save the document Upload the document as your submission to this lab. . ASCII: I In class, we learned that the ASCII character set is a simple encoding. A hundred and twenty-seven characters were assigned a unique number. This number is known as its encoding. Correspondingly, when you are provided with an encoded value, you can decode the value to obtain the corresponding ASCII character. For each row in the following table, complete the missing information by either encoding the ASCII character, decoding the numerical value, or by converting a numerical value into a different base. ASCII binary octal decimal hexadecimal a D LF EOT 050 Ox6B 126 3 O You can use the following as resources: 1. the ASCII table that is provide via the man page on ssh.sandbox.csun.edu: man ascii 2. the gdb debugger on ssh.sandbox.csun.edu $ ssh ssh.sandbox.csun.edu o $ gdb o (gdb) print it's (gdb) print /c 0x3D (gdb) exit I O O UTF-8 Encoding The professor provided an algorithm to convert a UTF-8 character, eg. U+043F to its binary encoding. Use this algorithm to complete the following table. I UTF-8 hexadecimal binary octal decimal Name / Character Oxe2819d U+205D Ox003D U+003D Equal Sign Oxcibo U+03F0 Oxfo90b4b2 U+10D32 HANIFI ROHINGYA DIGIT TWO Show your work each step of the way 1. U+205D, e2819d 2. Ox205D 3. Unary Numbering System: I Encode the following numbers using the Unary Numbering System. For all answers include the final stop bit. Decimal Unary Number 4 11110 5 8 23 435 435 Mathematical Review: Add the following base 10 numbers together. Show all your work, and make sure you also provide the appropriate values of the status bits I 365 + 36 . 3486 + 6666 Z SOC Z SOC Binary Addition Add the following base 10 numbers together using binary addition. Show all your work, and make sure you also provide the appropriate values of the status bits. Your first step is to convert the base 10 numbers to binary. (Hint: be lazy, use gdb's print command.) I 4 +7 15 + 12 Z SO C Z SOC Binary Multiplication Perform the binary multiplication of 15 x 15. Binary Multiplication Perform the binary multiplication of 15 x 15. Z SOC 11 1 I 1 15 11 1 1 15 225 1 1 0 0001 Scientific Notation Convert the following real numbers to Scientific Notation Decimal Scientific Notation Matissa Base Exponent 3.14 3.14 x 10 0 10.10 x 10 0.003765 X 10 32000123.34 x 10 Scientific Notation Convert the following real numbers to Scientific Notation. Feel free to use gdb to convert the exponent to binary (e.g., print/t 4 100) Binary Scientific Notation Matissa Base Expon 100 (4) X2 10101.1011 1.01011011 X2 32000123.34 X 10 I Scientific Notation Convert the following real numbers to Scientific Notation. Feel free to use gdb to convert the exponent to binary (e.g., print/t 4 100) Binary Scientific Notation Matissa Base Expon 10101.1011 1.01011011 X2 100 (4) 111.11101 X2 X2 0.0010101 x2 10000101.011 Base 10 Complements: Provide the 10's and 9's complement for each of the following numbers with respect to 100,000 I Decimal 9's complement 10's complement 54 99945 99946 45 145 255 34 195 Note the 10's complement can be computed by adding 1 to the 9's complement Binary Complements: Provide the 2's and 1's complement for each of the following numbers represented with 8 bits. Free free to use gdb to obtain the binary representation of each number Decimal Binary 1's complement 2's complement 0011 0110 1100 1001 1100 1010 195 Note the 10's complement can be computed by adding 1 to the 9's complement I Binary Complements: Provide the 2's and 1's complement for each of the following numbers represented with 8 bits Free free to use gdb to obtain the binary representation of each number Decimal Binary 1's complement 2's complement 54 0011 0110 1100 1001 1100 1010 45 145 255 34 195 Note the 2's complement can be computed by adding 1 to the 1's complement
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


