Isaac Newton's method to approximate square roots works like this: given an approximation x of 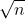, a better approximation is 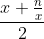, Repeat until you get the desired precision. Write a subroutine sqrt implementing Newton's algorithm for approximating a square root. Start with an arbitrary guess for the approximation (1.0 is a good starting point), and loop until your approximation squared is within of n, i.e. 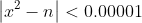. (A better way is to test if the absolute value of the ratio, , is close to zero - why?) You may adapt the given newton.s program for this. Write a MIPS program that prompts the user for the (x, y) coordinates of two points in the real (Cartesian) plane, and then calculates and displays the distance between the points with reasonable descriptive text. Prompt for the coordinates using a little subroutine using simple linkage do not duplicate the code for this. Calculate the distance by using the Pythagorean Theorem: 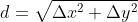Use all single-precision (32-bit float) arithmetic for this assignment. Use the simple register-based linkage convention (arguments in $a registers, return value in $v0, nothing on the stack) for this program.

Here is the code for the newton.s program:

## newton.s -- compute sqrt(n) ## given an approximation x to sqrt(n), ## an improved approximation is: ## x' = (1/2)(x + n/x) ## Register use: ## $f0 --- n ## $f1 --- 1.0 ## $f2 --- 2.0 ## $f3 --- x : current approx. ## $f4 --- x' : next approx. ## $f8 --- temp .text .globl __start __start: li $v0, 4 # print string la $a0, prompt # address of prompt string syscall # print the prompt li $v0, 5 # read integer syscall # get the integer mtc1 $v0, $f0 # move integer to coprocessor 1 cvt.s.w $f1, $f0 # convert entered integer to single s.s $f1, n # store it in n nop # store delay slot # start Newton's algorithm to approximate square root l.s $f0, n # get n li.s $f1, 1.0 # constant 1.0 li.s $f2, 2.0 # constant 2.0 li.s $f3, 1.0 # x == first approx. li.s $f10, 1.0e-5 # five figure accuracy loop: mov.s $f4, $f0 # x' = n div.s $f4, $f4,$f3 # x' = n/x add.s $f4, $f3,$f4 # x' = x + n/x div.s $f3, $f4,$f2 # x = (1/2)(x + n/x) mul.s $f8, $f3, $f3 # check: x^2 div.s $f8, $f0, $f8 # n/x^2 sub.s $f8, $f8, $f1 # n/x^2 - 1.0 abs.s $f8, $f8 # |n/x^2 - 1.0| c.lt.s $f8, $f10 # |x^2 - n|