 Java
Java
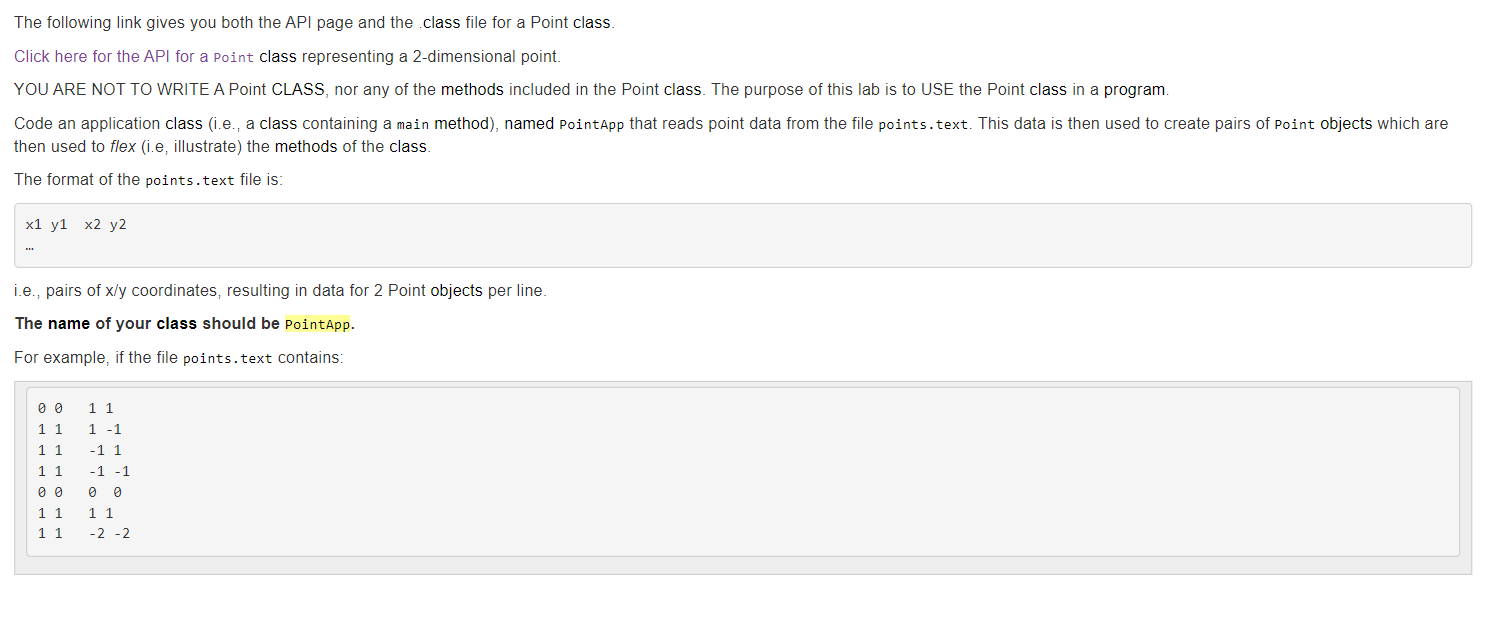
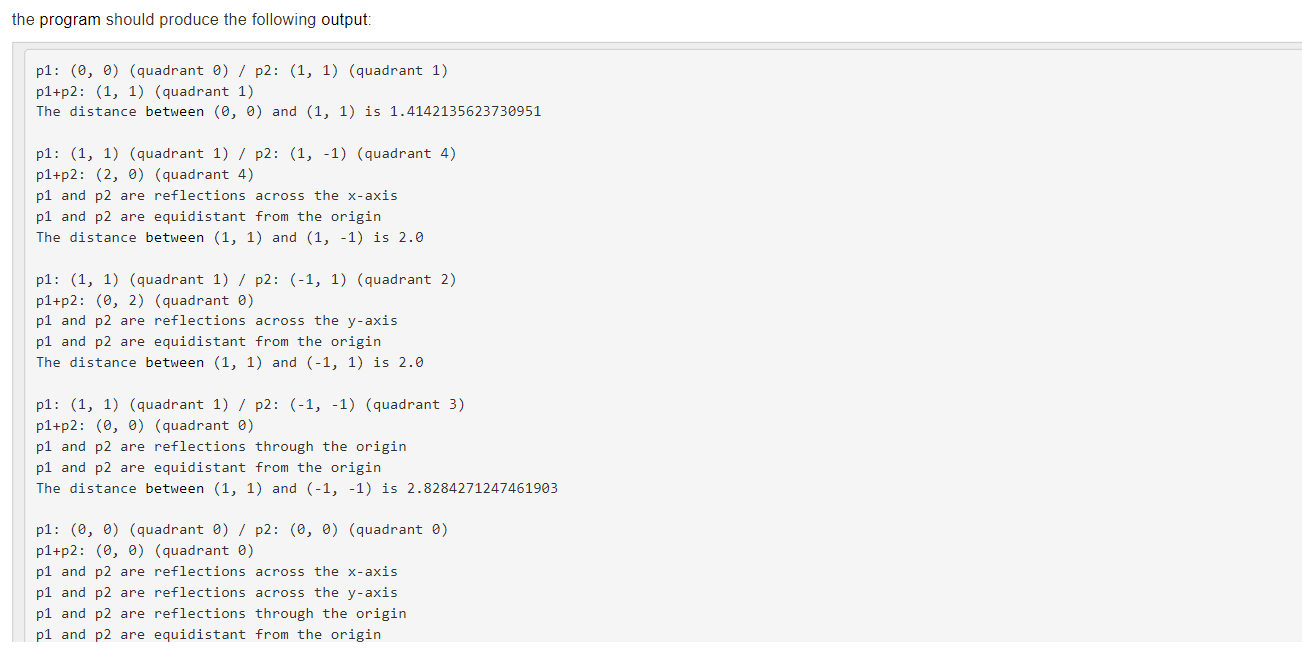
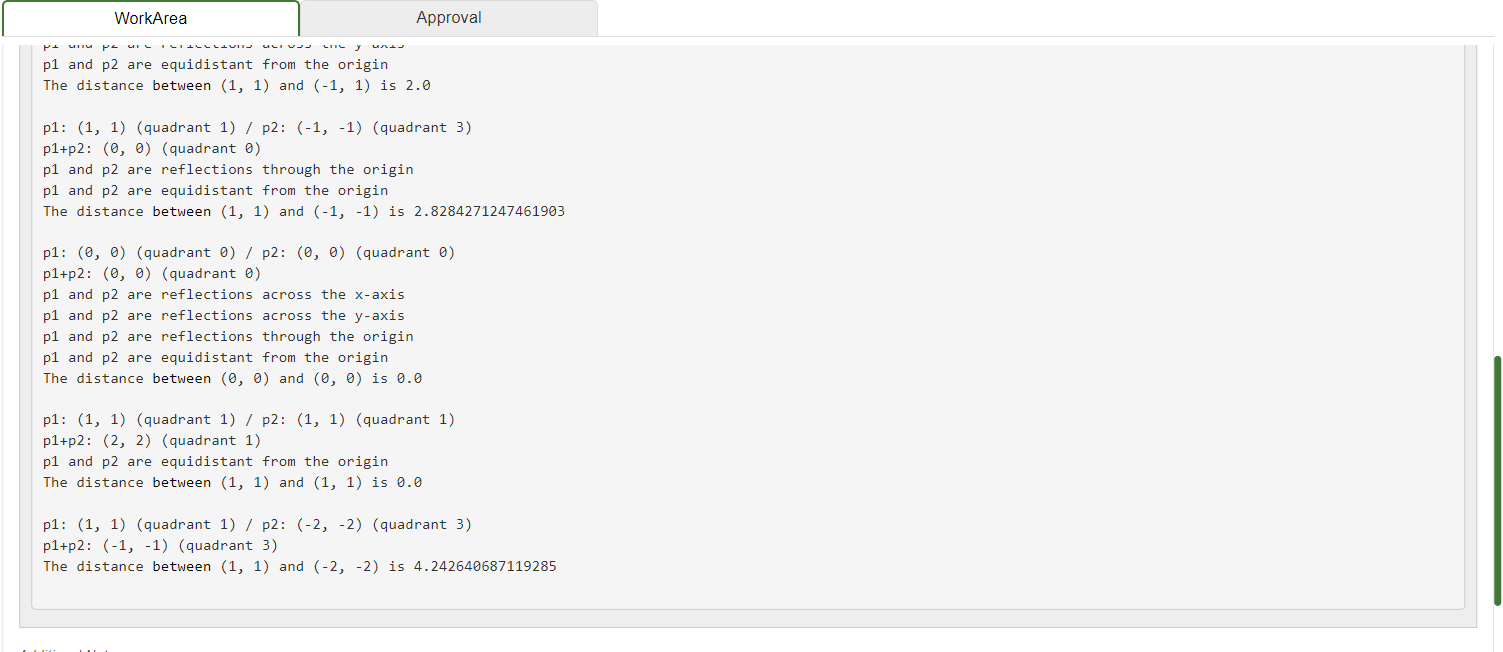
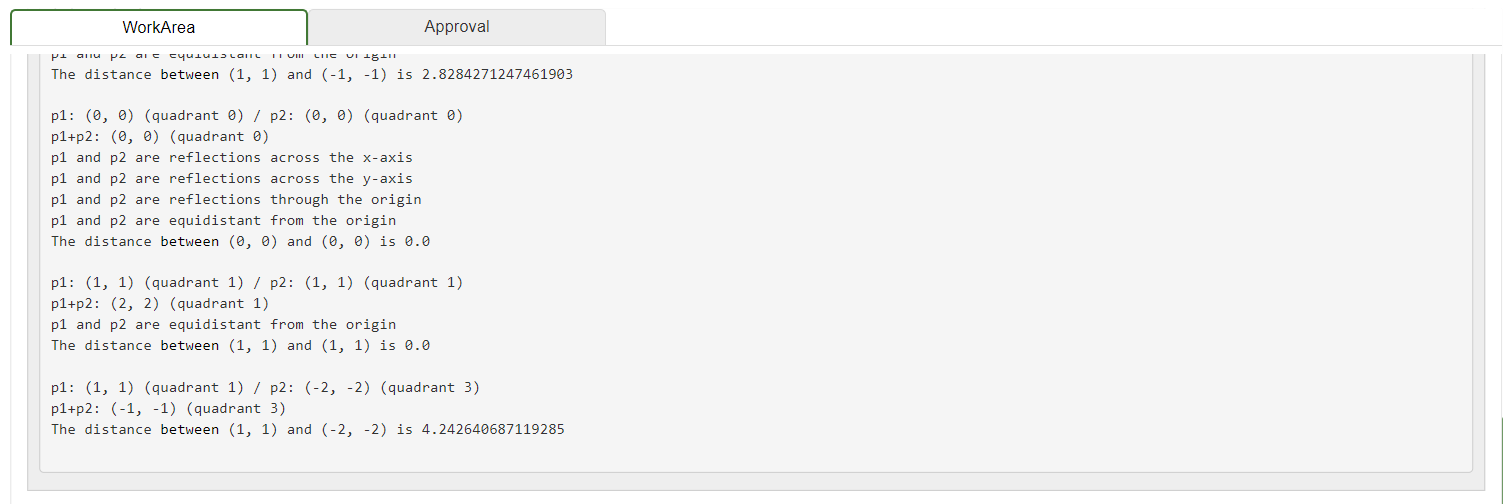
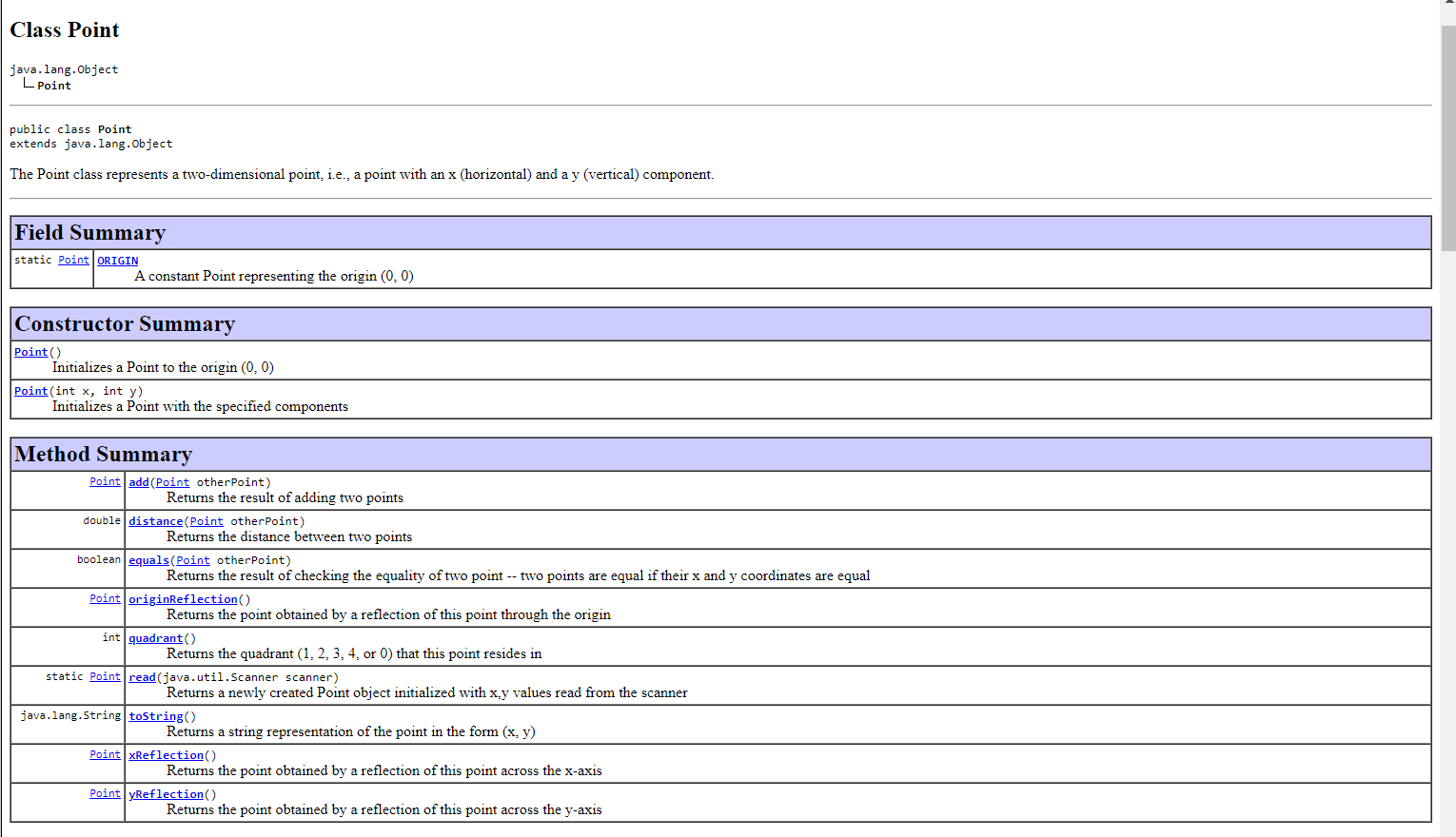
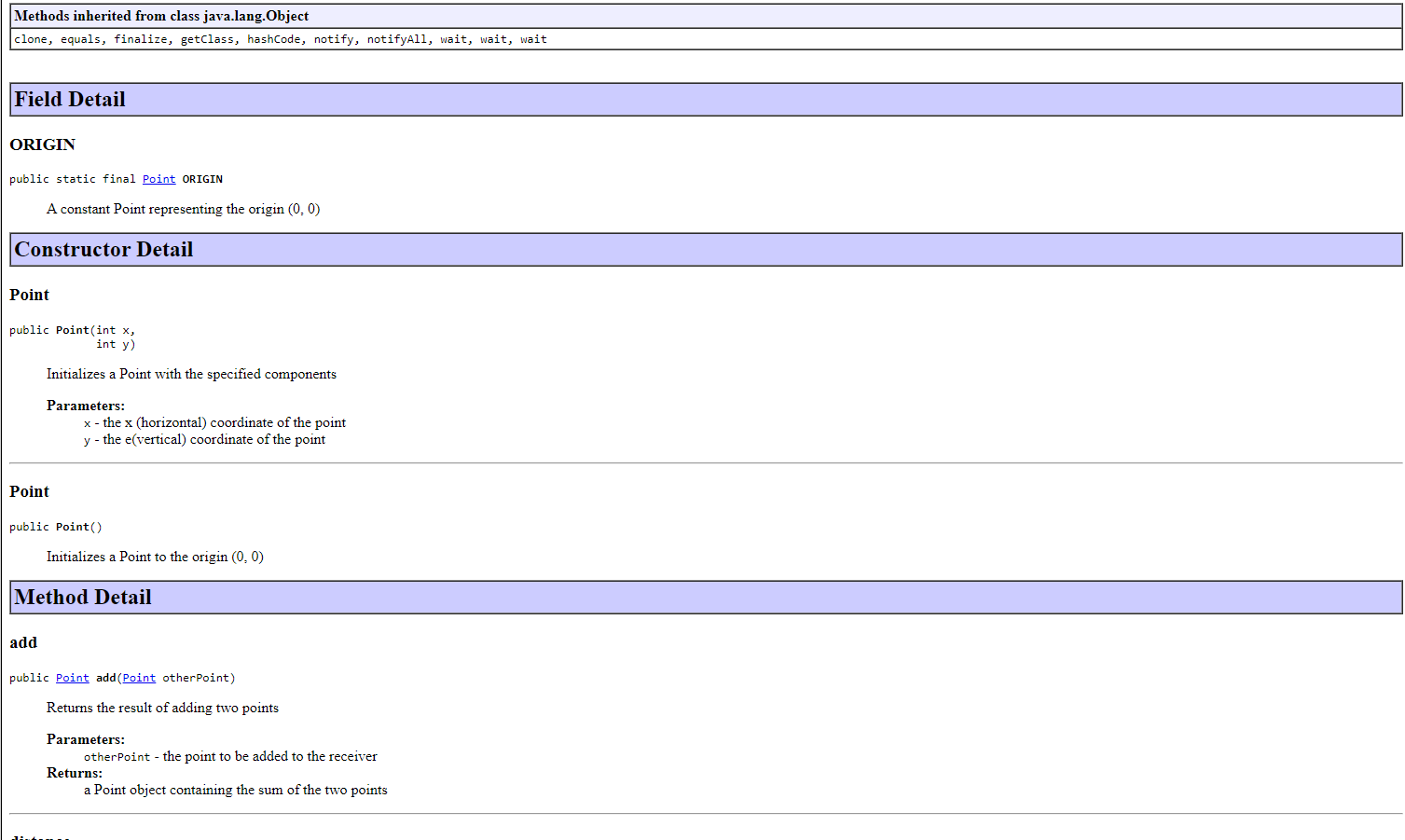
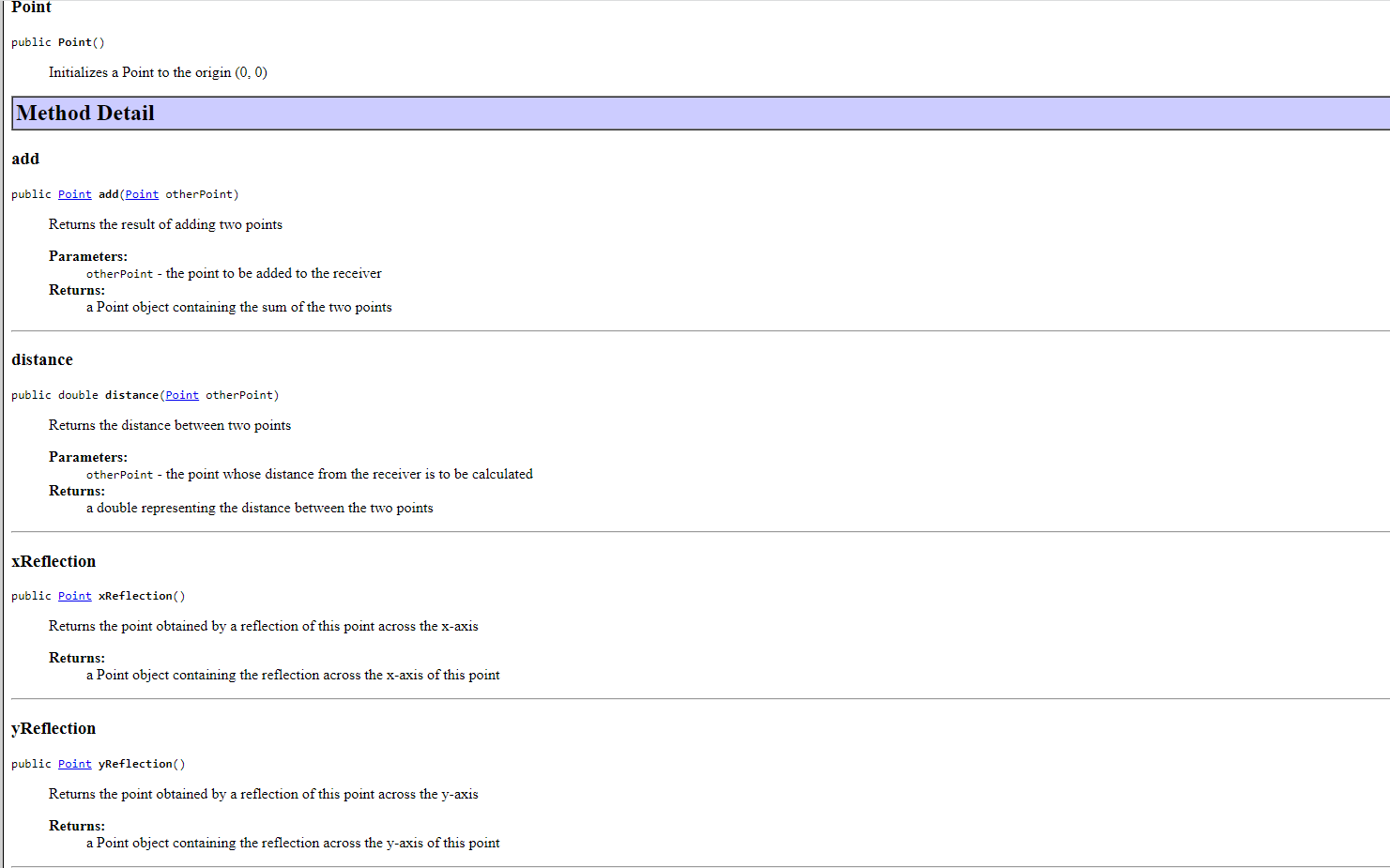
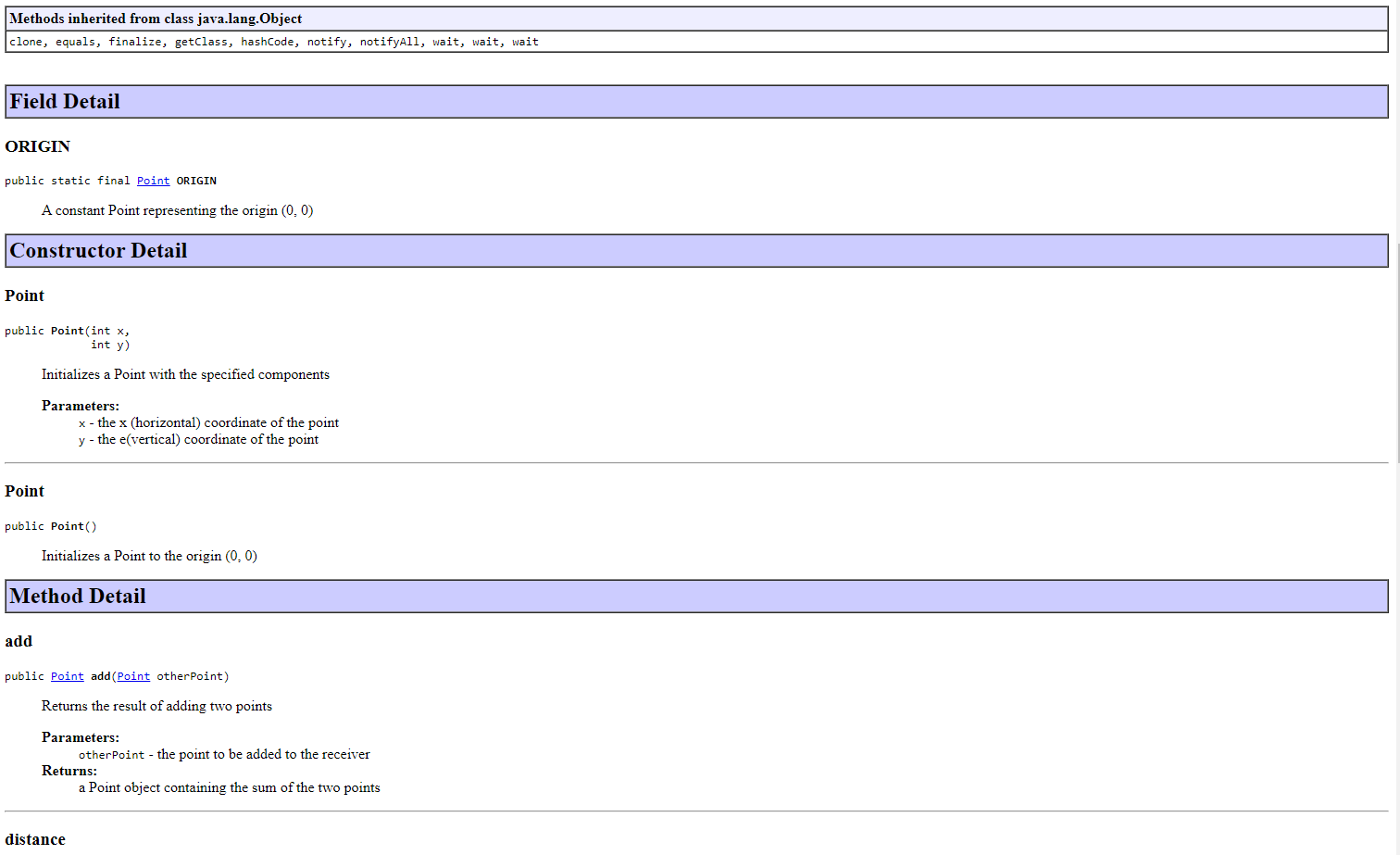
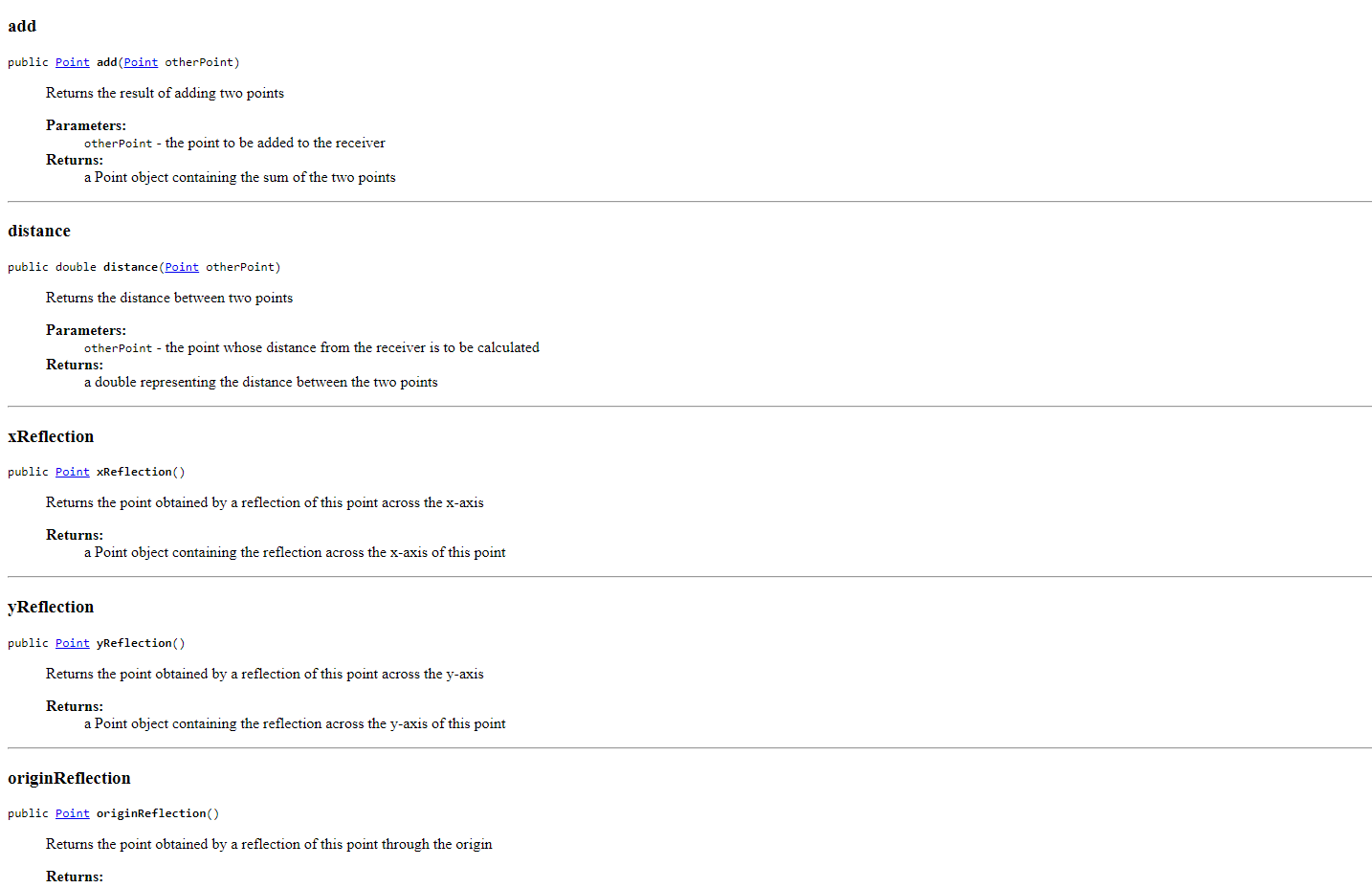
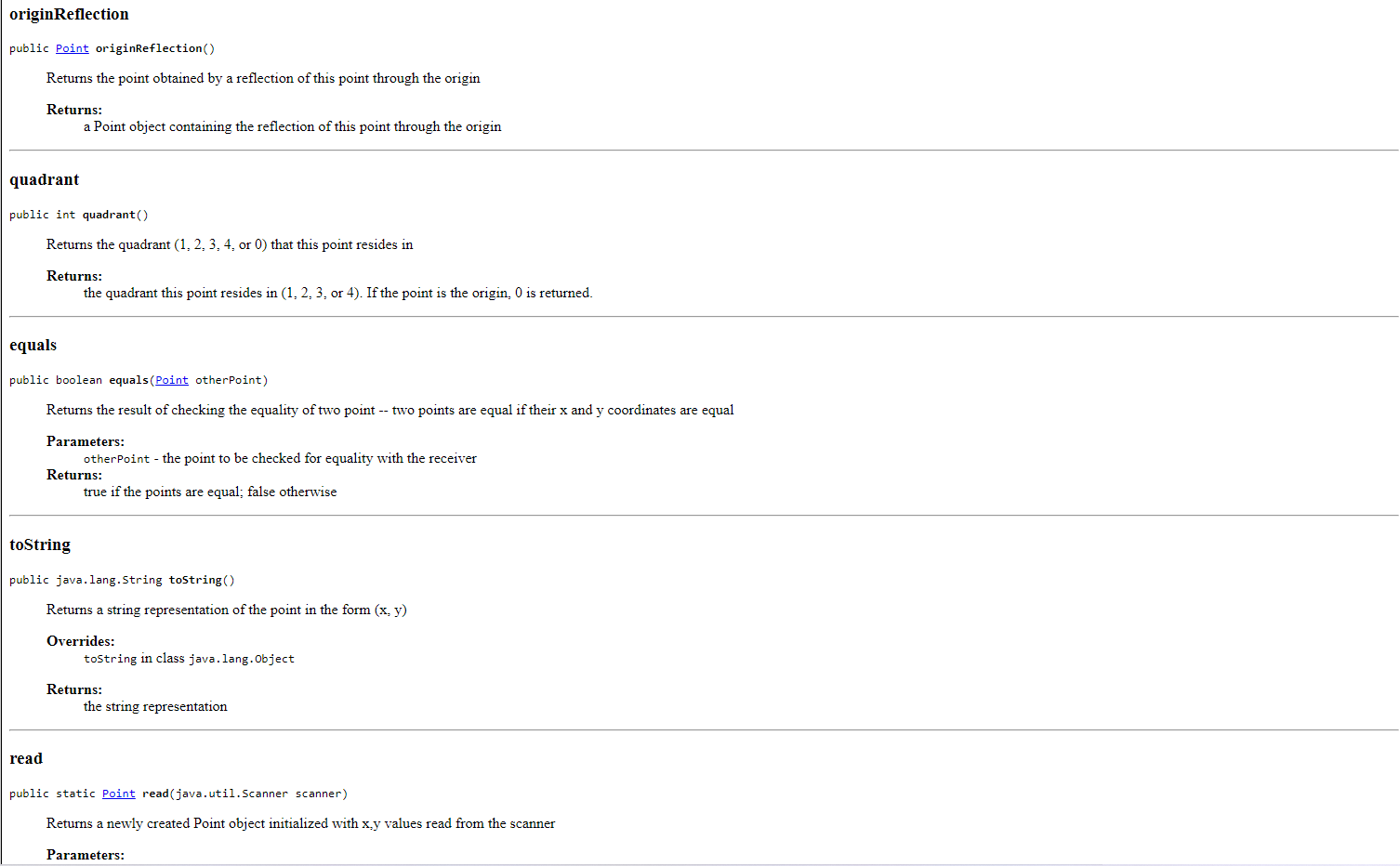
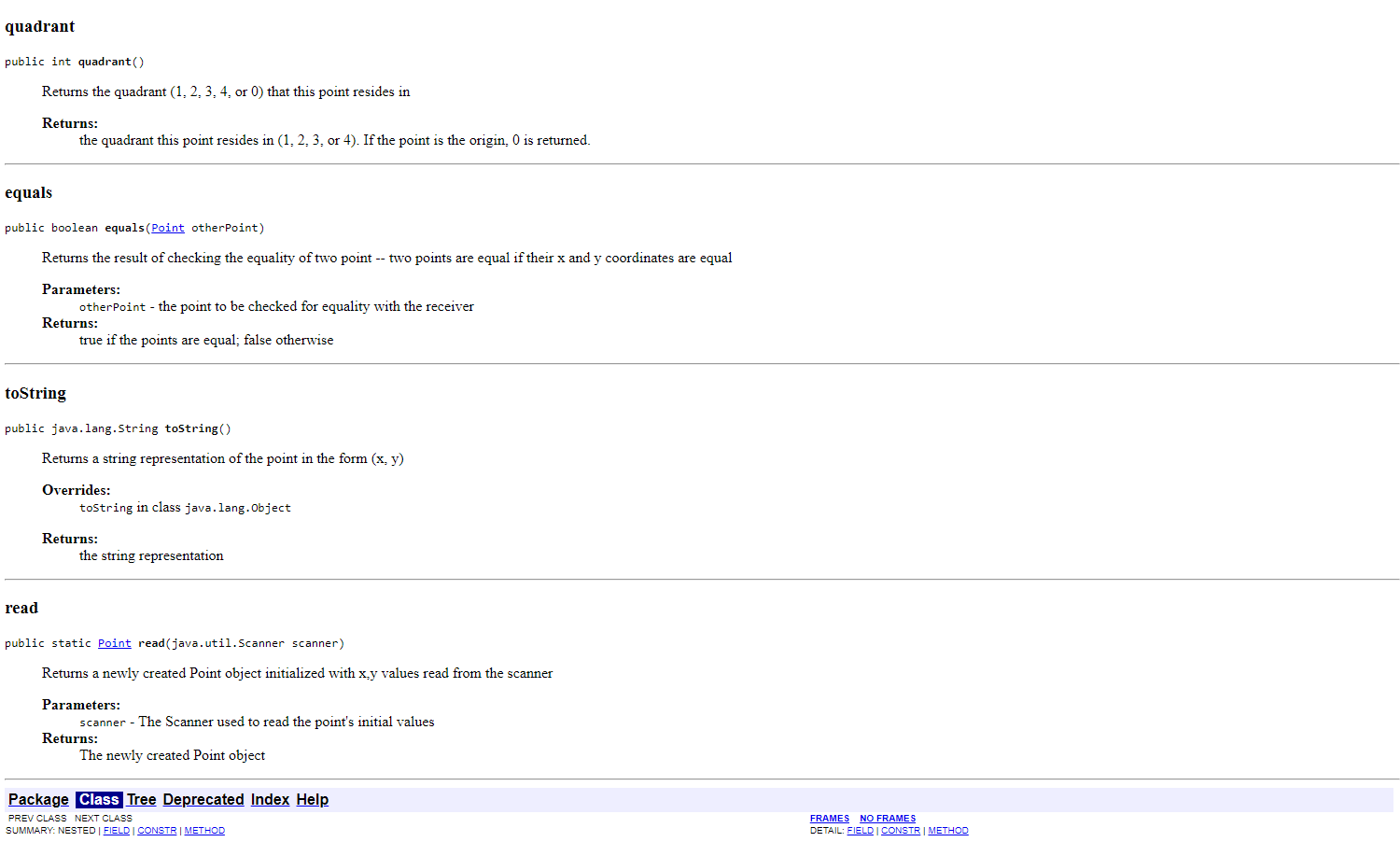
The following link gives you both the API page and the .class file for a Point class. Click here for the API for a Point class representing a 2-dimensional point. YOU ARE NOT TO WRITE A Point CLASS, nor any of the methods included in the Point class. The purpose of this lab is to USE the Point class in a program. then used to flex (i.e, illustrate) the methods of the class. The format of the points.text file is: x1 y 1 x y 2 i.e., pairs of x/y coordinates, resulting in data for 2 Point objects per line. The name of your class should be PointApp. For example, if the file points.text contains: 001111111111111111111122 the program should produce the following output: p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 2.0 p1: (1, 1) (quadrant 1) / p2: (1,1) (quadrant 3) p1+p2:(0,0) (quadrant ) p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 2.8284271247461903 p1:(0,0) (quadrant )/p2:(,0) (quadrant ) p1+p2:(0,0) (quadrant 0 ) p1 and p2 are reflections across the x-axis p1 and p2 are reflections across the y-axis p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (,) and (,) is . p1: (1, 1) (quadrant 1) / p2: (1, 1) (quadrant 1) p1+p2: (2,2) (quadrant 1) p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 0.0 p1: (1, 1) (quadrant 1) / p2: (2,2) (quadrant 3) p1+p2:(1,1) (quadrant 3) The distance between (1,1) and (2,2) is 4.242640687119285 The distance between (1,1) and (1,1) is 2.8284271247461903 p1: (0,0) (quadrant 0)/p2:(0,0) (quadrant 0) p1+p2: (0,0) (quadrant 0) p1 and p2 are reflections across the x-axis p1 and p2 are reflections across the y-axis p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (0, 0) and (0,0) is 0.0 p1: (1, 1) (quadrant 1)/p2:(1,1) (quadrant 1) p1+p2: (2, 2) (quadrant 1) p1 and p2 are equidistant from the origin The distance between (1, 1) and (1, 1) is 0.0 p1: (1, 1) (quadrant 1)/p2:(2,2) (quadrant 3) p1+p2: (-1, -1) (quadrant 3 ) The distance between (1, 1) and (-2, -2) is 4.242640687119285 In this exercise, you will be working with a class that represents two-dimensional points (i.e., points with x and y coordinates). (Before you get too nervous... there is no math to be done here :).) referencing. Files and Information Provided to You - Here is the API for the Point class representing a 2-dimensional point. - Here is the .class file for the Point class. You should download it for use while developing the code in your IDE. What You Are to Do flex (i.e., illustrate) the methods of the class. The format of the points.text file is: i.e., pairs of x/y coordinates, resulting in data for 2 Point objects per line. Sample Test Run For example if the file points.text contains: public class Point extends java. lang.Object clone, equals, finalize, getClass, hashCode, notify, notifyAll, wait, wait, wait Field Detail ORIGIN public static final Point ORIGIN A constant Point representing the origin (0,0) Constructor Detail Point public Point(int x int y ) Initializes a Point with the specified components Parameters: x - the x (horizontal) coordinate of the point y - the e(vertical) coordinate of the point Point public Point() Initializes a Point to the origin (0,0) Method Detail add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points distance public double distance(Point otherPoint) Returns the distance between two points Parameters: otherPoint - the point whose distance from the receiver is to be calculated Returns: a double representing the distance between the two points xReflection public Point xReflection() Returns the point obtained by a reflection of this point across the x-axis Returns: a Point object containing the reflection across the x-axis of this point yReflection public Point yReflection() Returns the point obtained by a reflection of this point across the y-axis Returns: a Point object containing the reflection across the y-axis of this point Methods inherited from class java.lang.Object clone, equals, finalize, getClass, hashCode, notify, notifyAll, wait, wait, wait Field Detail ORIGIN public static final Point ORIGIN A constant Point representing the origin (0,0) Constructor Detail Point public Point(int x int y ) Initializes a Point with the specified components Parameters: x - the x (horizontal) coordinate of the point y - the e(vertical) coordinate of the point Point public Point() Initializes a Point to the origin (0,0) Method Detail add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points distance public double distance(Point otherPoint) Returns the distance between two points Parameters: otherPoint - the point whose distance from the receiver is to be calculated Returns: a double representing the distance between the two points xReflection public Point xReflection() Returns the point obtained by a reflection of this point across the x-axis Returns: a Point object containing the reflection across the x-axis of this point yReflection public Point yReflection() Returns the point obtained by a reflection of this point across the y-axis Returns: a Point object containing the reflection across the y-axis of this point originReflection public point originReflection() Returns the point obtained by a reflection of this point through the origin Returns: a Point object containing the reflection of this point through the origin quadrant public int quadrant () Returns the quadrant (1,2,3,4, or 0) that this point resides in Returns: the quadrant this point resides in (1,2,3, or 4). If the point is the origin, 0 is returned. equals public boolean equals (Point otherPoint) Returns the result of checking the equality of two point -- two points are equal if their x and y coordinates are equal Parameters: otherpoint - the point to be checked for equality with the receiver Returns: true if the points are equal; false otherwise toString public java.lang.String tostring() Returns a string representation of the point in the form (x,y) Overrides: tostring in class java. lang. object Returns: the string representation read public static Point read(java.util.Scanner scanner) Returns a newly created Point object initialized with x,y values read from the scanner Parameters: quadrant public int quadrant() Returns the quadrant (1,2,3,4, or 0) that this point resides in Returns: the quadrant this point resides in (1,2,3, or 4). If the point is the origin, 0 is returned. equals public boolean equals(Point otherPoint) Returns the result of checking the equality of two point -- two points are equal if their x and y coordinates are equal Parameters: otherPoint - the point to be checked for equality with the receiver Returns: true if the points are equal; false otherwise tostring public java.lang. String tostring() Returns a string representation of the point in the form (x, y ) Overrides: tostring in class java. lang. Object Returns: the string representation read public static point read(java.util.Scanner scanner) Returns a newly created Point object initialized with x,y values read from the scanner Parameters: scanner - The Scanner used to read the point's initial values Returns: The newly created Point object The following link gives you both the API page and the .class file for a Point class. Click here for the API for a Point class representing a 2-dimensional point. YOU ARE NOT TO WRITE A Point CLASS, nor any of the methods included in the Point class. The purpose of this lab is to USE the Point class in a program. then used to flex (i.e, illustrate) the methods of the class. The format of the points.text file is: x1 y 1 x y 2 i.e., pairs of x/y coordinates, resulting in data for 2 Point objects per line. The name of your class should be PointApp. For example, if the file points.text contains: 001111111111111111111122 the program should produce the following output: p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 2.0 p1: (1, 1) (quadrant 1) / p2: (1,1) (quadrant 3) p1+p2:(0,0) (quadrant ) p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 2.8284271247461903 p1:(0,0) (quadrant )/p2:(,0) (quadrant ) p1+p2:(0,0) (quadrant 0 ) p1 and p2 are reflections across the x-axis p1 and p2 are reflections across the y-axis p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (,) and (,) is . p1: (1, 1) (quadrant 1) / p2: (1, 1) (quadrant 1) p1+p2: (2,2) (quadrant 1) p1 and p2 are equidistant from the origin The distance between (1,1) and (1,1) is 0.0 p1: (1, 1) (quadrant 1) / p2: (2,2) (quadrant 3) p1+p2:(1,1) (quadrant 3) The distance between (1,1) and (2,2) is 4.242640687119285 The distance between (1,1) and (1,1) is 2.8284271247461903 p1: (0,0) (quadrant 0)/p2:(0,0) (quadrant 0) p1+p2: (0,0) (quadrant 0) p1 and p2 are reflections across the x-axis p1 and p2 are reflections across the y-axis p1 and p2 are reflections through the origin p1 and p2 are equidistant from the origin The distance between (0, 0) and (0,0) is 0.0 p1: (1, 1) (quadrant 1)/p2:(1,1) (quadrant 1) p1+p2: (2, 2) (quadrant 1) p1 and p2 are equidistant from the origin The distance between (1, 1) and (1, 1) is 0.0 p1: (1, 1) (quadrant 1)/p2:(2,2) (quadrant 3) p1+p2: (-1, -1) (quadrant 3 ) The distance between (1, 1) and (-2, -2) is 4.242640687119285 In this exercise, you will be working with a class that represents two-dimensional points (i.e., points with x and y coordinates). (Before you get too nervous... there is no math to be done here :).) referencing. Files and Information Provided to You - Here is the API for the Point class representing a 2-dimensional point. - Here is the .class file for the Point class. You should download it for use while developing the code in your IDE. What You Are to Do flex (i.e., illustrate) the methods of the class. The format of the points.text file is: i.e., pairs of x/y coordinates, resulting in data for 2 Point objects per line. Sample Test Run For example if the file points.text contains: public class Point extends java. lang.Object clone, equals, finalize, getClass, hashCode, notify, notifyAll, wait, wait, wait Field Detail ORIGIN public static final Point ORIGIN A constant Point representing the origin (0,0) Constructor Detail Point public Point(int x int y ) Initializes a Point with the specified components Parameters: x - the x (horizontal) coordinate of the point y - the e(vertical) coordinate of the point Point public Point() Initializes a Point to the origin (0,0) Method Detail add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points distance public double distance(Point otherPoint) Returns the distance between two points Parameters: otherPoint - the point whose distance from the receiver is to be calculated Returns: a double representing the distance between the two points xReflection public Point xReflection() Returns the point obtained by a reflection of this point across the x-axis Returns: a Point object containing the reflection across the x-axis of this point yReflection public Point yReflection() Returns the point obtained by a reflection of this point across the y-axis Returns: a Point object containing the reflection across the y-axis of this point Methods inherited from class java.lang.Object clone, equals, finalize, getClass, hashCode, notify, notifyAll, wait, wait, wait Field Detail ORIGIN public static final Point ORIGIN A constant Point representing the origin (0,0) Constructor Detail Point public Point(int x int y ) Initializes a Point with the specified components Parameters: x - the x (horizontal) coordinate of the point y - the e(vertical) coordinate of the point Point public Point() Initializes a Point to the origin (0,0) Method Detail add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points add public Point add(Point otherPoint) Returns the result of adding two points Parameters: otherPoint - the point to be added to the receiver Returns: a Point object containing the sum of the two points distance public double distance(Point otherPoint) Returns the distance between two points Parameters: otherPoint - the point whose distance from the receiver is to be calculated Returns: a double representing the distance between the two points xReflection public Point xReflection() Returns the point obtained by a reflection of this point across the x-axis Returns: a Point object containing the reflection across the x-axis of this point yReflection public Point yReflection() Returns the point obtained by a reflection of this point across the y-axis Returns: a Point object containing the reflection across the y-axis of this point originReflection public point originReflection() Returns the point obtained by a reflection of this point through the origin Returns: a Point object containing the reflection of this point through the origin quadrant public int quadrant () Returns the quadrant (1,2,3,4, or 0) that this point resides in Returns: the quadrant this point resides in (1,2,3, or 4). If the point is the origin, 0 is returned. equals public boolean equals (Point otherPoint) Returns the result of checking the equality of two point -- two points are equal if their x and y coordinates are equal Parameters: otherpoint - the point to be checked for equality with the receiver Returns: true if the points are equal; false otherwise toString public java.lang.String tostring() Returns a string representation of the point in the form (x,y) Overrides: tostring in class java. lang. object Returns: the string representation read public static Point read(java.util.Scanner scanner) Returns a newly created Point object initialized with x,y values read from the scanner Parameters: quadrant public int quadrant() Returns the quadrant (1,2,3,4, or 0) that this point resides in Returns: the quadrant this point resides in (1,2,3, or 4). If the point is the origin, 0 is returned. equals public boolean equals(Point otherPoint) Returns the result of checking the equality of two point -- two points are equal if their x and y coordinates are equal Parameters: otherPoint - the point to be checked for equality with the receiver Returns: true if the points are equal; false otherwise tostring public java.lang. String tostring() Returns a string representation of the point in the form (x, y ) Overrides: tostring in class java. lang. Object Returns: the string representation read public static point read(java.util.Scanner scanner) Returns a newly created Point object initialized with x,y values read from the scanner Parameters: scanner - The Scanner used to read the point's initial values Returns: The newly created Point object











 Java
Java





