Jenkins Corporation is a major manufacturer of food processors. It purchases motors from Foster Corporation. Annual demand is 208,000 motors per year or 4,000 motors per week.
The ordering cost is $350 per order. The annual carrying cost is $9.10 per motor. It currently takes 3 weeks to supply an order to the assembly plant.

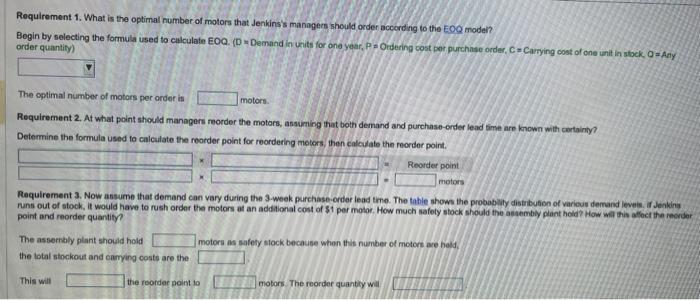
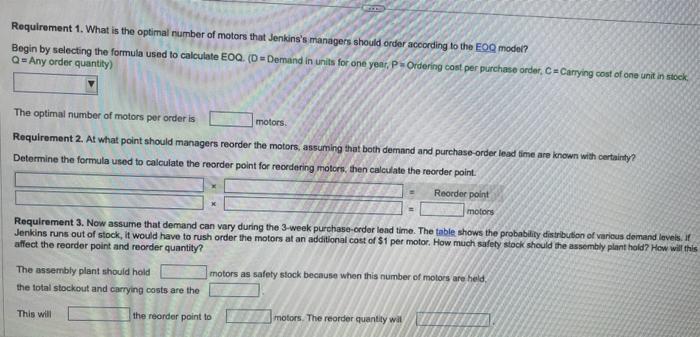
1. What is the optimal number of motors that Jenkins' managers should order according to the EOQ model? 2. At what point should managers reorder the motors, assuming that both demand and purchase-order lead time are known with certainty? 3. Now assume that demand can vary during the 3 -week purchase-order lead time. The following table shows the probability distribution of various demand levels: If Jenkins runs out of stock, it would have to rush order the motors at an additional cost of \$1 per motor. How much safety stock should the assembly plant hold? How will this affect the reorder point and reorder quantity? Requirement 1. What is the optimal number of motors that Jenkins's manogers should order according to the EOQ model? Begin by selecting the formula used to culculate EOQ. (D= Demand in units for one year, P= Ordering cost pot purchase order, C=Caying cost of one unit in stock, Q= Any order quantify) The optimal number of motors per order is motore. Requirement 2. At what point should managers reorder the motors, assuming that both demand and purchase-crder lead time are known with certainty? Determine the formula used to calculate the reorder point for reordering motors, then calculate the reorder point. runs out of atock, it would have to rush order the motors at an additional cost of $1 per motor. How much safely stock should the atsemby plant hold How will this affect the recrder point and reorder quantity? The assernbly plant should hold motors as safety stock because when this number of motort are hold, the lotal stockout and enmying costs are the This will the reorder point to miotors. The reorder quantly will Requirement 1. What is the optimal number of motors that Jenkins's managers should order according to the EOQ model? Begin by selecting the formula used to calculate EOQ. (D = Demand in units for one year, P= Ordering cost per parchase order, C=C Carrying cost of one unit in stock, Q= Any order quantity) The optimal number of motors per order is motors. Requirement 2. At what point should managers reorder the motors, assuming that both demand and purchase-order lead time are inown with certainty? Determine the formula used to calculate the reorder point for reordering motorn, then calculate the reorder point. Requirement 3. Now assume that demand can vary during the 3-week purchase-order lend time. The table shows the probability distrbubion of various demand lovels. if Jenkins runs out of stock, it would have to rush order the motors at an additional cost of $1 per motor. How much safety stock should the assembly piant hold? How will this affect the reorder point and reorder quantity? The assembly plant should hold motors as safety stock because when this number of motors are held. the total stockout and carrying costs are the This will the reorder point to motors. The reorder quantity wat