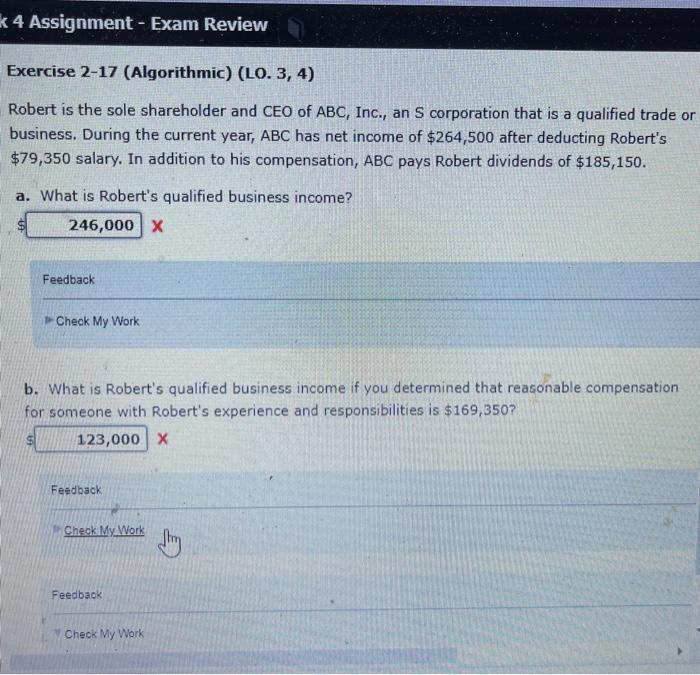
k 4 Assignment - Exam Review Exercise 2-17 (Algorithmic) (LO. 3, 4) Robert is the sole shareholder and CEO of ABC, Inc., an S corporation that is a qualified trade or business. During the current year, ABC has net income of $264,500 after deducting Robert's $79,350 salary. In addition to his compensation, ABC pays Robert dividends of $185,150. a. What is Robert's qualified business income? 246,000 X Feedback Check My Work b. What is Robert's qualified business income if you determined that reasonable compensation for someone with Robert's experience and responsibilities is $169,350? 123,000 X Feedback Check My Work Feedback Check My Work rate rj,.) Now if, because of exchange rate strangeness, rij Tji > 1, then you can make money simply by trading units of currency i into units of currency j and back again. (At least, if there are no exchange costs.) This almost never happens, but occasionally (because the updates for exchange rates do not happen quickly enough) for very short periods of time exchange traders can find a sequence of trades that can make risk-free money. That is, if there is a sequence of currencies C1, C2, Ci such that Ti,iz Tiz,is. Tik-1,ik Tikil > 1, then trading one unit of cinto C and trading that into Cia and so on back to C, will yield a profit. Design an efficient algorithm to detect if a risk-free currency exchange exists. (You need not actually find it.) 4. (20 points) Give an algorithm to find the lengths of all shortest paths from a given vertex in a directed graph G = (V,E) where all edge weights are integers between 0 and m, inclusive. Your algorithm should work in time O(|E| + |V|m). (Hint: Modify Dijkstra's algorithm.) 5. (15 points) Design an efficient algorithm to find the longest path in a directed acyclic graph whose edges have real-number weights. (Partial credit will be given for a solution where each edge has weight 1; full credit for solutions that handle general real-valued weights on the edges, including negative values.) Question 2: (9 Marks) A broker is trading his money in the stock market. Assume that the daily price of a specific stock along a certain period of time is given as follows: Price [200, 500, 800, 100, 300, 50] all in $. This means that the price of the stock is $200 in the first day, $500 in the second day, and so on. You are allowed to buy and sell the stock only once, which means that if you buy it on the 1st day (i.e. $200) and then sell it on the 3rd day (i.e. $800) a profit of $600 will be gained. You are requested to develop an algorithm to maximize the profit in single buy and sell. Another example: int prices = {300, 450, 720, 90, 30, 50, 900, 500, 70}; Output: Buying date: day 5, at the price of 30$ selling date: day 7, at the price of 900$ Maximum Profit: 870$ Answer the following questions: Short Term Exit Long Term Buy a) Design a brute force algorithm (pseudocode) to solve the above problem (1 mark), and determine its complexity (1 marks). b) Design an efficient algorithm (pseudocode) to solve the above problem (2 marks), and determine its complexity (1 marks). c) develop a brief report to explain the difference between the two algorithms and explain why one of them is more efficient than the other. (2 marks) d) Implement the efficient algorithm using Python (2 marks)