

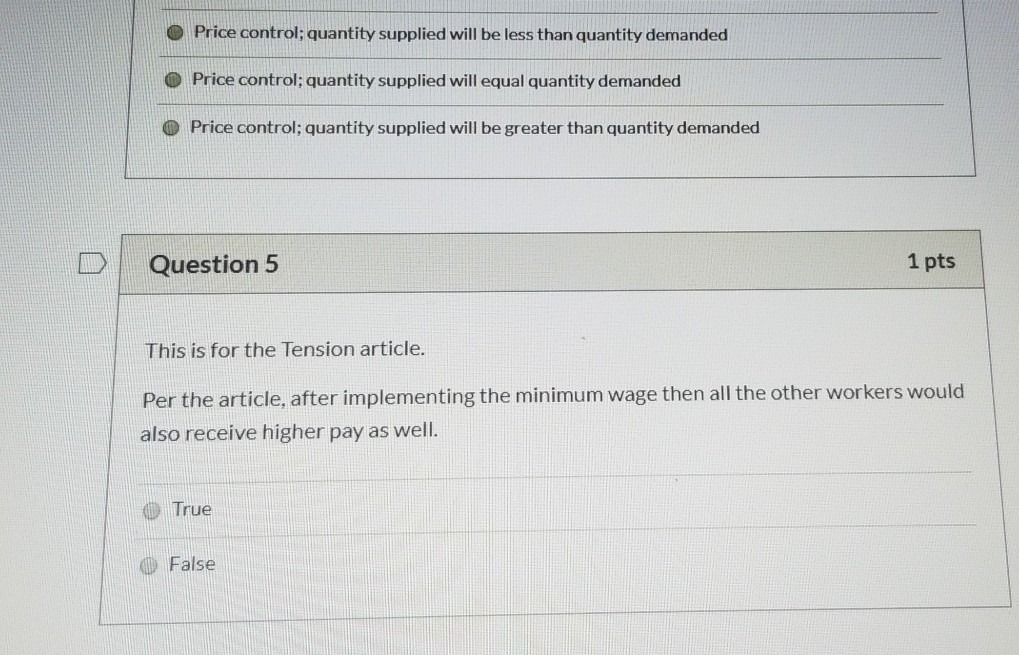
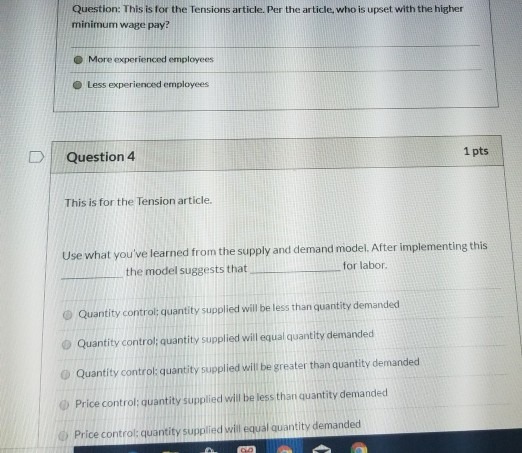

K kindly help me..
1. Suppose that there are two countries; Forwardia and Backwardia. Their production functions have the same Cobb-Douglas form as Y, = AK,"[e Li ]" where K, is capital, L; is the labor force, e, is the efficiency of labor and A, is the total factor productivity (TFP) of country i, where i E {F, B). We know that TFP of Forwardia is larger than that of Backwardia, i.e. AF > AB. The national saving rate s, the labor force growth rate n, the labor efficiency growth rate g and the capital depreciation rate o are all the same in both countries. (a) Start with the accumulation equation of aggregate capital K, for country i, and derive the accumulation equation of capital per effective worker k;. (You can assume that n.g is a very small, negligible value.) (b) Write an equation that describes the steady-state level of capital per effective worker for country i, i.e. kj. Considering that Ap > As, determine which country has higher capital per effective worker at the steady-state. Illustrate the steady-states of both countries on the same graph. Now (for parts (c), (d) and (e)) think about how these two countries transition towards steady-state. (You can refer to our lecture about convergence.) (c) Write down an equation for the growth rate of capital per effective worker for country i. The growth rate must be expressed as a difference of two values, which you will use next in part (d). (d) Show the growth rate of capital per effective worker for Forwardia and for Backwardia on the same graph, by plotting the two components of the growth rate equation you identified in part (c) over k, for both of the countries. (e) Assume that the current levels of capital per effective worker in both countries are below their steady-state levels, however ky > kg. First, determine which country currently has higher output per worker. Next, on the graph you drew in part (d), illustrate a case in which the richer country is growing faster than the poorer country. Finally, comment briefly on the convergence concept that is consistent with this particular case.Suppose that there are two countries; Forwardia and Backwardia. Their production functions have the same Cobb-Douglas form as Y, = Aik,"[el; ]17" where K is capital, L; is the labor force, e; is the efficiency of labor and A; is the total factor productivity (TFP) of country i, where i E {F, B). We know that TFP of Forwardia is larger than that of Backwardia, i.e. AF > Ap. The national saving rate s, the labor force growth rate n, the labor efficiency growth rate g and the capital depreciation rate o are all the same in both countries. (a) Start with the accumulation equation of aggregate capital K, for country i, and derive the accumulation equation of capital per effective worker k;- (You can assume that n.g is a very small, negligible value.) (b) Write an equation that describes the steady-state level of capital per effective worker for country i, i.e. kj. Considering that AF > AB, determine which country has higher capital per effective worker at the steady-state. Illustrate the steady-states of both countries on the same graph. Now (for parts (c), (d) and (e)) think about how these two countries transition towards steady-state. (You can refer to our lecture about convergence.) (c) Write down an equation for the growth rate of capital per effective worker for country i. The growth rate must be expressed as a difference of two values, which you will use next in part (d). (d) Show the growth rate of capital per effective worker for Forwardia and for Backwardia on the same graph, by plotting the two components of the growth rate equation you identified in part (c) over k, for both of the countries. (e) Assume that the current levels of capital per effective worker in both countries are below their steady-state levels, however ky > Kg. First, determine which country currently has higher output per worker. Next, on the graph you drew in part (d), illustrate a case in which the richer country is growing faster than the poorer country. Finally, comment briefly on the convergence concept that is consistent with this particular case.Suppose that there are two countries; Forwardia and Backwardia. Their production functions have the same Cobb-Douglas form as Y, = Aik,"[el; ]17" where K is capital, L; is the labor force, e; is the efficiency of labor and A; is the total factor productivity (TFP) of country i, where i E {F, B). We know that TFP of Forwardia is larger than that of Backwardia, i.e. AF > Ap. The national saving rate s, the labor force growth rate n, the labor efficiency growth rate g and the capital depreciation rate o are all the same in both countries. (a) Start with the accumulation equation of aggregate capital K, for country i, and derive the accumulation equation of capital per effective worker k;- (You can assume that n.g is a very small, negligible value.) (b) Write an equation that describes the steady-state level of capital per effective worker for country i, i.e. kj. Considering that AF > AB, determine which country has higher capital per effective worker at the steady-state. Illustrate the steady-states of both countries on the same graph. Now (for parts (c), (d) and (e)) think about how these two countries transition towards steady-state. (You can refer to our lecture about convergence.) (c) Write down an equation for the growth rate of capital per effective worker for country i. The growth rate must be expressed as a difference of two values, which you will use next in part (d). (d) Show the growth rate of capital per effective worker for Forwardia and for Backwardia on the same graph, by plotting the two components of the growth rate equation you identified in part (c) over k, for both of the countries. (e) Assume that the current levels of capital per effective worker in both countries are below their steady-state levels, however ky > Kg. First, determine which country currently has higher output per worker. Next, on the graph you drew in part (d), illustrate a case in which the richer country is growing faster than the poorer country. Finally, comment briefly on the convergence concept that is consistent with this particular case.Price control; quantity supplied will be less than quantity demanded O Price control; quantity supplied will equal quantity demanded Price control; quantity supplied will be greater than quantity demanded Question 5 1 pts This is for the Tension article. Per the article, after implementing the minimum wage then all the other workers would also receive higher pay as well. True FalseQuestion: This is for the Tensions article. Per the article, who is upset with the higher minimum wage pay? More experienced employees Less experienced employees D Question 4 1 pts This is for the Tension article. Use what you've learned from the supply and demand model. After implementing this the model suggests that for labor. Quantity control; quantity supplied will be less than quantity demanded Quantity control; quantity supplied will equal quantity demanded @Quantity control: quantity supplied will be greater than quantity demanded Price control; quantity supplied will be less than quantity demanded )Price control: quantity supplied will equal quantity demandedQ1: How is GE changing its business strategy and busines model? What is the role of information technology in GE's business *Please write at least at least 130 words to achieve high marks. Q2: On what business functions and level of decision making is GE focusing? *Please write at least at least 130 words to achieve high marks. Q3: Describe three kinds of decisions that can be supported using Predix. What is the value to the firm of each of those decisions? Explain. *Please write at least at least 130 words to achieve high marks
















