Karatsuba's algorithm multiplies two n-digit numbers using three multiplications of (n/2)-digit numbers and O(n) additional work, leading to the running time 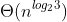. In general, for every 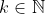, we can multiply two n-digit numbers using 2k-1 multiplications of (n/k)-digit numbers and O(n) additional work. Thus, for any value of k we can obtain a divide-and-conquer multiplication algorithm in the spirit of Karatsuba's algorithm. Using the master theorem, find the running time of this algorithm for an arbitrary choice of k. Show that, for every 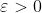, there is some value of k so that the running time is .

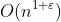I understand the part about the Master Theorem, but I am unsure what to make of the part about epsilon.

(nlog23 )