Ken and Larry, Inc., supplies its ice cream parlors with three flavors of ice cream: chocolate, vanilla, and banana. Due to extremely hot weather and a high demand for its products, the company has run short of its supply of ingredients: milk, sugar, and cream. Hence, they will not be able to fill all the orders received from their retail outlets, the ice cream parlors. Due to these circumstances, the company has decided to choose the amount of each flavor to produce that will maximize total profit, given the constraints on the supply of the basic ingredients. The chocolate, vanilla, and banana flavors generate, respectively, $1.00, $0.90, and $0.95 of profit per gallon sold. The company has only 200 gallons of milk, 150 pounds of sugar, and 60 gallons of cream left in its inventory. The linear programming formulation for this problem is shown below in algebraic form. Let C = Gallons of chocolate ice cream produced V = Gallons of vanilla ice cream produced B = Gallons of banana ice cream produced Maximize Profit = 1.00C + 0.90V + 0.95B subject to Milk: 0.45 C+0.50 V+0.40 B 200 gallons Sugar: 0.50 C+0.40 V+0.40 B 150 pounds Cream: 0.10 C+0.15 V+0.20 B 60 gallons and C0 V0 B0C0 V0 B0 This problem was solved using Solver. The spreadsheet (already solved) and the sensitivity report are shown below. (Note: The numbers in the sensitivity report for the milk constraint are missing on purpose, since you will be asked to fill in these numbers in part f.) For each of the following parts, answer the question as specifically and completely as possible without solving the problem again with Solver. Note: Each part is independent (i.e., any change made to the model in one part does not apply to any other parts).

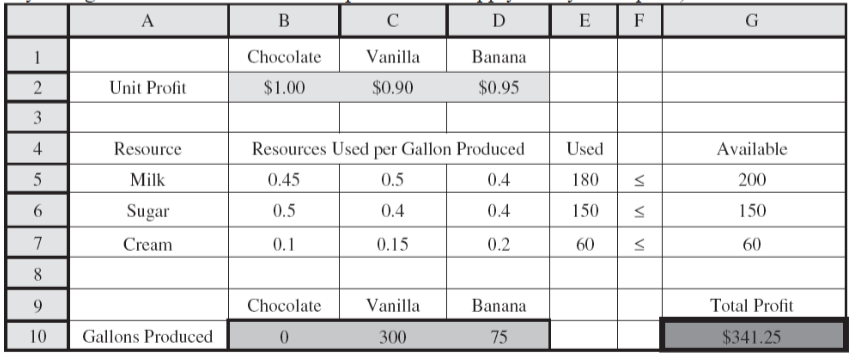
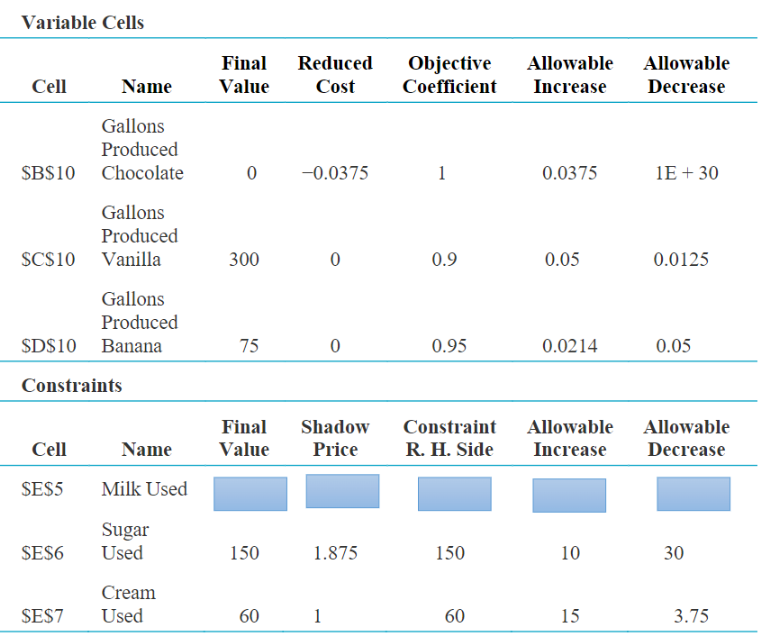
d. Suppose the company discovers that three gallons of cream have gone sour and so must be thrown out. Will the optimal solution change and what can be said about the effect on total profit? Explain and justify. e. Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15. Should it do so? Explain. f. Fill in all the sensitivity report information for the milk constraint, given just the optimal solution for the problem. Explain how you were able to deduce each number.

\begin{tabular}{|c|c|c|c|c|c|c|c|} \hline & A & B & C & D & E & F & G \\ \hline 1 & & Chocolate & Vanilla & Banana & & & \\ \hline 2 & Unit Profit & $1.00 & $0.90 & $0.95 & & & \\ \hline \multicolumn{8}{|l|}{3} \\ \hline 4 & Resource & \multicolumn{3}{|c|}{ Resources Used per Gallon Produced } & Used & & Available \\ \hline 5 & Milk & 0.45 & 0.5 & 0.4 & 180 & & 200 \\ \hline 6 & Sugar & 0.5 & 0.4 & 0.4 & 150 & & 150 \\ \hline 7 & Cream & 0.1 & 0.15 & 0.2 & 60 & & 60 \\ \hline \multicolumn{8}{|l|}{8} \\ \hline 9 & & Chocolate & Vanilla & Banana & & & Total Profit \\ \hline 10 & Gallons Produced & 0 & 300 & 75 & & & $341.25 \\ \hline \end{tabular} \begin{tabular}{|c|c|c|c|c|c|c|} \hline Cell & Name & FinalValue & ReducedCost & ObjectiveCoefficient & AllowableIncrease & AllowableDecrease \\ \hline SBS 10 & GallonsProducedChocolate & 0 & -0.0375 & 1 & 0.0375 & 1E+30 \\ \hline SCS10 & GallonsProducedVanilla & 300 & 0 & 0.9 & 0.05 & 0.0125 \\ \hline SD\$10 & GallonsProducedBanana & 75 & 0 & 0.95 & 0.0214 & 0.05 \\ \hline \multicolumn{7}{|c|}{ Constraints } \\ \hline Cell & Name & FinalValue & ShadowPrice & ConstraintR.H.Side & AllowableIncrease & AllowableDecrease \\ \hline SES5 & Milk Used & & & & & \\ \hline SES6 & SugarUsed & 150 & 1.875 & 150 & 10 & 30 \\ \hline SES7 & CreamUsed & 60 & 1 & 60 & 15 & 3.75 \\ \hline \end{tabular}