Kindly solve the following sample difference questions

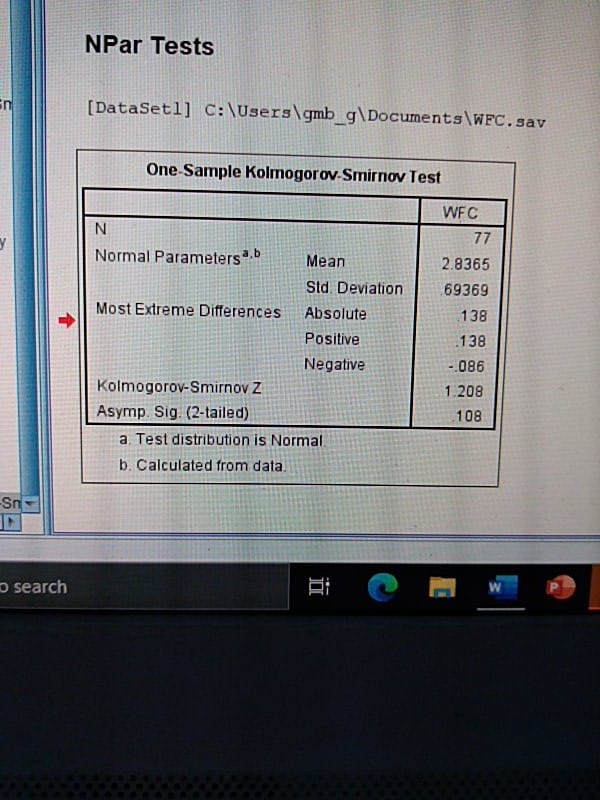
11. Kolmogorov-Lilliefors Test | Exercises due Aug 5, 2020 08:59 KST W Bookmark this page Motivation: Goodness of Fit Testing for a Gaussian Distribution 1 point possible (graded) Let X1, ..., Xn be iid random variables with continuous cdf F. Let {N (u, ") ) ,ER,62> denote the family of all Gaussian distributions. We want to test whether or not FE IN (1, )) HER,a320 Let @,02 denote the cdf of N (1, of). We formulate the null and alternative hypotheses Ho : F = Pu,o2for some H E R, oz > 0 H1 : F # @u,02for any H E R, o- > 0. Motivated by the Kolmogorov-Smirnov test, you define a test-statistic using the sample mean / and sample variance o2: T n = sup Vn| Fn(1) - Q. Hod. Assume that the null hypothesis is true. Is it true that (a) Tn - sup |B (x) | where B (x) is a Brownian bridge? (Refer to the slides.) O True O FalseNPar Tests [DataSet]] C: \\Users\\gmb g\\Documents\\WFC. sav One-Sample Kolmogorov-Smirnov Test WFC N 77 Normal Parameters .b Mean 2.8365 Sid Deviation 69369 Most Extreme Differences Absolute 138 Positive 138 Negative ..086 Kolmogorov-Smirnov Z 1 208 Asymp Sig. (2-tailed) 108 a. Test distribution is Normal b. Calculated from data. Sn search W6. ( 6 pts ) Consider the following symmetric matrix: 1 1 A=1 11 1 1 1 Compute the spectral decomposition of A = QAQwhere Q is an orthogonal matrix and A a diagonal matrix.1. (a) Explain what is meant by the transition probability matrix of a homogeneous Markov chain. [5 marks] (b) Explain what is meant by the stationary distribution of a Markov chain? [5 marks] (c) A Markov chain has transition probability matrix, A, with entries ay, and stationary distribution . Write down an expression for the entries of the reverse Markov chain. [5 marks (d) Consider the following transition probability matrix of a homogo- neous Markov chain, with three states i,j and & (the TPM is in that order). If the stationary vector of the chain is (1/9, 2/9, 2/3), determine whether the Markov chain is reversible. 1 Ik 1- /0.2 0.2 0.6 0.1 0.6 0.3 K 0.1 0.1 0.8 [5 marks] (e) Let X1, X2, X, be a sequence of random variables resulting from the above Markov chain. If X = i and Xy = j what is the probability that X2 = k? [5 marks]