lathu2nd

please answer all in step by step manner. please dont give wrong answer. thank you.

q1:

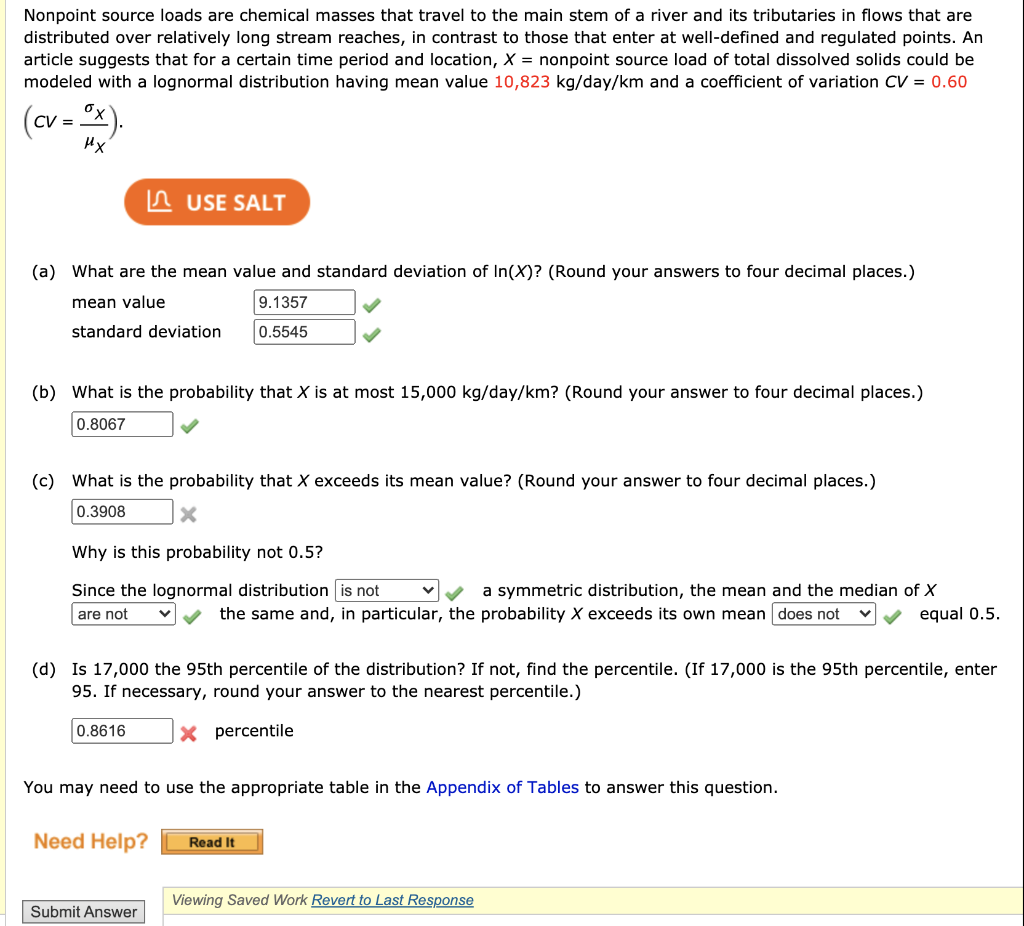
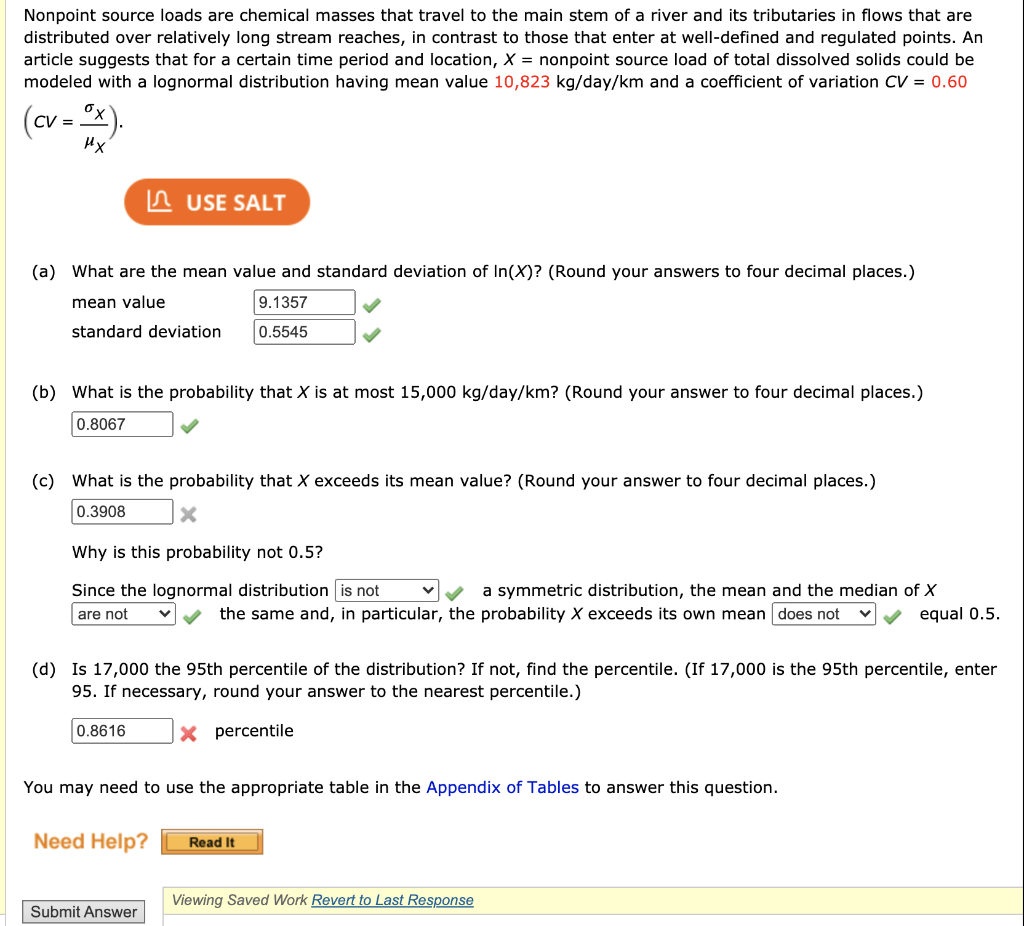
Formulas: x-bar i m phat 1r m estimate i m phat = x I n p = X I N x-bar i T (s 1 xi?) p-hat i z \\l p-hat (1 p-hat) I n Use the formulas to solve: 3) The city has 10,983 voters. Joe samples 375 of them. Their mean interest level in politics is 4.386 with standard deviation 0.521 [the scale was from 0 to 10]. 168 of them say they support Freddy for mayor. Use 96% confidence when needed. a) What percentage of all city voters support Freddy for mayor? How many voters would that be? Looking at this result, does it seem he could win the election? Explain. b) What is the average level of interest in politics of city voters? c) Are the conditions for parts a) and b) met? d) For part a) what sample size would reduce the margin of error to .035, approximately? (15 marks) (a) Compute a test of the proposition that students' cumulative Grade Point Average has no effect on students' final exam grade. State the coefficient restrictions on regression equation (1) implied by this proposition; that is, state the null hypothesis Ho and the alternative hypothesis H1. Write the restricted regression equation implied by the null hypothesis Ho. OLS estimation of this restricted regression equation yields an RZ = 0.1701. Use this information, together with the results from OLS estimation of equation (1), to calculate the required test statistic. State the decision rule you use, and the inference you would draw from the test at the 5 percent significance level. (15 marks) (b) The average student in the course has a cumulative Grade Point Average of 2.5; that is, the sample mean value of GPA, equals 2.5. Write the expression (or formula) for the marginal effect on finalpet, of GPA, implied by regression equation (1). Use the estimation results for regression equation (1) to test the proposition that the marginal effect of cumulative GPA (GPA;) on students final exam grade (finalpet,) equals zero for the average student whose GPA is 2.5. State the null and alternative hypotheses, and show how you calculate the required test statistic. State the inference you would draw from the test at the 5 percent significance level. (15 marks) (c) Use the estimation results for regression equation (1 ) to test the joint significance of the slope coefficient estimates , (j = 1, ...,4) in regression equation (1). Perform the test at the 5 percent significance level (i.e., for significance level a = 0.05). State the null and alternative hypotheses, and show how you calculate the required test statistic. State the inference you would draw from the test at the 5 percent significance level.Question 2 (45 marks) You are investigating the relationship between the final exam grades of university students in an introductory economics course and those students' class attendance, as measured by the percentage of classes each student attended during the term. You also have sample data on two additional explanatory variables: each student's cumulative GPA (Grade Point Average) prior to the term in which the introductory economics course was taken; and each student's score on a standardized college entrance exam, the ACT exam. You have sample data for 680 students on the following variables: finalpet, = final exam grade of the i-th student, measured in percentage points; attrate, = percentage of classes attended by the i-th student during the term, measured in percentage points; GPA = Cumulative Grade Point Average (GPA) of the i-th student prior to the term in which the introductory economics course was taken, measured out of 4.0; ACT, = ACT score of the i-th student on the ACT college entrance exam, measured in points. Using the given sample data on 680 students, your trusty research assistant has estimated regression equation (1) and obtained the following estimation results (with estimated standard errors given in parentheses below the coefficient estimates): finalpet, = Bo + Blattrate; + B2GPA; + B3GPA; + BAACT + us (1) Bo = 55.564 B1 = 0.071698 B2 = -18.6518 (8.077) (0.0279) (5.5788) B3 = 4.4785 BA = 0.9 (1.0513) (0.1336) Cov(B1.B2) = -0.024 Cov(B1.B3) = 0.00203 Cov( B1,B4) = 0.001284 Cov(B2,B3) =-5.7846 Cov(B2. B4) = 0.075667 cov(B3,B4) = -0.025335 SSR = 73218.11 SST = 94137.17 N = 680 SSR is the Residual Sum-of-Squares and SST is the Total Sum-of-Squares for sample regression equation (1). Sample size N = 680. Cov(Bj, Bn) is the estimated covariance between coefficient estimates , and An. Estimated standard errors are given in parentheses below the coefficient estimates B, (j = 0,1, ...,4)Nonpoint source loads are chemical masses that travel to the main stem of a river and its tributaries in flows that are distributed over relatively long stream reaches, in contrast to those that enter at well-defined and regulated points. An article suggests that for a certain time period and location, X = nonpoint source load of total dissolved solids could be modeled with a lognormal distribution having mean value 10,823 kg/day/km and a coefficient of variation CV = 0.60 CV = _ HX LO USE SALT (a) What are the mean value and standard deviation of In(X)? (Round your answers to four decimal places. ) mean value 9.1357 standard deviation 0.5545 (b) What is the probability that X is at most 15,000 kg/day/km? (Round your answer to four decimal places.) 0.8067 (c) What is the probability that X exceeds its mean value? (Round your answer to four decimal places.) 0.3908 X Why is this probability not 0.5? Since the lognormal distribution |is not vy a symmetric distribution, the mean and the median of X are not the same and, in particular, the probability X exceeds its own mean |does not v equal 0.5. (d) Is 17,000 the 95th percentile of the distribution? If not, find the percentile. (If 17,000 is the 95th percentile, enter 95. If necessary, round your answer to the nearest percentile.) 0.8616 * percentile You may need to use the appropriate table in the Appendix of Tables to answer this question. Need Help? Read It Submit Answer Viewing Saved Work Revert to Last ResponseConsider two fair dice: The first is 6 sided (X=1,2,3,4,5,6) and the second is 4 sided (Y=1,2,3,4). a. Determine the probability mass function (pmf) of each random variable (Separately). (5 points) b. Determine the moment generating function (mgf) of each random variable (10 points). C. Consider a board game that is played by rolling these two dices at each round and the players move according to the sum of the two dices (Z=X+Y). The possible values of Z are (2,3,4,5,6,7,8,9,10). Use the moment generating functions of these two discrete random variables to find the moment generating function of Z. (5 points) d. Use the mef of Z to find the probabilities for each of the values of Z (in other words, what is the distribution of Z, or the pmf of Z). (5 points) e. Use the mgf of Z to find the expected value of Z. (5 points) f. Use the pmf of Z to find the expected value of Z. (5 points)A sample of 26 offshore oil workers took part in a simulated ricape exercise, Inviting in the accompanying dots on tome [rec) to complete the ricope. 173 374 371 354 365 344 325 398 304 192 359 375 359 35 403 334 198 A normal probably plot of the of a 26 observations on cicaps time gives above shows a substantial new patters; The sample mein and simple standard deviation are 3/1 00 and 24 54, respectively. (Round your aramer to two decimal Co) Calculate an upper confidence bound for population mean evoige time aging a confidence level of gym Q) Calculate an woper production bound for the suraje time of a single add tiond worter ming s prediction level of 18% How done this boand compare win the onidente bound of pan toy The upper profusion found is boomer pas the upper confidenie bound O The upper prodicon bound is equal to the the opper mooddance bound The upper prediction bound is higher than the upper confidence bound. (c) Suppow that two additional workers will be choup to participate in the simulated tocape exercise, Denote their escape times by My, and $, and let AGances the average of theme two values. Modify the formula for a It for a single # value to obtain a Pl for &. . and calculate a 95% top-sided interval based on the gres civice data. You may need to use the appropriate table In the Append op answer this purtion.Suppose the brightness of Pyralis fireflies (lightning bugs) when they glow at night is Normally distributed with a mean of approximately 0.314 lumens and a standard deviation of approximately 0.08 lumens. a. Sketch and clearly label the Normal model for the brightness of these fireflies, based on the 68-95-99.7 Rule. Be sure to label your axis with what the variable represents. b. What percentage of these fireflies do we expect to have a brightness less than 0.3 lumens? (To show your work: Write down which calculator/program you are using and what values you are entering into the calculator.) c. Find the cutoff brightness levels for the middle 50% of these fireflies. Include units in your answer. (To show your work: Write down which calculator/ program you are using and what values you are entering into the calculator.) d. Give the mean and standard deviation of the Normal model that would be used to approximate the sampling distribution of the sample mean for a random sample of 25 fireflies. Include units in your answers. e. Find the probability that a random sample of 25 fireflies has an average brightness less than 0.3 lumens. (To show your work: Write down which calculator/program you are using and what values you are entering into the calculator.}