Let p(1),...,p(n) be prices of a stock for n consecutive days. A k-shot strategy is a collection of m pairs of days (b1,s1),...,(bm,sm) with 0 ? m ? k and1 ? b1

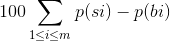
Design a Dynamic Programming algorithm that takes as input the prices of the n consecutive days, p(1), . . . , p(n) and for some k computes the maximum return among all k-shot strategies. (Hint: Your subproblems should be indexed by two indices.) (best runtime: O(n2k) or better)

1. Decription of subproblem

2. Base Case

3. Subproblem expressed recursively

4. The ordering of the subproblems. (The for loop(s) of the iteration.)

5. What does the algorithm return?

100 100 p(si) (si) bi) p(bi) m