Let X be a set of n intervals on the real line. A subset of intervals Y X is called a full path if the intervals in Y cover the intervals in X, that is, any real value that is contained in some interval in X is also contained in some interval in Y . The size of the full path is the number of intervals it contains.

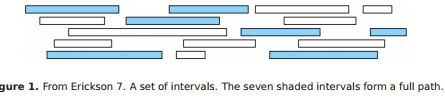
Describe and analyze a greedy algorithm to compute the smallest full path of X as quickly as possible. Assume that your input consists of two arrays XL [1..n] and XR [1..n], representing the left and right endpoints of the intervals in X. Dont forget to prove your greedy algorithm is correct!

pseudocode is fine