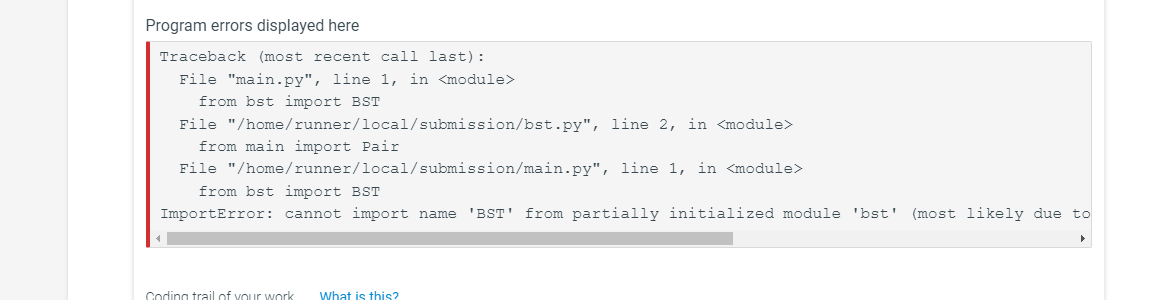
Question: Main.py From here, bst.py The introduction is here from bst import BST class Pair: '.' Encapsulate letter, count pair as a single entity. Realtional methods
Main.py
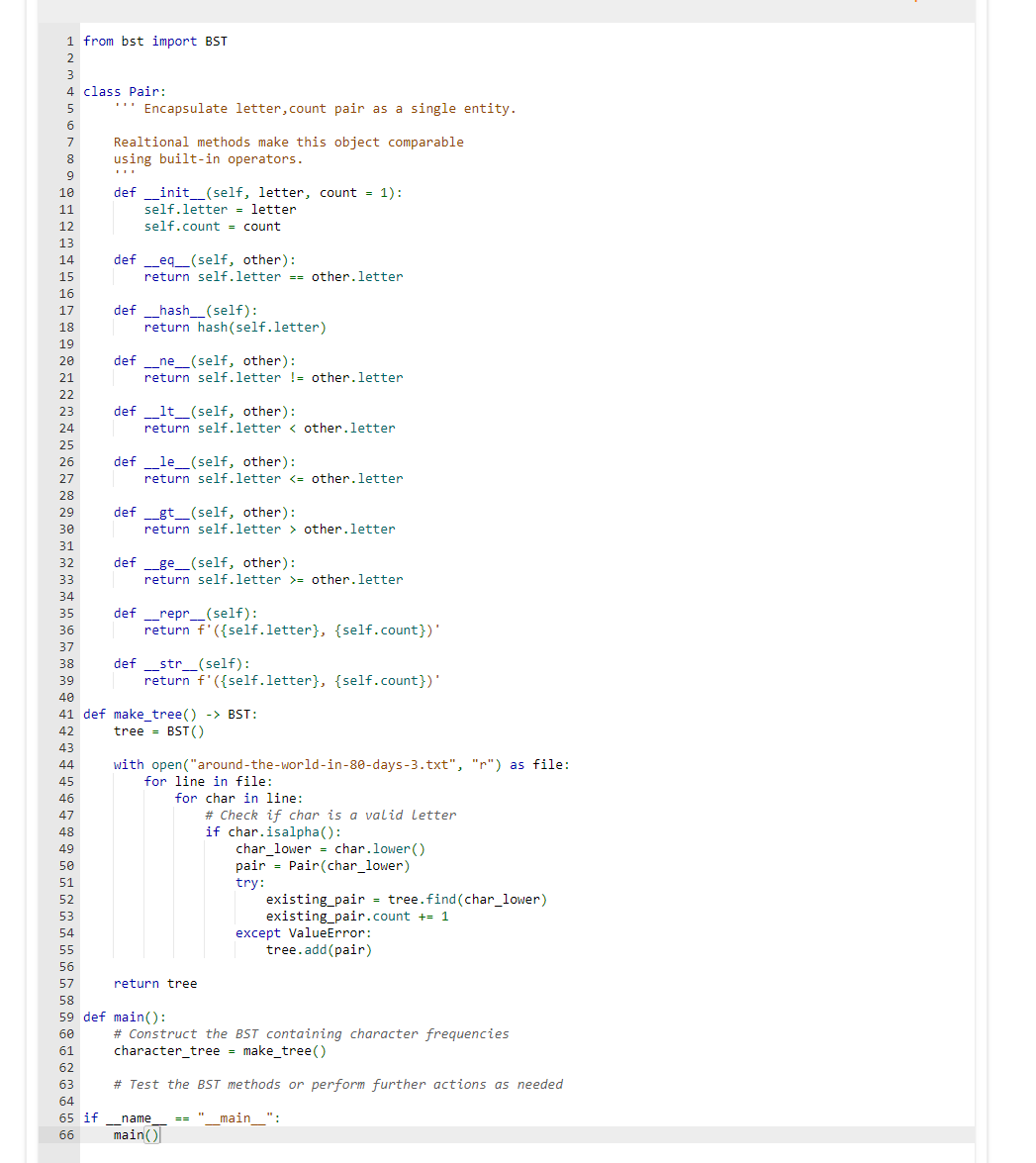
From here, bst.py
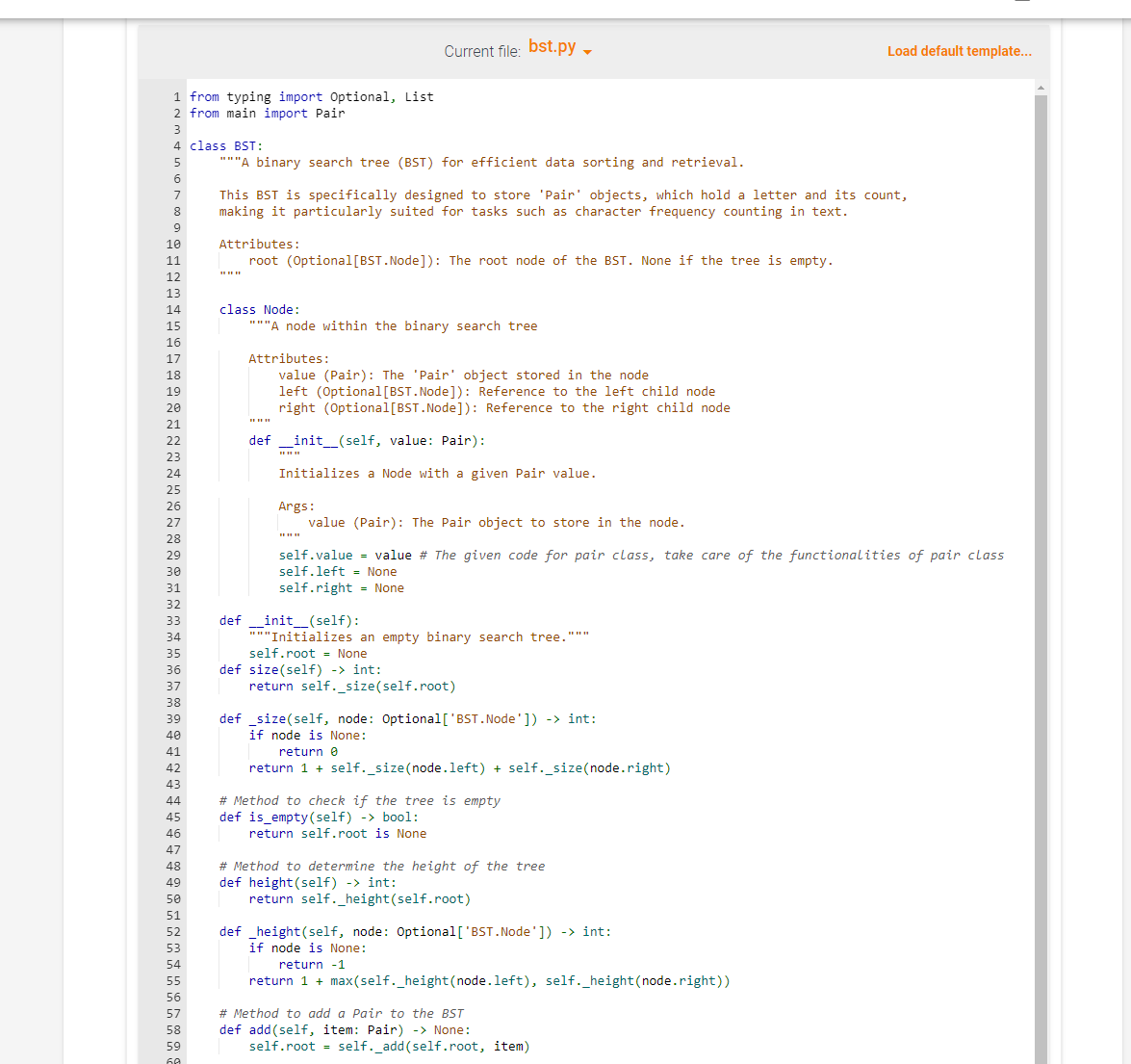
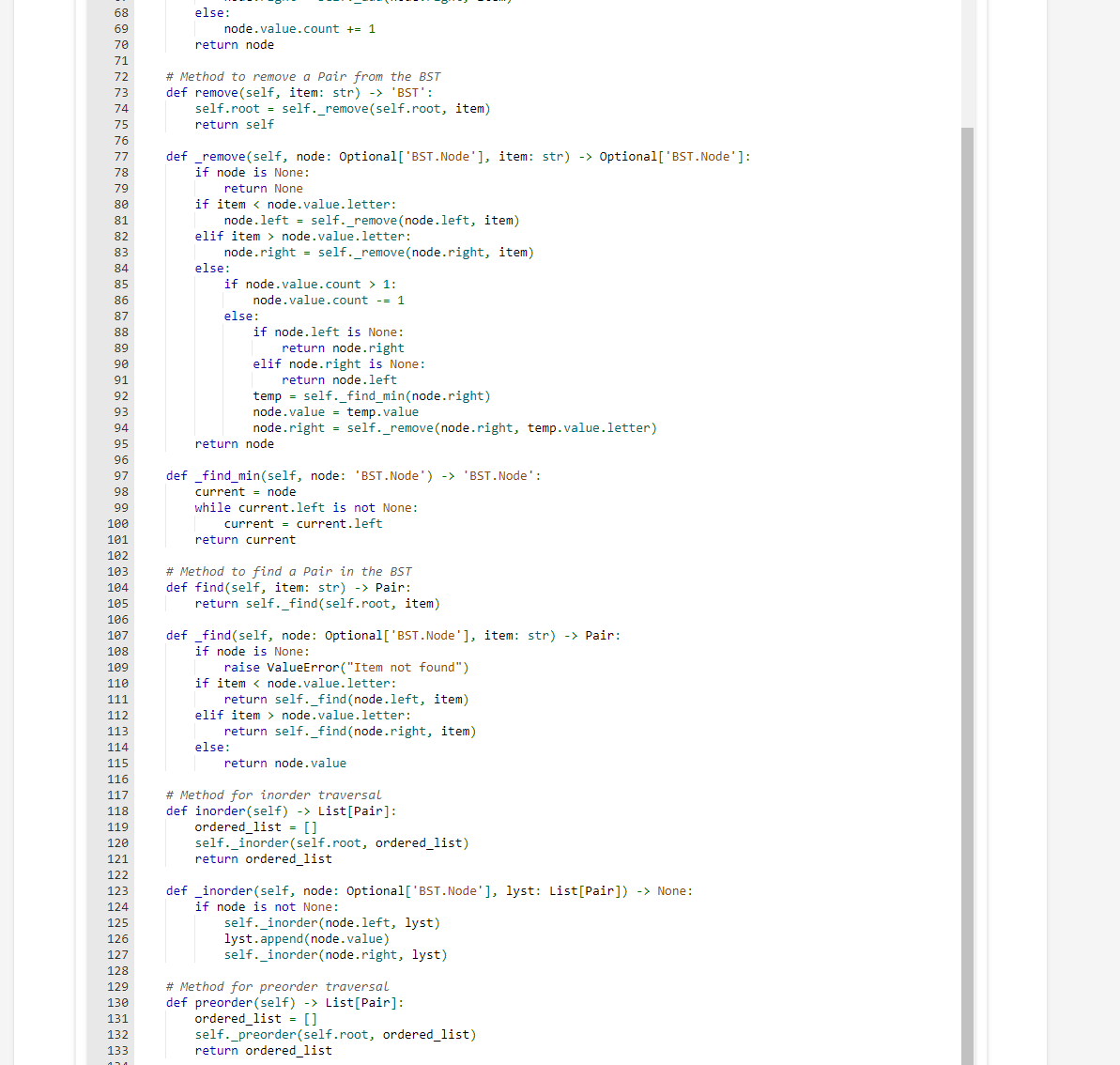
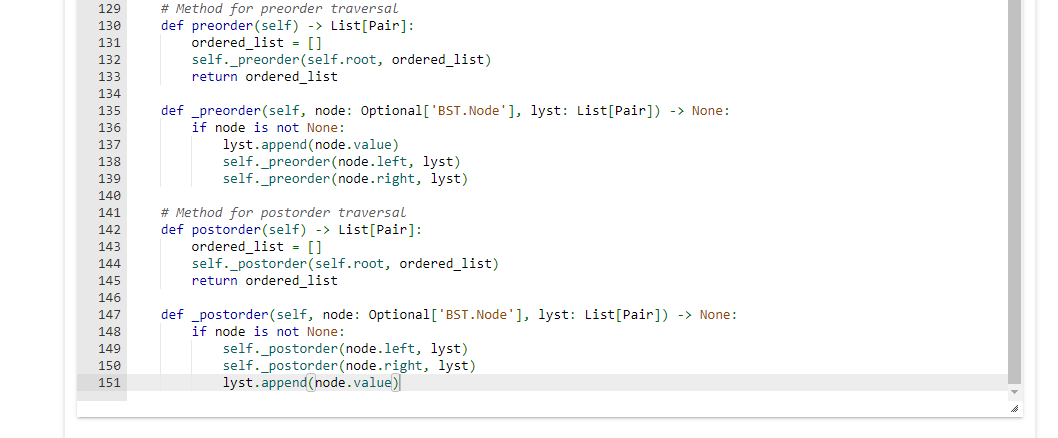
The introduction is here

from bst import BST class Pair: '.' Encapsulate letter, count pair as a single entity. Realtional methods make this object comparable using built-in operators. ,.. def __init__(self, letter, count =1) : self.letter = letter self.count = count def __eq_(self, other): return self.letter == other. letter def __hash__(self): return hash(self.letter) def _ne_(self, other): return self.letter != other.letter def __lt_(self, other): return self.letter other.letter def _-ge_(self, other): return self.letter >= other.letter def __repr__(self): return f({ self.letter }, self.count }) def __str__(self): return f({self.letter},{self.count}) def make_tree() BST: tree = BST () with open("around-the-world-in-80-days-3.txt", "r") as file: for line in file: for char in line: \# Check if char is a valid letter if char.isalpha(): char_lower = char.lower ( ) pair =Pair(char_lower) try: existing_pair = tree.find (char_lower) existing_pair.count +=1 except ValueError: tree.add (pair) return tree def main(): \# Construct the BST containing character frequencies character_tree = make_tree () \# Test the BST methods or perform further actions as needed om typing import Optional, List rom main import Pair lass BST: """A binary search tree (BST) for efficient data sorting and retrieval. This BST is specifically designed to store 'Pair' objects, which hold a letter and its count, making it particularly suited for tasks such as character frequency counting in text. Attributes: root (Optional[BST.Node]): The root node of the BST. None if the tree is empty. class Node: "" A node within the binary search tree Attributes: value (Pair): The 'Pair' object stored in the node left (Optional[BST.Node]): Reference to the left child node right (Optional[BST.Node]): Reference to the right child node n"n def __init__(self, value: Pair): Initializes a Node with a given Pair value. Args: value (Pair): The Pair object to store in the node. self.value = value \# The given code for pair class, take care of the functionalities of pair class self.left = None self.right = None def__init__(self): "" Initializes an empty binary search tree."" self. root = None def size(self) int: return self._size(self.root) def _size(self, node: Optional['BST.Node']) int: if node is None: return return 1 + self._size(node.left) + self._size(node.right) \# Method to check if the tree is empty def is_empty(self) bool: return self.root is None \# Method to determine the height of the tree def height(self) int: return self._height(self.root) def _height(self, node: Optional['BST.Node']) -> int: if node is None: return -1 return 1+max( self._height(node.left), self._height(node.right)) \# Method to add a Pair to the BST def add(self, item: Pair) None: self , root = self , add ( self , root, item ) else: node. value. count t=1 return node \# Method to remove a Pair from the BST def remove(self, item: str) 'BST': self.root = self._remove ( self.root, item) return self def _remove(self, node: Optional['BST.Node'], item: str) Optional['BST.Node']: if node is None: return None if item = self._remove (node.left, item) elif item > node.value. letter: node. right = self.. remove ( node.right, item ) else: if node.value.count >1 : node. value. count =1 else: if node.left is None: return node.right elif node.right is None: return node. left temp = self._find_min(node.right) node .value = temp .value node. right = self._remove (node.right, temp.value.letter ) return node def _find_min(self, node: 'BST.Node') 'BST.Node': current = node while current.left is not None: current = current. left return current \# Method to find a Pair in the BST def find(self, item: str) Pair: return self._find(self.root, item) def _find(self, node: Optional['BST.Node'], item: str) Pair: if node is None: raise ValueError("Item not found") if item > node.value.letter: return self._find(node.right, item) else: return node.value \# Method for inorder traversal def inorder(self) List[Pair]: ordered_list =[] self._inorder(self.root, ordered_list) return ordered_list def _inorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: if node is not None: self._inorder(node.left, lyst) lyst. append (node.value) self._inorder(node.right, lyst) \# Method for preorder traversal def preorder(self) List[Pair]: ordered_list =[] self._preorder(self.root, ordered_list) return ordered_list \# Method for preorder traversal def preorder(self) List[Pair]: ordered_list =[] self._preorder(self.root, ordered_list) return ordered_list def _preorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: if node is not None: lyst.append(node.value) self._preorder(node.left, lyst) self._preorder(node.right, lyst) \# Method for postorder traversal def postorder(self) List[Pair]: ordered_list =[] self._postorder(self.root, ordered_list) return ordered_list def _postorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: if node is not None: self._postorder(node.left, lyst) self._postorder(node.right, lyst) lyst.append(node.value) Program errors displayed here Traceback (most recent call last): File "main.py", line 1, in from bst import BST File "/home/runner/local/submission/bst.py", line 2, in from main import Pair File "/home/runner/local/submission/main.py", line 1, in from bst import BST ImportError: cannot import name 'BST' from partially initialized module 'bst' (most likely due to Project 6: Binary Search Tree Duration: 8 hours Reminder: Read through this entire project description before you begin working on it. Introduction Natural language processing (NLP) involves leveraging the power of computing systems to analyze natural languages (such as those we speak or write) to determine things like meaning, authorship, etc. Some of the most important advances in NLP occurred when computer scientists realized that statistics could be used to derive and predict a great deal about natural languages - even without an understanding of what is written or said. Of course every good statistic begins with the act of counting something - consequently, an important and common task in NLP is the act of counting things like letters and words. It is desirable that such counting can be performed efficiently, and the results accessed quickly. A binary search tree offers us the ability to do both. In this lab you will construct and utilize a binary search tree to compile character frequency counts from a sample text. (Note: we consider the digits 0-9 to be characters along with the letters of the alphabet) In CS 1400, you may recall, you learned how to do word counts using a dictionary-this problem is similar, only we are counting characters, not words, and we are building our own key, value data structure vs using the built-in dictionary type. Note: This is a fancy way of saying that you can NOT utilize Python's dictionary type Yes, there are a number of ways in Python to do this exercise that don't require us to write much code of our own-but a lot of high-powered databases and search engines use some form of tree structure to store and retrieve dynamic data fast, and here we get a peek under the hood. This is, after all why you're in this class. Part 1: BST Not surprisingly, your first task will be to create a binary search tree ADT as a class called BST. You should implement this class in a file called bst.py. Your ADT must implement the following methods: - size(): Return the number of nodes in the tree. - is_empty(): Return True if there aren't any nodes in the tree, False otherwise. - height(): Return the height of the tree, defined is the length of the path from the root to its deepest leaf. A tree with zero nodes has a height of -1 . - add(item): Add item to its proper place in the tree. Return the modified tree. - remove(item): Remove item from the tree if it exists, if not - do nothing. Return the resulting tree. - find(item): Return the matched item from the tree (not the node that contains it, and not the item used as the parameter). If item is not in the tree, raise a ValueError. - inorder(): Return a list with the data items in order of inorder traversal. - preorder(): Return a list with the data items in order of preorder traversal. - postorder(): Return a list with the data items in order of postorder traversal. - [Optional] print_tree(): print the values in the tree (in any way you wish). Useful for debugging purposes (a good example of this can be found in section 5.12.1 under the TreePrint.py file). Your BST class must be generic is the sense that it can store and operate on any kind of data items that are comparable. For instance it should be possible to store a set of integers in one instance of your BST class, and a set of strings in another (without modification). Part 2: Counting with trees For part 2 of this project you are to use your BST to count the occurrence of letters in a sample test file (note: for our purposes we will NOT consider whitespace characters - you should ignore tabs, spaces, and newlines). To do this you will need to be able to store both a character and its current count in the tree. One way to do this is to utilize a simple class that stores both of these values, and is comparable on one of them (i.e. you can compare objects of the class using > other.letter def _-ge_(self, other): return self.letter >= other.letter def __repr__(self): return f({ self.letter }, self.count }) def __str__(self): return f({self.letter},{self.count}) def make_tree() BST: tree = BST () with open("around-the-world-in-80-days-3.txt", "r") as file: for line in file: for char in line: \# Check if char is a valid letter if char.isalpha(): char_lower = char.lower ( ) pair =Pair(char_lower) try: existing_pair = tree.find (char_lower) existing_pair.count +=1 except ValueError: tree.add (pair) return tree def main(): \# Construct the BST containing character frequencies character_tree = make_tree () \# Test the BST methods or perform further actions as needed om typing import Optional, List rom main import Pair lass BST: """A binary search tree (BST) for efficient data sorting and retrieval. This BST is specifically designed to store 'Pair' objects, which hold a letter and its count, making it particularly suited for tasks such as character frequency counting in text. Attributes: root (Optional[BST.Node]): The root node of the BST. None if the tree is empty. class Node: "" A node within the binary search tree Attributes: value (Pair): The 'Pair' object stored in the node left (Optional[BST.Node]): Reference to the left child node right (Optional[BST.Node]): Reference to the right child node n"n def __init__(self, value: Pair): Initializes a Node with a given Pair value. Args: value (Pair): The Pair object to store in the node. self.value = value \# The given code for pair class, take care of the functionalities of pair class self.left = None self.right = None def__init__(self): "" Initializes an empty binary search tree."" self. root = None def size(self) int: return self._size(self.root) def _size(self, node: Optional['BST.Node']) int: if node is None: return return 1 + self._size(node.left) + self._size(node.right) \# Method to check if the tree is empty def is_empty(self) bool: return self.root is None \# Method to determine the height of the tree def height(self) int: return self._height(self.root) def _height(self, node: Optional['BST.Node']) -> int: if node is None: return -1 return 1+max( self._height(node.left), self._height(node.right)) \# Method to add a Pair to the BST def add(self, item: Pair) None: self , root = self , add ( self , root, item ) else: node. value. count t=1 return node \# Method to remove a Pair from the BST def remove(self, item: str) 'BST': self.root = self._remove ( self.root, item) return self def _remove(self, node: Optional['BST.Node'], item: str) Optional['BST.Node']: if node is None: return None if item = self._remove (node.left, item) elif item > node.value. letter: node. right = self.. remove ( node.right, item ) else: if node.value.count >1 : node. value. count =1 else: if node.left is None: return node.right elif node.right is None: return node. left temp = self._find_min(node.right) node .value = temp .value node. right = self._remove (node.right, temp.value.letter ) return node def _find_min(self, node: 'BST.Node') 'BST.Node': current = node while current.left is not None: current = current. left return current \# Method to find a Pair in the BST def find(self, item: str) Pair: return self._find(self.root, item) def _find(self, node: Optional['BST.Node'], item: str) Pair: if node is None: raise ValueError("Item not found") if item > node.value.letter: return self._find(node.right, item) else: return node.value \# Method for inorder traversal def inorder(self) List[Pair]: ordered_list =[] self._inorder(self.root, ordered_list) return ordered_list def _inorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: if node is not None: self._inorder(node.left, lyst) lyst. append (node.value) self._inorder(node.right, lyst) \# Method for preorder traversal def preorder(self) List[Pair]: ordered_list =[] self._preorder(self.root, ordered_list) return ordered_list \# Method for preorder traversal def preorder(self) List[Pair]: ordered_list =[] self._preorder(self.root, ordered_list) return ordered_list def _preorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: if node is not None: lyst.append(node.value) self._preorder(node.left, lyst) self._preorder(node.right, lyst) \# Method for postorder traversal def postorder(self) List[Pair]: ordered_list =[] self._postorder(self.root, ordered_list) return ordered_list def _postorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: if node is not None: self._postorder(node.left, lyst) self._postorder(node.right, lyst) lyst.append(node.value) Program errors displayed here Traceback (most recent call last): File "main.py", line 1, in from bst import BST File "/home/runner/local/submission/bst.py", line 2, in from main import Pair File "/home/runner/local/submission/main.py", line 1, in from bst import BST ImportError: cannot import name 'BST' from partially initialized module 'bst' (most likely due to Project 6: Binary Search Tree Duration: 8 hours Reminder: Read through this entire project description before you begin working on it. Introduction Natural language processing (NLP) involves leveraging the power of computing systems to analyze natural languages (such as those we speak or write) to determine things like meaning, authorship, etc. Some of the most important advances in NLP occurred when computer scientists realized that statistics could be used to derive and predict a great deal about natural languages - even without an understanding of what is written or said. Of course every good statistic begins with the act of counting something - consequently, an important and common task in NLP is the act of counting things like letters and words. It is desirable that such counting can be performed efficiently, and the results accessed quickly. A binary search tree offers us the ability to do both. In this lab you will construct and utilize a binary search tree to compile character frequency counts from a sample text. (Note: we consider the digits 0-9 to be characters along with the letters of the alphabet) In CS 1400, you may recall, you learned how to do word counts using a dictionary-this problem is similar, only we are counting characters, not words, and we are building our own key, value data structure vs using the built-in dictionary type. Note: This is a fancy way of saying that you can NOT utilize Python's dictionary type Yes, there are a number of ways in Python to do this exercise that don't require us to write much code of our own-but a lot of high-powered databases and search engines use some form of tree structure to store and retrieve dynamic data fast, and here we get a peek under the hood. This is, after all why you're in this class. Part 1: BST Not surprisingly, your first task will be to create a binary search tree ADT as a class called BST. You should implement this class in a file called bst.py. Your ADT must implement the following methods: - size(): Return the number of nodes in the tree. - is_empty(): Return True if there aren't any nodes in the tree, False otherwise. - height(): Return the height of the tree, defined is the length of the path from the root to its deepest leaf. A tree with zero nodes has a height of -1 . - add(item): Add item to its proper place in the tree. Return the modified tree. - remove(item): Remove item from the tree if it exists, if not - do nothing. Return the resulting tree. - find(item): Return the matched item from the tree (not the node that contains it, and not the item used as the parameter). If item is not in the tree, raise a ValueError. - inorder(): Return a list with the data items in order of inorder traversal. - preorder(): Return a list with the data items in order of preorder traversal. - postorder(): Return a list with the data items in order of postorder traversal. - [Optional] print_tree(): print the values in the tree (in any way you wish). Useful for debugging purposes (a good example of this can be found in section 5.12.1 under the TreePrint.py file). Your BST class must be generic is the sense that it can store and operate on any kind of data items that are comparable. For instance it should be possible to store a set of integers in one instance of your BST class, and a set of strings in another (without modification). Part 2: Counting with trees For part 2 of this project you are to use your BST to count the occurrence of letters in a sample test file (note: for our purposes we will NOT consider whitespace characters - you should ignore tabs, spaces, and newlines). To do this you will need to be able to store both a character and its current count in the tree. One way to do this is to utilize a simple class that stores both of these values, and is comparable on one of them (i.e. you can compare objects of the class using >
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


