MATLAB: All of the information is being provided for the sake of context, however I only need help writing the loops for problem two. Although advice/help on how to get the final function within the tolerances specified for the end of part one would be appreciated as well.


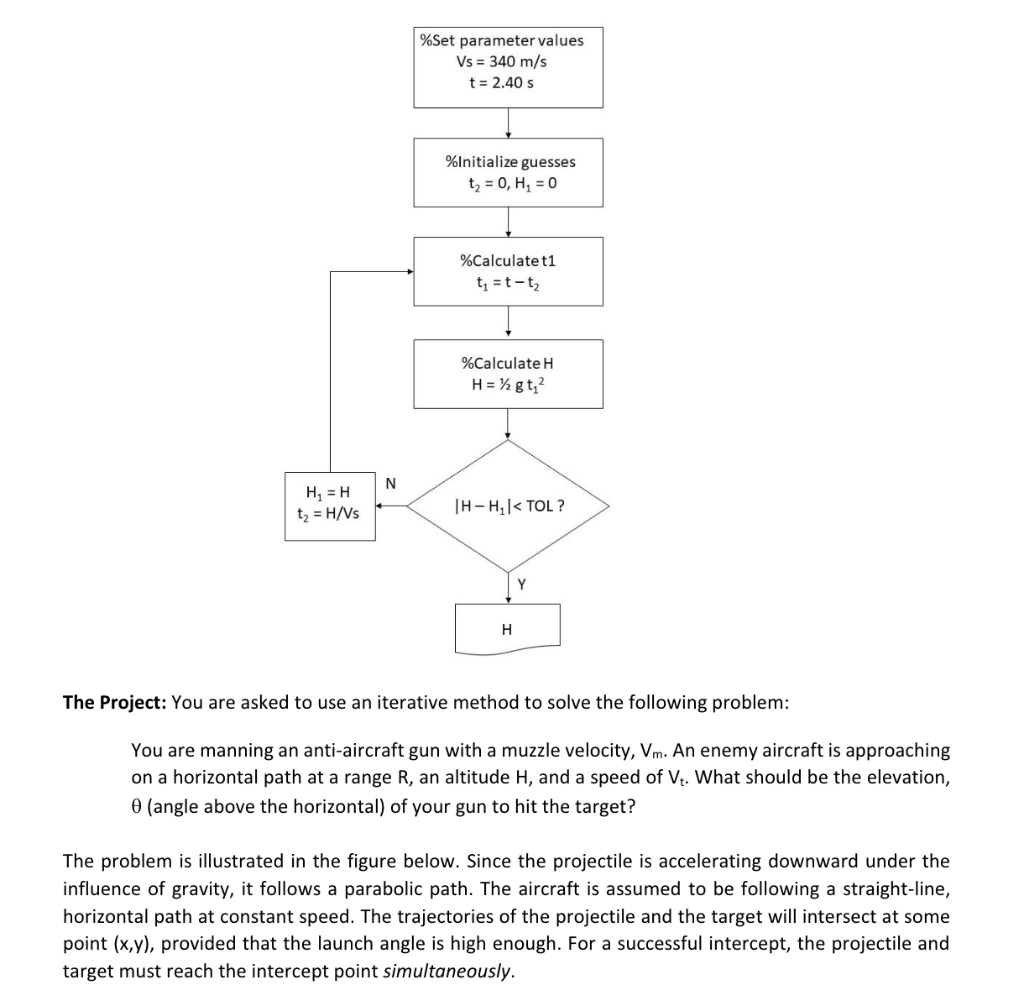
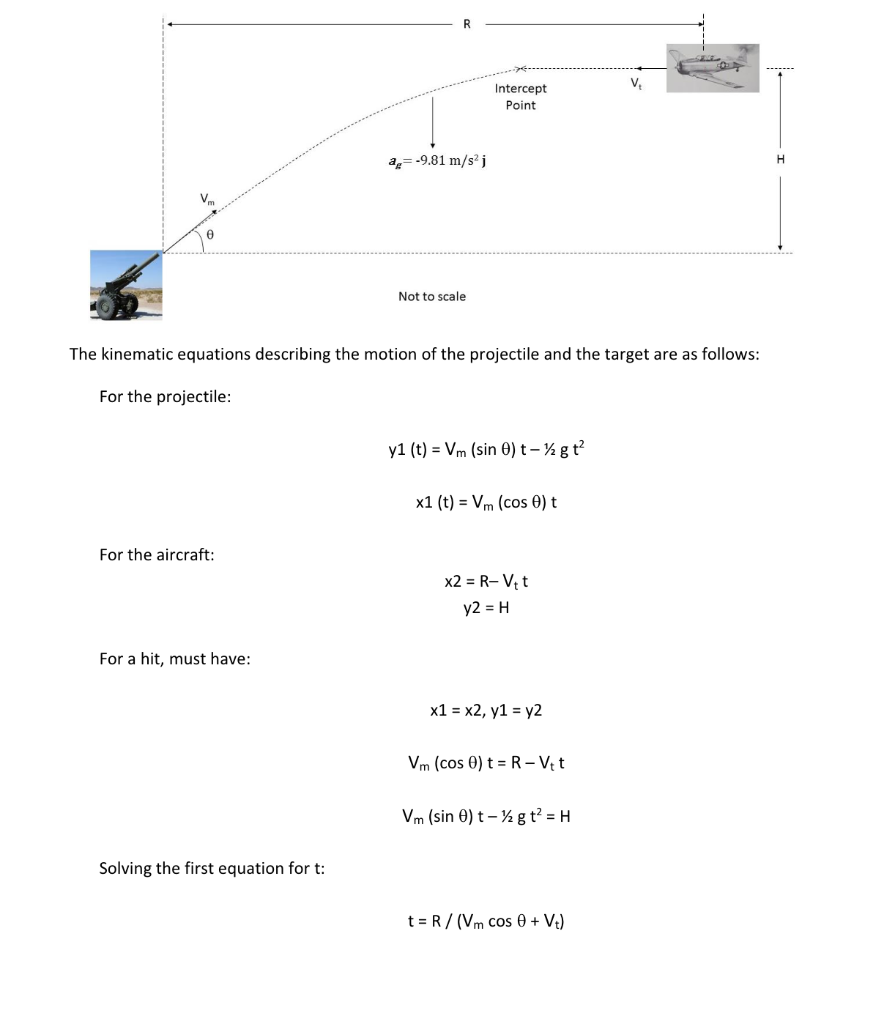


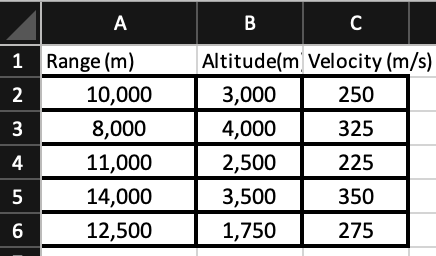
Background: Iterative Solution to Mechanics Problems In introductory physics, most problems can be solved algebraically, partly because simplifying assumptions are used (no air resistance, small-angle approximation, etc.). When more detailed and realistic descriptions of the physics are incorporated into a problem, it may not be solvable in closed form. In cases like this, numerical solutions are sought. One technique for solving problems numerically is iteration. An iterative solution proceeds as follows: make an initial assumption, or guess, about the solution apply this assumption to generate a first, approximate solution adopt the approximate solution as the new guess, and use it to calculate a second approximation continue this process, generating better and better approximations, until the solution converges that is, until the next iteration does not change the solution significantly Depending on the complexity of the problem, iterative solutions may or may not produce an accurate solution efficiently, independent of the initial guess. The problems that we are tackling in this assignment are amenable to an iterative approach - if your code is correct, you will get a good solution in a small number of iterations, regardless of your initial guess. Example: Accounting for the finite speed of sound Consider this problem: A man drops a rock into a well. He hears the sound of the splash 2.40 s after he releases the rock from rest. How far below the top of the well is the surface of the water? The reason that this problem is not as trivial as it seems is that 2.40 s is not the time that it takes for the rock to hit the water, but rather the time that it takes for the echo to reach the top of the well. That is, it is the sum of the time for the rock to hit the water (ta) and the time for the echo to travel to the top of the well (tz). Although this problem can in fact be solved exactly, it is nonetheless a good example to illustrate the iterative method. First approximation The starting assumption is that the time for the echo to travel to the top of the well is small compared to the time for the rock to hit the water. The first approximation for the depth of the well can therefore be calculated from simple kinematics as follows: Ay = Vot-12 gt? where g = 9.81 m/s2 is the acceleration due to gravity at the surface of the earth. Since the rock is dropped, not thrown, Vo = 0, and H=Ay= 12 gt2 = 12 (9.81 m/s) (2.40s)2 = 28.25 m Second approximation Given this initial estimate for the depth of the well, the time for the echo to propagate to the top, assuming speed of sound = 340 m/s, is t2 = (28.25 m)/(340 m/s) = 0.083 s This implies that the time for the rock to reach the water was not the full 2.40 s, but rather t1 = 2.40 s - 0.083 s = 2.317 s Therefore, a better estimate of the depth of the well is H = 72 gt? = 72 (9.81 m/s2) (2.3175)2 = 26.33 m Of course, the process does not stop here. Based on this improved estimate for H, we can get a better estimate for t2, which leads to an even better estimate for H, and so on. Eventually, assuming that the calculation converges, the difference between subsequent estimates of H will be negligibly small. In this example, H converges within 5 iterations to a final value of 26.45 m. A logical diagram (flow chart) of this algorithm is shown below. This algorithm can be implemented using a while loop. The loop terminates when two subsequent approximations for the result (H and H1) differ by less than a specified tolerance (TOL). %Set parameter values Vs = 340 m/s t = 2.40 S %Initialize guesses ta = 0, H = 0 %Calculate t1 t = t-tz %Calculate H H = gt; H = H t2 = H/Vs TH-Hy













