matlab code. This question is based on (but is not identical to) exercise 13 on page 121 of the textbook. This problem models a short polymer molecule (Figure 4.4 on page 121) as a system of springs and of masses which are free to move only in the x-direction. For ease of marking, in the Figure: * Label the masses 0 to 3 from left to right. * Assume that mass 0 is always located at x0 = 0. * Label the springs as follows: * spring 1 connects masses 0 and 1; * spring 2 connects masses 0 and 2; * spring 3 connects masses 1 and 2; * spring 4 connects masses 1 and 3; * spring 5 connects masses 2 and 3. a) [10 points] Submit your answer in PDF format for this part of the question. As discussed in section 4.2, set up the system of equations for x1, x2, and x3 in this problem. (x0 is treated as a constant, not a variable, and is set equal to zero.) In matrix notation, this system of equations is abbreviated as F = Kx b where F is the vector of net forces on the masses. Derive K and b for the general case where all springs have different spring constants ki and different rest lengths Li . You must show your work in going from the net force equations to the matrix form for the system of equations to receive any credit for this question. Your answer should reduce to the following K and b for the special case in which all springs have rest length 1, springs 1 and 5 have spring constant k1, and springs 2, 3 and 4 have spring constant k2. K = 2k2 k1 k2 k2 k2 2k2 k1 k1 k2 k1 k2 k1 ; b = 2k2 k1 2k2 + k1 k2 k1 b) [30 points] Turn in a single .m format MATLAB program and a single JPG format figure for this part of the question. Write a program which runs as a function from the command line to find the equilibrium positions of the masses as a function of k1/k2 by solving Kx = b for the special case above. As always, you must comment your code! You must include an example of how to run your program that the TA can just cut and paste into the MATLAB command window to run the program and produce your submitted plot. Your program must plot the equilibrium positions of all four masses on the same figure as a function of k1/k2 for the special case above. Your plot must have a title including your name, must include clear axis labels, must use a logarithmic axis where appropriate, and must cover a sufficient range in k1/k2 to make clear any limiting values of the total length of the polymer. Tip: do the mass positions and the total polymer length make sense for (k1/k2) 1, k1/k2 = 1, and (k1/k2) 1? If not, check your code!

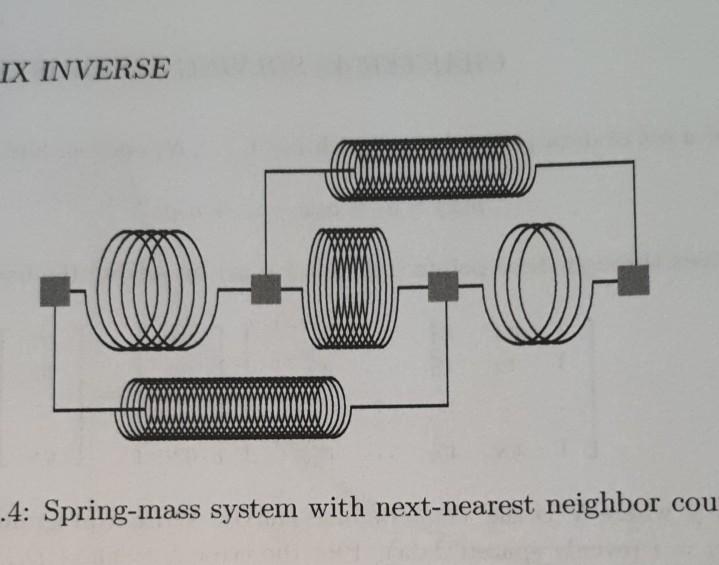
This question is based on (but is not identical to) exercise 13 on page 121 of the textbook. This problem models a short polymer molecule (Figure 4.4 on page 121) as a system of springs and of masses which are free to move only in the 2-direction. For ease of marking, in the Figure: * Label the masses 0 to 3 from left to right. * Assume that mass 0 is always located at .co = 0. * Label the springs as follows: * spring 1 connects masses 0 and 1; * spring 2 connects masses 0 and 2; * spring 3 connects masses 1 and 2: * spring 4 connects masses 1 and 3; spring 5 connects masses 2 and 3. a) [10 points] Submit your answer in PDF format for this part of the question. As discussed in section 4.2, set up the system of equations for 11, 12, and x3 in this problem. (xo is treated as a constant, not a variable, and is set equal to zero.) In matrix notation, this system of equations is abbreviated as F = Kx - b where F is the vector of net forces on the masses. Derive K and b for the general case where all springs have different spring constants k, and different rest lengths L. You must show your work in going from the net force equations to the matrix form for the system of equations to receive any credit for this question. Your answer should reduce to the following K and b for the special case in which all springs have rest length 1, springs 1 and 5 have spring constant ki, and springs 2, 3 and 4 have spring constant ka. [- 2k2-ki ky kr 2k2-ki K= -2k-k ky b 1-2kz+ki kz -ky-k] -kiz-ki b) [30 points] Turn in a single .m format MATLAB program and a single JPG format figure for this part of the question. Write a program which runs as a function from the command line to find the equilibrium positions of the masses as a function of ks/ky by solving Kx=b for the special case above. As always, you must comment your code! You must include an example of how to run your program that the TA can just cut and paste into the MATLAB command window to run the program and produce your submitted plot. Your program must plot the equilibrium positions of all four masses on the same figure as a function of ki/ky for the special case above. Your plot must have a title including your name, must include clear axis labels, must use a logarithmic axis where appropriate, and must cover a sufficient range in ki/k to make clear any limiting values of the total length of the polymer. Tip: do the mass positions and the total polymer length make sense for (ky/ky) 1? If not, check your code! IX INVERSE 0 .4: Spring-mass system with next-nearest neighbor cou 13. Consider the spring-mass system in Figure 4.4 (a simple model of a short poly- mer molecule). The blocks are free to move but only along the I-axis. The springs connecting adjacent blocks have spring constant k, while the two outer springs have stiffness ka. All the springs have a rest length of one. (a) Write the matrix equation for the equilibrium positions of the blocks. (Pencil] (b) Write a program that plots the total length of the system as a function of ki/k2. (Computer] 14. Consider utama 13) with N - 1 blocks. This question is based on (but is not identical to) exercise 13 on page 121 of the textbook. This problem models a short polymer molecule (Figure 4.4 on page 121) as a system of springs and of masses which are free to move only in the 2-direction. For ease of marking, in the Figure: * Label the masses 0 to 3 from left to right. * Assume that mass 0 is always located at .co = 0. * Label the springs as follows: * spring 1 connects masses 0 and 1; * spring 2 connects masses 0 and 2; * spring 3 connects masses 1 and 2: * spring 4 connects masses 1 and 3; spring 5 connects masses 2 and 3. a) [10 points] Submit your answer in PDF format for this part of the question. As discussed in section 4.2, set up the system of equations for 11, 12, and x3 in this problem. (xo is treated as a constant, not a variable, and is set equal to zero.) In matrix notation, this system of equations is abbreviated as F = Kx - b where F is the vector of net forces on the masses. Derive K and b for the general case where all springs have different spring constants k, and different rest lengths L. You must show your work in going from the net force equations to the matrix form for the system of equations to receive any credit for this question. Your answer should reduce to the following K and b for the special case in which all springs have rest length 1, springs 1 and 5 have spring constant ki, and springs 2, 3 and 4 have spring constant ka. [- 2k2-ki ky kr 2k2-ki K= -2k-k ky b 1-2kz+ki kz -ky-k] -kiz-ki b) [30 points] Turn in a single .m format MATLAB program and a single JPG format figure for this part of the question. Write a program which runs as a function from the command line to find the equilibrium positions of the masses as a function of ks/ky by solving Kx=b for the special case above. As always, you must comment your code! You must include an example of how to run your program that the TA can just cut and paste into the MATLAB command window to run the program and produce your submitted plot. Your program must plot the equilibrium positions of all four masses on the same figure as a function of ki/ky for the special case above. Your plot must have a title including your name, must include clear axis labels, must use a logarithmic axis where appropriate, and must cover a sufficient range in ki/k to make clear any limiting values of the total length of the polymer. Tip: do the mass positions and the total polymer length make sense for (ky/ky) 1? If not, check your code! IX INVERSE 0 .4: Spring-mass system with next-nearest neighbor cou 13. Consider the spring-mass system in Figure 4.4 (a simple model of a short poly- mer molecule). The blocks are free to move but only along the I-axis. The springs connecting adjacent blocks have spring constant k, while the two outer springs have stiffness ka. All the springs have a rest length of one. (a) Write the matrix equation for the equilibrium positions of the blocks. (Pencil] (b) Write a program that plots the total length of the system as a function of ki/k2. (Computer] 14. Consider utama 13) with N - 1 blocks