MGHW5 for more info:
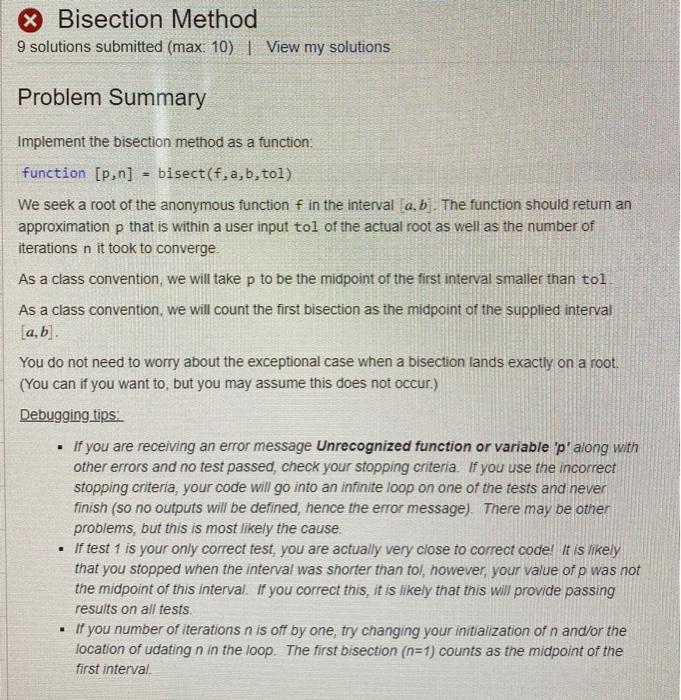
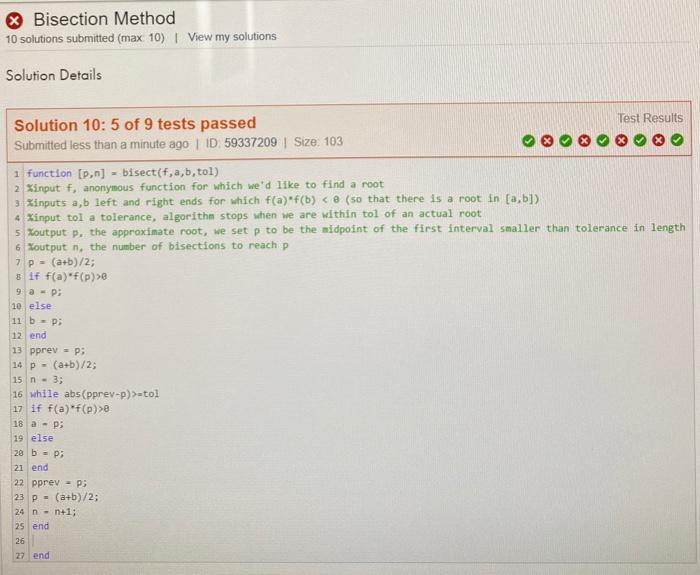
Bisection Method:
Newton's Method:
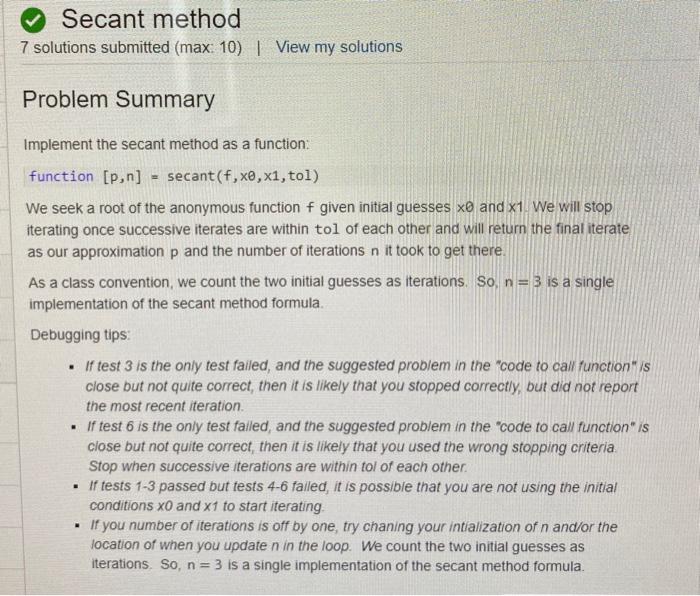
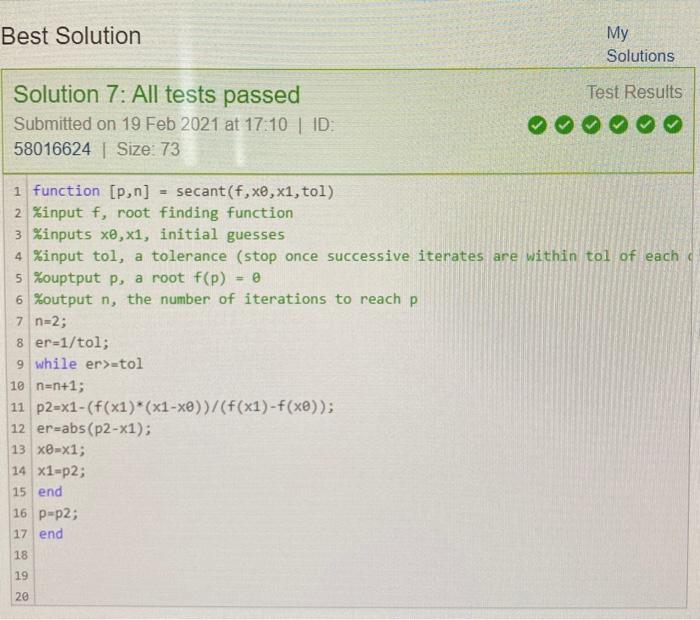
Secant Method:
This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the following steps: Download your complete and correct algorithms (bisect.m, my Newton.m, and secant.m) from MGHW5 and save it to your own computer in a folder called Root Finding. Do not change the code in any of these three files! Open a new (driver) script m-file to complete the problems on this homework assignment. Call the functions you wrote. If you need to compute something like error (which is not an output of the algorithms), don't change the algorithms. Get the outputs and then manipulate them in your driver script. In conjunction with your driver script, refer to your handwritten notes about the algorithms to answer the "math" parts of the questions. 72 2. This problem will be completed in class on Monday 2/22. The function f(x) = (x-3) has one root, r* = 3. Starting with an initial guess x1 = 2, Newton's method generates the following sequence of approximations to r*. In error 12.0000 2 2.5000 3 2.7500 4 2.8750 5 2.9375 (a) (1 point) Fill in the error column of the table. Use a driver script to generate the data! (b) (1 point) Determine the order of convergence a associated to this test problem. Show your work to get the final computation. Continue to use the driver script! (e) (1 point) What facts about f(x) let you predict the convergence rate for this instance of Newton's method (without knowing the data in the table above)? X Bisection Method 9 solutions submitted (max: 10) | View my solutions Problem Summary Implement the bisection method as a function: function [p, n] = bisect(f, a, b, tol) We seek a root of the anonymous function f in the interval (a, b The function should retum an approximation p that is within a user input tol of the actual root as well as the number of iterations n it took to converge. As a class convention, we will take p to be the midpoint of the first interval smaller than tol As a class convention, we will count the first bisection as the midpoint of the supplied interval [a, b]. You do not need to worry about the exceptional case when a bisection lands exactly on a root. (You can if you want to, but you may assume this does not occur.) Debugging tips: If you are receiving an error message Unrecognized function or variable 'p' along with other errors and no test passed, check your stopping criteria. If you use the incorrect stopping criteria, your code will go into an infinite loop on one of the tests and never finish (so no outputs will be defined, hence the error message). There may be other problems, but this is most likely the cause. If test 1 is your only correct test, you are actually very close to correct code! It is likely that you stopped when the interval was shorter than tol, however, your value of p was not the midpoint of this interval. If you correct this, it is likely that this will provide passing results on all tests if you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. The first bisection (n=1) counts as the midpoint of the first interval . X Bisection Method 10 solutions submitted (max 10) | View my solutions Solution Details Test Results Solution 10: 5 of 9 tests passed Submitted less than a minute ago ID 59337209 Size: 103 1 function (p.n] - bisect(f, a, b, tol) 2 Xinput f, anonymous function for which we'd like to find a root 3 Xinputs a,b left and right ends for which f(a) f(b) 9 - P 10 else 11 b =D 12 end 13 pprev = P: 14 P- (a+b)/2 15 n-3; 16 while abs(pprev->-tol 17 if f(a) f(p) > 18 a- Di 19 else 20 b-pi 21 end 22 pprev - Pi 23 p = (a+b)/2; 24 n - n+1; 25 end 26 27 end Newton's Method 10 solutions submitted (max: 10) | View my solutions Problem Summary Implement Newton's method as a function function [P,n] = myNewton(f,fprime,xe,tol) We seek a root of the anonymous function f given an initial guess xo. We input f and its derivative fprime. We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p. Also output the number of iterations n it took to reach p As a class convention, we say that the initial guess counts as 1 iteration So, in a sense, n=2 would mean we took one step of Newton's method. Debugging tips If test 3 is the only test passed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other. if tests 1 and 7 are the only tests failed, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration . If your code failed to complete, with this message. Your code could not run to completion, possibly due to an out-of-memory condition. Common causes are either loading large files or a missing ";" from the end of a command.If the problem persists, contact the instructor, it is possible that you are not using the initial condition xo to start iterating in addition to the suggestion made by Matiad of using If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. We say that the initial guess is n = 1. So, in a sense n=2 would mean we took one step of Newton's method . Best Solution My Solutions Test Results Solution 9: 7 of 8 tests passed Submitted on 19 Feb 2021 at 23:44 | ID. 58075754 Size: 67 1 function [P,n] = myNewton(f,fprime ,xe,tol) 2 Xinput f, anonymous function for root finding problem 3 %input fprime, anonlymous function, the derivative of f 4 Linput xe, an initial guess 5 %input tol, a tolerance (method will stop when successive iterates are within 1 6 Zoutput p, a root f(p) = 7 Zoutput n, the number of iterations to reach p 8 n-1; 9 P = 99; 10 while(abs (P-XO)>-tol) p=0; 12 n=n+1; 13 b=(xe*fprime(xe))-f(xe); 14 x =(roots([fprime(x),-b])); 15 end 16 P=x0; 17 end 11 18 Secant method 7 solutions submitted (max 10) | View my solutions Problem Summary Implement the secant method as a function function [p, n] = secant(f,x0, x1, tol) We seek a root of the anonymous function f given initial guesses x@ and X1. We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p and the number of iterations n it took to get there. As a class convention, we count the two initial guesses as iterations. So, n= 3 is a single implementation of the secant method formula Debugging tips If test 3 is the only test failed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration If test 6 is the only test falled, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other . If tests 1-3 passed but tests 4-6 failed, it is possible that you are not using the initial conditions x0 and x1 to start iterating If you number of iterations is off by one, try chaning your intialization of n and/or the location of when you update n in the loop. We count the two initial guesses as iterations. So, n=3 is a single implementation of the secant method formula. Best Solution My Solutions Test Results Solution 7: All tests passed Submitted on 19 Feb 2021 at 17:10 | ID: 58016624 | Size: 73 1 function [2,n] = secant(f,xe, x1, tol) 2 %input f, root finding function 3 %inputs xe, x1, initial guesses 4 %input tol, a tolerance (stop once successive iterates are within tol of each 5 %ouptput p, a root f(p) = 0 6 %output n, the number of iterations to reach p 7 n=2; 8 er=1/tol; 9 while er>=tol 10 n=n+1; 11 p2=x1-(f(x1)*(x1-x))/(F(x1)-f(xe)); 12 er-abs (p2-x1); 13 x0=1; 14 x1=p2; 15 end 16 p-p2; 17 end 18 19 2e This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the following steps: Download your complete and correct algorithms (bisect.m, my Newton.m, and secant.m) from MGHW5 and save it to your own computer in a folder called Root Finding. Do not change the code in any of these three files! Open a new (driver) script m-file to complete the problems on this homework assignment. Call the functions you wrote. If you need to compute something like error (which is not an output of the algorithms), don't change the algorithms. Get the outputs and then manipulate them in your driver script. In conjunction with your driver script, refer to your handwritten notes about the algorithms to answer the "math" parts of the questions. 72 2. This problem will be completed in class on Monday 2/22. The function f(x) = (x-3) has one root, r* = 3. Starting with an initial guess x1 = 2, Newton's method generates the following sequence of approximations to r*. In error 12.0000 2 2.5000 3 2.7500 4 2.8750 5 2.9375 (a) (1 point) Fill in the error column of the table. Use a driver script to generate the data! (b) (1 point) Determine the order of convergence a associated to this test problem. Show your work to get the final computation. Continue to use the driver script! (e) (1 point) What facts about f(x) let you predict the convergence rate for this instance of Newton's method (without knowing the data in the table above)? X Bisection Method 9 solutions submitted (max: 10) | View my solutions Problem Summary Implement the bisection method as a function: function [p, n] = bisect(f, a, b, tol) We seek a root of the anonymous function f in the interval (a, b The function should retum an approximation p that is within a user input tol of the actual root as well as the number of iterations n it took to converge. As a class convention, we will take p to be the midpoint of the first interval smaller than tol As a class convention, we will count the first bisection as the midpoint of the supplied interval [a, b]. You do not need to worry about the exceptional case when a bisection lands exactly on a root. (You can if you want to, but you may assume this does not occur.) Debugging tips: If you are receiving an error message Unrecognized function or variable 'p' along with other errors and no test passed, check your stopping criteria. If you use the incorrect stopping criteria, your code will go into an infinite loop on one of the tests and never finish (so no outputs will be defined, hence the error message). There may be other problems, but this is most likely the cause. If test 1 is your only correct test, you are actually very close to correct code! It is likely that you stopped when the interval was shorter than tol, however, your value of p was not the midpoint of this interval. If you correct this, it is likely that this will provide passing results on all tests if you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. The first bisection (n=1) counts as the midpoint of the first interval . X Bisection Method 10 solutions submitted (max 10) | View my solutions Solution Details Test Results Solution 10: 5 of 9 tests passed Submitted less than a minute ago ID 59337209 Size: 103 1 function (p.n] - bisect(f, a, b, tol) 2 Xinput f, anonymous function for which we'd like to find a root 3 Xinputs a,b left and right ends for which f(a) f(b) 9 - P 10 else 11 b =D 12 end 13 pprev = P: 14 P- (a+b)/2 15 n-3; 16 while abs(pprev->-tol 17 if f(a) f(p) > 18 a- Di 19 else 20 b-pi 21 end 22 pprev - Pi 23 p = (a+b)/2; 24 n - n+1; 25 end 26 27 end Newton's Method 10 solutions submitted (max: 10) | View my solutions Problem Summary Implement Newton's method as a function function [P,n] = myNewton(f,fprime,xe,tol) We seek a root of the anonymous function f given an initial guess xo. We input f and its derivative fprime. We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p. Also output the number of iterations n it took to reach p As a class convention, we say that the initial guess counts as 1 iteration So, in a sense, n=2 would mean we took one step of Newton's method. Debugging tips If test 3 is the only test passed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other. if tests 1 and 7 are the only tests failed, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration . If your code failed to complete, with this message. Your code could not run to completion, possibly due to an out-of-memory condition. Common causes are either loading large files or a missing ";" from the end of a command.If the problem persists, contact the instructor, it is possible that you are not using the initial condition xo to start iterating in addition to the suggestion made by Matiad of using If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. We say that the initial guess is n = 1. So, in a sense n=2 would mean we took one step of Newton's method . Best Solution My Solutions Test Results Solution 9: 7 of 8 tests passed Submitted on 19 Feb 2021 at 23:44 | ID. 58075754 Size: 67 1 function [P,n] = myNewton(f,fprime ,xe,tol) 2 Xinput f, anonymous function for root finding problem 3 %input fprime, anonlymous function, the derivative of f 4 Linput xe, an initial guess 5 %input tol, a tolerance (method will stop when successive iterates are within 1 6 Zoutput p, a root f(p) = 7 Zoutput n, the number of iterations to reach p 8 n-1; 9 P = 99; 10 while(abs (P-XO)>-tol) p=0; 12 n=n+1; 13 b=(xe*fprime(xe))-f(xe); 14 x =(roots([fprime(x),-b])); 15 end 16 P=x0; 17 end 11 18 Secant method 7 solutions submitted (max 10) | View my solutions Problem Summary Implement the secant method as a function function [p, n] = secant(f,x0, x1, tol) We seek a root of the anonymous function f given initial guesses x@ and X1. We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p and the number of iterations n it took to get there. As a class convention, we count the two initial guesses as iterations. So, n= 3 is a single implementation of the secant method formula Debugging tips If test 3 is the only test failed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration If test 6 is the only test falled, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other . If tests 1-3 passed but tests 4-6 failed, it is possible that you are not using the initial conditions x0 and x1 to start iterating If you number of iterations is off by one, try chaning your intialization of n and/or the location of when you update n in the loop. We count the two initial guesses as iterations. So, n=3 is a single implementation of the secant method formula. Best Solution My Solutions Test Results Solution 7: All tests passed Submitted on 19 Feb 2021 at 17:10 | ID: 58016624 | Size: 73 1 function [2,n] = secant(f,xe, x1, tol) 2 %input f, root finding function 3 %inputs xe, x1, initial guesses 4 %input tol, a tolerance (stop once successive iterates are within tol of each 5 %ouptput p, a root f(p) = 0 6 %output n, the number of iterations to reach p 7 n=2; 8 er=1/tol; 9 while er>=tol 10 n=n+1; 11 p2=x1-(f(x1)*(x1-x))/(F(x1)-f(xe)); 12 er-abs (p2-x1); 13 x0=1; 14 x1=p2; 15 end 16 p-p2; 17 end 18 19 2e