mu123 maths
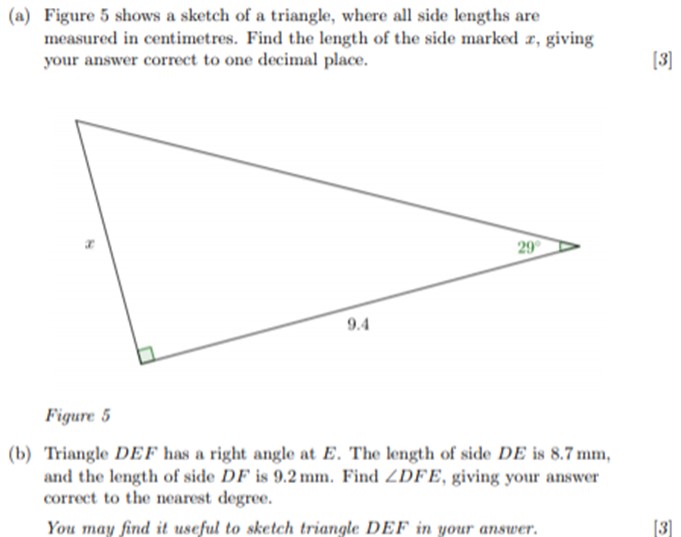
(d) (i) Convert 240 to radians, leaving your answer in terms of n. (ii) Use your answer from part (d) (i) to find the area of a sector of a circle of radius 5.3 centimetres and angle 24, giving your answer correct to two significant figures. Question 5 - 11 marks This question is based on your work on MU123 up to and including Unit 12. You should use trigonometry, not scale drawings, to find your answers. Melissa is testing the strength of radio signal she gets depending on how close she is to two Digital Audio Broadcasting (DAB) radio transmitters in the Lothians region of Scotland. One transmitter is at Athelstaneford in East Lothian. The other is the Braid Hills transmitter in Edinburgh. The two transmitters stand 26.8 km apart (in a straight line). Starting from the Athelstaneford transmitter, Melissa travels in a straight line for 11.9 km and stops. Her direction of travel is not directly towards the Braid Hills transmitter, but gets her closer to it. From her new position, she can see both transmitters. The angle formed between her (straight) lines of sight to the two transmitters is 1020. (a) Sketch a diagram of the situation, showing the points A for the position of the Athelstaneford transmitter, B for the position of the Braid Hills transmitter and M for the current position of Melissa. Mark in the angle and the lengths (in kilometres) that you are given. Join the three points with line segments to make the triangle ABM. (b) Melissa would like to calculate the distance between her current position and the Braid Hills transmitter. She realises that in triangle ABM she has two side lengths and an angle. She mistakenly concludes that she can solve her problem with a single direct application of the Cosine Rule, like in Example 9 in Subsection 2.2 of Unit 12. Explain, as if directly to Melissa, why she can't use the Cosine Rule directly in this way to solve her problem. (c) (i) Use the Sine Rule to find the angle at B. Give your answer correct to the nearest degree.(a) Figure 5 shows a sketch of a triangle, where all side lengths are measured in centimetres. Find the length of the side marked z, giving your answer correct to one decimal place. [3] 29% 9.4 Figure 5 (b) Triangle DEF has a right angle at E. The length of side DE is 8.7 mm, and the length of side DF is 9.2 mm. Find ZDFE, giving your answer correct to the nearest degree. You may find it useful to sketch triangle DEF in your answer. (31(c) (i) Figure 6 shows the triangle ABC, with all side lengths measured in centimetres. Find ZABC, giving your answer correct to the nearest degree. 17.1 14.4 B 3.2 Figure 6 (ii) Find the area of triangle ABC in Figure 6, giving your answer correct to the nearest square centimetre.(ii) Use your answer to part (c) (i) to find the angle at A. Give your answer correct to the nearest degree. (iii) Use the Cosine Rule and your answer to part (c) (ii) to find the distance between Melissa and the Braid Hills transmitter. Give your answer correct to two significant figures