MUST BE DONE IN C++

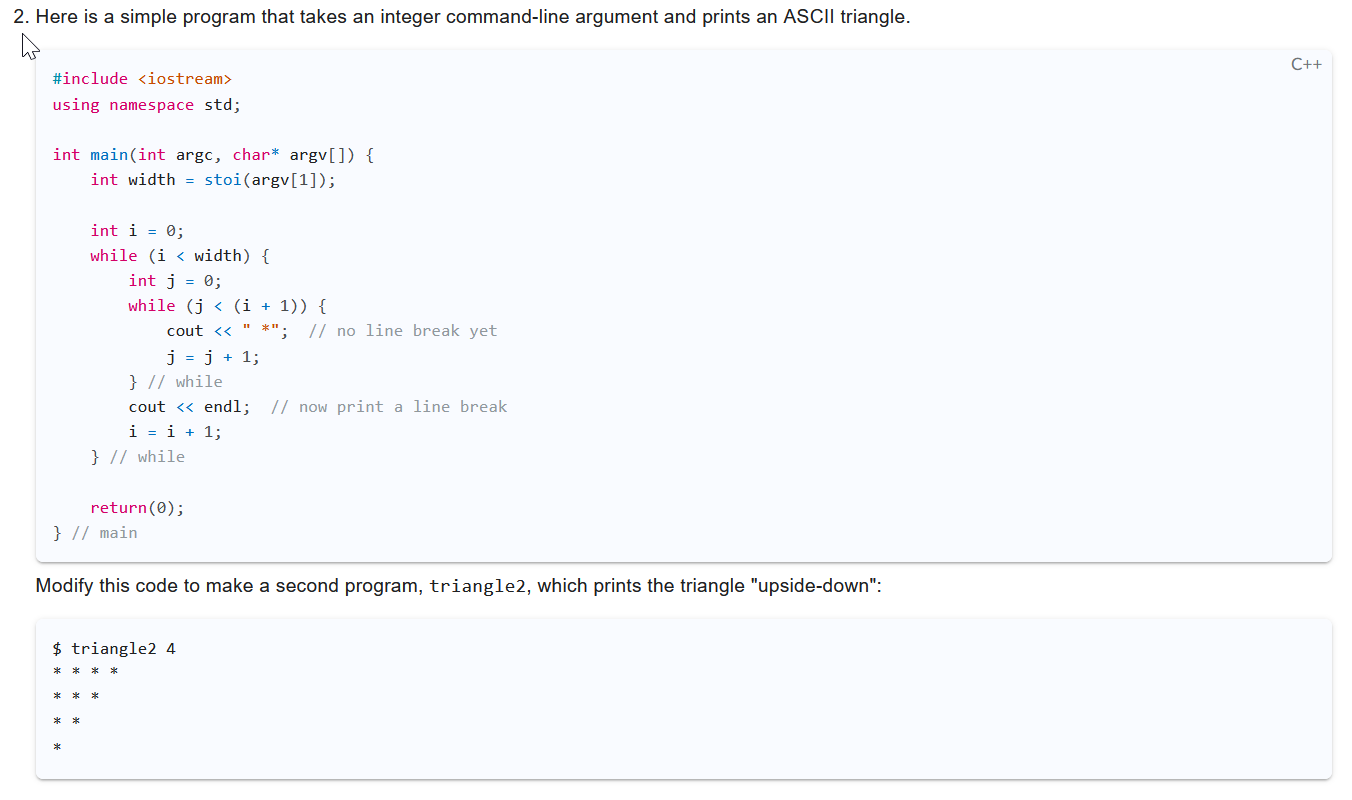
1. Write a program, nearestpow, which takes a command-line integer argument, n, and returns the largest integer less than or equal to n that is also a power of 2. For example: $ nearestpow 1 1 $ nearestpow 18 16 $ nearestpow 64 64 $ nearestpow 63 32 $ nearestpow 255 128 Here is a simple program that takes an integer command-line argument and prints an ASCII triangle. 3. The ratio of a circle's circumference to its diameter, 3.14159265, is an essential element of many formulae in engineering, physics, and mathematics. It is als o an irrational number, meaning that its decimal expansion is infinite and (unlike, say, 1/0.33333...) does not repeat. Still, there are a number of ways to calculate ap proximate values of , as precisely as one nee ds. A particularly simple (though very slow to converge) method is to use the infinite series sum =1434+5474+94114+ Although this method uses only simple arithmetic operations and calculates an approximation at any degree of accuracy, it is also very slow: even 6 di gits of accuracy (3.1415923) requires around 10 million terms of the series, and a 7 th digit needs 20 million! Your Job: Write a program, pi approx, which takes a single inte ger, n, as a command-line argument. The program should calculate an ap proximate value of with the first n terms of this infinite series and print the result. $ piapprox 1 approximation: 4 (target =3.1415926535897931) $ piapprox 6 approximation: 2.9760461760461765 (target =3.1415926535897931 ) $ piapprox 100 approximation: 3.1315929035585537 (target =3.1415926535897931 ) $ piapprox 10000 approximation: 3.1414926535900345 (target =3.1415926535897931 ) $ piapprox 1000000 approximation: 3.1415916535897743 (target =3.1415926535897931 ) $ piapprox 1000000000 approximation: 3.1415926525880504 (target =3.1415926535897931 ) $ piapprox 1500000000 approximation: 3.1415926532692002 (target =3.1415926535897931 ) NOTE \#1: If you'd like to add the "target" approximation that I have in the examples, here is how I did it in my code, using the acos () function from the cmath library and a call to set precision() that forces 16 digits of accuracy in the printout: NOTE \#2: You probably won't be able to use your program with a large enough argument to reach 16 digits of accuracy. Above 1.5 billion terms, the limits of integer and floating-point precision will likely lead to overflow errors. 4. Ever wonder how something like a pocket calculator from 40 years ago can compute something like a square root so quickly? The secret is that many of the basic mathematical functions have highly effective techniques for getting accurate approxi mations quickly. For example, square roots can be calculated with a 338 year old method developed by Isaac Newton. Here's the idea: you first guess what the s quare root might be, then see how close your guess is. You can use this information to make another guess (as a refinement of the previous one) and continue gues sing until you have found the square root (or a close approximation). More precisely, suppose x is the number we want the square root of and sqx is our current guess. Then we can improve this by using as our next guess sqX2.0sqX+sqXx Even starting with see mingly silly initial "guess" values for sqX, this method can be used to find an answer remarkably quickly. For example, 921.0+1.0925.0+5.0923.4+3.4923.02353+3.0235393.000092 or even: 92100.0+10009250.9+6099225.53841+26.88119212.94541+1201561926.820319+6.920319924.069953+4.009535923.14064+3400493.00325 Your job: Write a program, sqrt that takes a single floating-point argument, x. The program should compute an approximation of x by running Newton's method 10 times, using whatever initial "guess" value you'd like. If run with a negative-valued argument, or with no argument, the program should print an error message. Examples: $ sqrt 9 3 $ sqrt 15 3.872983346207417 $ sqrt 256 16 $ sqrt 256.1 16.603124694883809 $ sqrt -1 Square roots of negative numbers are not defined. $ sqrt USAGE : sqrt x NOTE: Do not us e the cmath function sqrt in your solution (nor any other cmath function). If you want to add it as a debugging check on your work, that's fine, but the solution itself must be done using the method above. Turn in Turn in copies of your four source code files: - nearestpow.cpp - triangle2.cpp - piapprox.cpp - sqrt.cpp