**** MUST be in Python Language

Recursive Functions

a) Binary Tree. Write a function in file p1.py with signature binary_tree(length, depth) that draws a binary tree figure like that from Figure 1 using the turtle module. The figure produced is similar to the example from the textbook with a significant difference that you will notice immediately: the left branches align on a right(60) angle from the vertical and the right branches all align on a left(60) angle from the vertical.

The binary tree drawing must look like that from Figure 1, except the dots are NOT required:

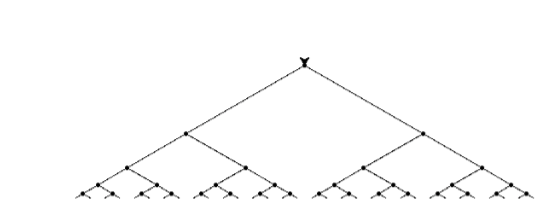
Figure 1. Binary tree produced by calling binary_tree(160, 5), with dots shown at starting points for clarification.

Include a screenshot of the figure drawn by the call binary_tree(160, 6).

To get credit for part a):

do not change the function signature,

do NOT draw the black dots,

the screenshot must be of the figure drawn by the call binary_tree(160, 6).

b) Efficient Power.

Consider the power(x,n) function, with x any number, and n a non-negative integer, that computes xn. Since we love recursion we may consider this trivial implementation of power:

def power_linear(x, n): if n == 0:

return 1 return x * power_linear(x, n-1)

The problem with this function is that it has a runtime proportional to n; we say its runtime complexity is linear in n and we write that as O(n). E.g. if n == 31, this function does 31 multiplications, in 31 recursive calls.

We quickly realize that we can make power work a lot faster by using a smarter dive-and-conquer approach. For example, if n == 28, we can compute power(x, 28) as follows:

power(x, 28) = power(x, 14)2 power(x, 14) = power(x, 7)2

power(x, 7) = x * power(x, 3)2 power(x, 3) = x * power(x, 1)2

power(x, 1) = x * power(x, 0) power(x, 0) = 1

To do for part b):

Write a new version of the power function that uses this second approach (in file p1.py). Write the

contract for the function in its docstring: what it does and the preconditions.

Write a function called test_power() that uses the testif module/function to test the power() function for the base case and some other cases. Compare with ** the operator.

Part c) Memoized Slice Sums. For this problem, first you need to write a recursive function slice_sum(lst, begin, end) that computes recursively the sum lst[begin] + lst[begin+1] + lst[begin+2] + ...+lst[begin+end-1]. Parameter lst is a list object or a tuple. This function returns exactly the same value as expression sum(lst[begin:end]).

The base case deals with an empty slice and the recursive case adds lst[begin] to the sum_slice() on the remainder of the list.

This function must NOT use slice notation (e.g. lst[i:j]) or no credit is given. Write the function contract (including preconditions related to valid parameter range) in its docstring. The function should be allowed to throw IndexError if the index parameters are invalid.

Write a unit test function test_slice_sum() that uses testif() to test function slice_sum() for interesting cases, including the base case.

Second, after the recursive version of slice_sum() function works correctly, write a second version of this function that uses memoization to optimize it. Call the memoized function slice_sum_m. This function caches function values returned for various values of parameters begin and end..

We can make the simplifying assumptions that over the execution time of the program the function slice_sum_m is called always with the same object referenced by parameter lst and that object never changes. (Otherwise it would make no sense to cache results!)

Write a unit test function test_slice_m() that uses testif() to test function slice_sum_m() for interesting cases, including the base case.

So, for part c) write in file p2.py functions sum_slice(), test_slice_sum(), sum_slice_m(), and test_slice_sum_m().