My current code:

f1=@(x)(exp(-x.^2));%f1

datx=(-3:1:3)';%datapoints

daty=f1(datx);

x=(-3:.1:3)';%interpolation points

P1=Lagrange_poly(x,datx,daty)%Test P1

f2=@(x)(1./(1+x.^2));%f2

daty=f2(datx);

P2=Lagrange_poly(x,datx,daty)%Test P2

datx=-3:.5:3;%other data points

daty=f1(datx);

P3=Lagrange_poly(x,datx,daty)%Test P3

daty=f2(datx);

P4=Lagrange_poly(x,datx,daty)

%PLOT

fplot(f1,[-3,3]);

hold on

scatter(datx,f1(datx),'*')

scatter(x,P1,'d')

scatter(x,P3,'filled')

legend('f1(x)','data points','P1','P3')

title('for f1')

figure

fplot(f2,[-3,3],'r');

hold on

scatter(datx,f2(datx),'*')

scatter(x,P2,'d')

scatter(x,P4,'filled')

legend('f2(x)','data points','P2','P4')

title('for f2')

function y=Lagrange_poly(x,datx,daty)

m=length(datx);

ybar=zeros(size(x));

for k=1:numel(x)

result=0;

for i=1:m

term=daty(i);

for j=1:m

if i~=j

term=term*(x(k)-datx(j))/(datx(i)-datx(j));

end

end

result=result+term;

end

ybar(k)=result;

end

y=ybar;

end

Submission feedback:

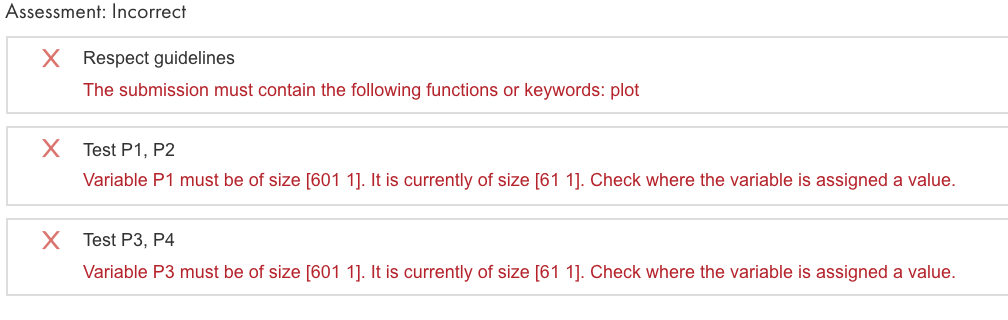Please edit my code to fullfill submission requirements or completely write a new one if wrong. Thanks.

1. Write a MATLAB function, called Lagrange_poly that inputs a set of data points (x, y) (datx, daty) a set x of numbers at which to interpolate, and outputs the polynomial interpolant, y, evaluated at x using Lagrange polynomial interpolation. Your function header should look something like: function y = Lagrange-poly(x, datx, daty) (a) Use the code you developed to interpolate the functions i, fi (z)= e-z? ii. f2(x)= using the data points datx--3 : 1 :3. Interpolate at the points x=-3: 0.01 : 3. Call Pl the La- grange interpolant of fi, and P2 the Lagrange interpolant of f2. Repeat the experiment except using the data dat x1-3: 05: 3. Call in that case P3 and P4 the new interpolants. Compare r answer for this problem to what you got previously. For each interpolation problem, plot on the same graph the function, the two interpolants, and the data set (use the function scatter). Comment the results in your matlab script using %