My StackADT class

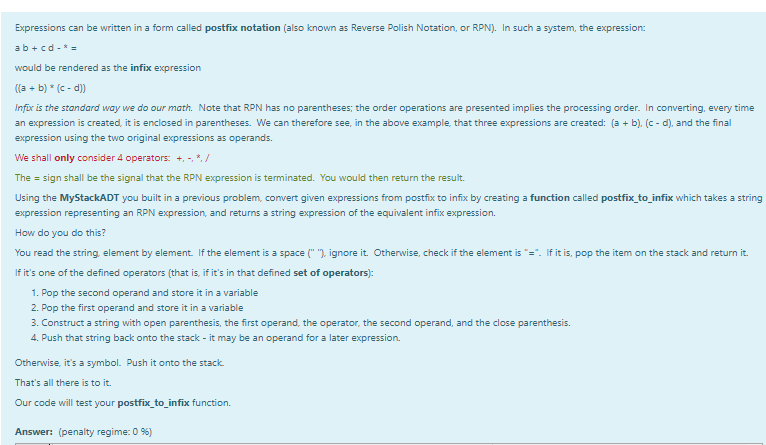
class MyStackADT(object): s = None def push(self,new_item): if(self.s == None): self.s = deque([new_item]) else: self.s.appendleft(new_item) def pop(self): if(self.s == None): return None else: return self.s.popleft() def is_empty(self): if(self.s == None) or len(self.s) == 0: return True return False def peek(self): if (self.s != None): first = deecopy(self.s[len(self.s)-1]) return first else: return None def __str__(self): info = "" for i in self.s: info = info + str(i) + " " return info 

Expressions can be written in a form called postfix notation (also known as Reverse Polish Notation, or RPN). In such a system, the expression: ab + cd. would be rendered as the infix expression [(a + b) * (c- d)) Infix is the standard way we do our math. Note that RPN has no parentheses; the order operations are presented implies the processing order. In converting, every time an expression is created, it is enclosed in parentheses. We can therefore see, in the above example, that three expressions are created: (a + b). (c-d), and the final expression using the two original expressions as operands. We shall only consider 4 operators: +.- */ The = sign shall be the signal that the RPN expression is terminated. You would then return the result. Using the MyStackADT you built in a previous problem, convert given expressions from postfix to infix by creating a function called postfix_to_infix which takes a string expression representing an RPN expression and returns a string expression of the equivalent infix expression. How do you do this? You read the string, element by element. If the element is a space (" "), ignore it. Otherwise, check if the element is "=". If it is pop the item on the stack and return it. If it's one of the defined operators (that is, if it's in that defined set of operators): 1. Pop the second operand and store it in a variable 2. Pop the first operand and store it in a variable 3. Construct a string with open parenthesis, the first operand, the operator, the second operand, and the close parenthesis. 4. Push that string back onto the stack - it may be an operand for a later expression Otherwise, it's a symbol. Push it onto the stack That's all there is to it Our code will test your postfix_to_infix function. Answer: (penalty regime: 095)