My today's work.
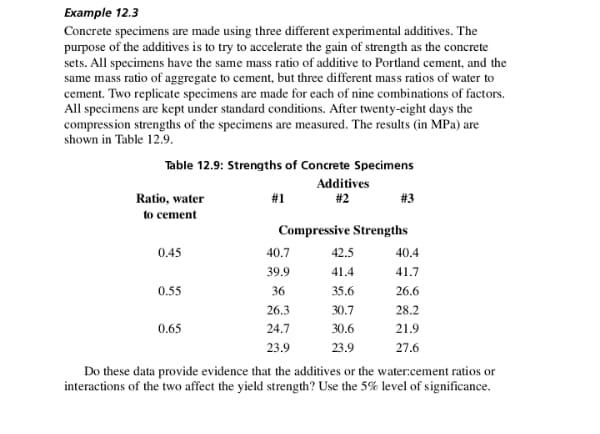
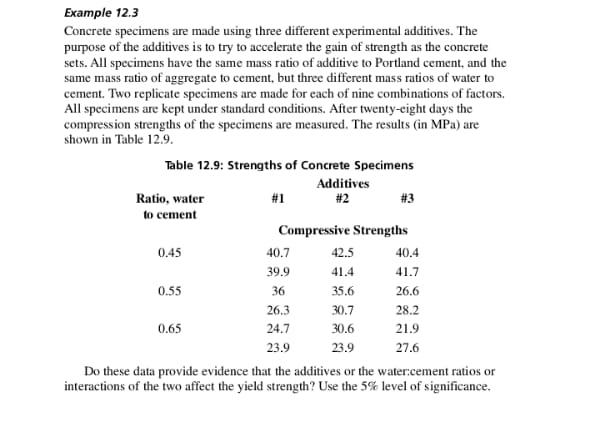
Example 3.3 Consider the sample consisting of the following nine results : 23, 7.2, 3.7, 4.6, 5.0, 7.0, 3.7. 4.9, 4.2. a) Find the median of this set of results by two different methods. b) Find the lower quartile. c) Find the upper quartile. d) Estimate the probability that an item, from the population from which this sample came, would be less than 4.9. e) Estimate the probability that an item from that population would be less than 3.7.Example 5.10 A boiler containing eight welds is manufactured in a small shop. When the boiler is completed, each weld is checked by an inspector. If more than one weld is defective on a single boiler, the person who made that boiler is reported to the foreman. a) If 9.0% of all welds made by Joe Smith are defective, what percentage of all boilers made by him will have more than one defective weld? b) Over a long period of time how many times will Joe Smith be reported to the foreman for each 15 boilers he makes? c) If Joe makes 15 boilers in a shift, what is the probability that he will be reported for more than two of these 15 boilers?Example 7.4 The strengths of individual bars made by a certain manufacturing process are ap- proximately normally distributed with mean 28.4 and standard deviation 2.95 (in appropriate units). To ensure safety, a customer requires at least 95% of the bars to be stronger than 24.0. a) Do the bars meet the specification? b) By improved manufacturing techniques the manufacturer can make the bars more uniform (that is, decrease the standard deviation). What value of the standard deviation will just meet the specification if the mean stays the same?Example 7.3 In another city 2500 electric lamps are installed for street lighting. The lamps come from a different manufacturer and have a mean burning life of 1050 hours. We know from past experience that the distribution of burning lives approximates a normal distribution. The 250th lamp fails after 819 hours. Approximately what is the stan- dard deviation of burning lives for this set of lamps?Example 9.8 Two methods of determining the nickel content of steel are compared using four determinations by each method. The results are: For method 1: x, = 3.2850, s, = 0.00774 (from 3 degrees of freedom) For method 2: X, = 3.2580, $2 = 0.00960 (from 3 degrees of freedom) Assuming that the two estimates of variance are compatible, is the difference in means statistically significant at the 5% level of significance?Example 12.3 Concrete specimens are made using three different experimental additives. The purpose of the additives is to try to accelerate the gain of strength as the concrete sets. All specimens have the same mass ratio of additive to Portland cement, and the same mass ratio of aggregate to cement, but three different mass ratios of water to cement. Two replicate specimens are made for each of nine combinations of factors, All specimens are kept under standard conditions. After twenty-eight days the compression strengths of the specimens are measured. The results (in MPa) are shown in Table 12.9. Table 12.9: Strengths of Concrete Specimens Additives Ratio, water #1 #2 #3 to cement Compressive Strengths 0.45 40.7 42.5 40.4 39 9 41.4 41.7 0.55 36 35.6 26.6 26.3 30.7 28.2 0.65 24.7 30.6 21.9 23.9 23.9 27.6 Do these data provide evidence that the additives or the water:cement ratios or interactions of the two affect the yield strength? Use the 5% level of significance