need def region_montecarlo_volume(self, n=1000): and def region_montecarlo_difference(self, other, n=1000):

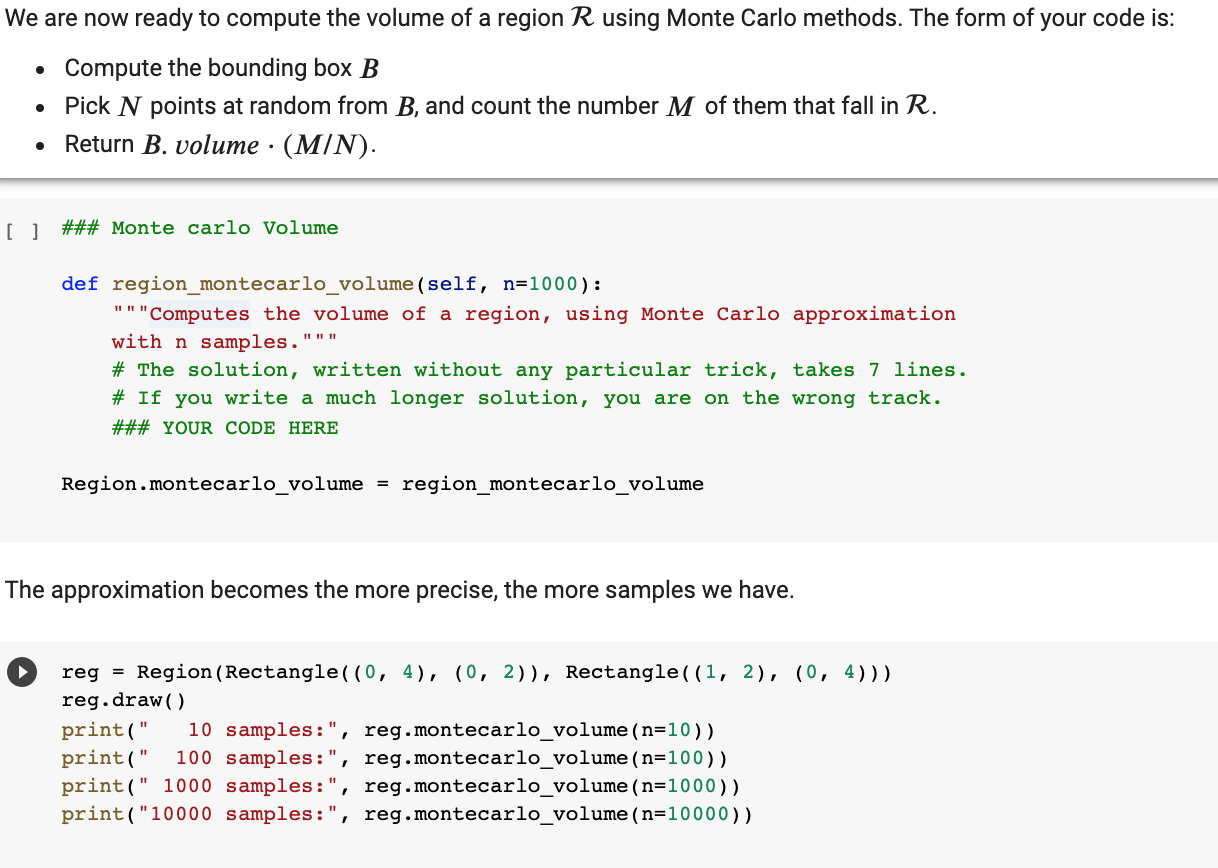
import string class Rectangle(object): def init__(self, *intervals, name=None): """A rectangle is initialized with a list, whose elements are either Interval, or a pair of numbers. It would be perhaps cleaner to accept only list of intervals, but specifying rectangles via a list of pairs, with each pair defining an interval, makes for a concise shorthand that will be useful in tests. Every rectangle has a name, used to depict it. If no name is provided, we invent a random one.""" self.intervals = [] for i in intervals: self.intervals.append(i if type(i) == Interval else Interval(*i)) # I want each rectangle to have a name. if name is None: self.name = "'.join( random.choices(string.ascii_letters + string.digits, k=8)) else: self.name = name def repr (self): "Function used to print a rectangle. s = "Rectangle " + self.name + ": " s += repr([(i.x0, i.xl) for i in self.intervals]) return S def clone (self, name=None): """Returns a clone of itself, with a given name. name or self.name + "" return Rectangle(*self.intervals, name=name) name = def _len_(self): "" "Returns the number of dimensions of the rectangle (not the length of the edges). This is used with _getitem__ below, to get the interval along a dimension. return len(self.intervals) 11 11 11 def getitem_(self, n): "" "Returns the interval along the n-th dimension" return self.intervals[n] def setitem_(self, n, i): """Sets the interval along the n-th dimension to be i""" self.intervals[n] = i @property def ndims (self): """Returns the number of dimensions of the interval.' return len(self.intervals) @property def volume (self): return np.prod([i.length for i in self.intervals]) We are now ready to compute the volume of a region R using Monte Carlo methods. The form of your code is: Compute the bounding box B Pick N points at random from B, and count the number M of them that fall in R. Return B. volume (M/N). [] ### Monte carlo Volume def region_montecarlo_volume (self, n=1000): '"Computes the volume of a region, using Monte Carlo approximation with n samples.""" # The solution, written without any particular trick, takes lines. # If you write a much longer solution, you are on the wrong track. ### YOUR CODE HERE Region.montecarlo_volume = region_montecarlo_volume The approximation becomes the more precise, the more samples we have. reg = Region (Rectangle( (0, 4), (0, 2)), Rectangle((1, 2), (0, 4))) reg.draw() print(" 10 samples:", reg.montecarlo_volume (n=10)) print(" 100 samples:", reg.montecarlo_volume (n=100)) print(" 1000 samples:", reg.montecarlo_volume (n=1000)) print("10000 samples:", reg.montecarlo_volume (n=10000)) # 10 points: Volume via Monte Carlo reg = Region (Rectangle((0, 1), (0, 4)), Rectangle((0, 4), (0, 1))) reg.draw() print(" 10 samples:", reg.montecarlo_volume (n=10)) print(" 100 samples:", reg.montecarlo_volume (n=100)) print(" 1000 samples:", reg.montecarlo_volume (n=1000)) print("10000 samples:", reg.montecarlo_volume (n=10000)) v = reg.montecarlo_volume(n=10000) assert 6.2