Need help in solving these problems. It would be a great help if you explain it with solutions. Thank you

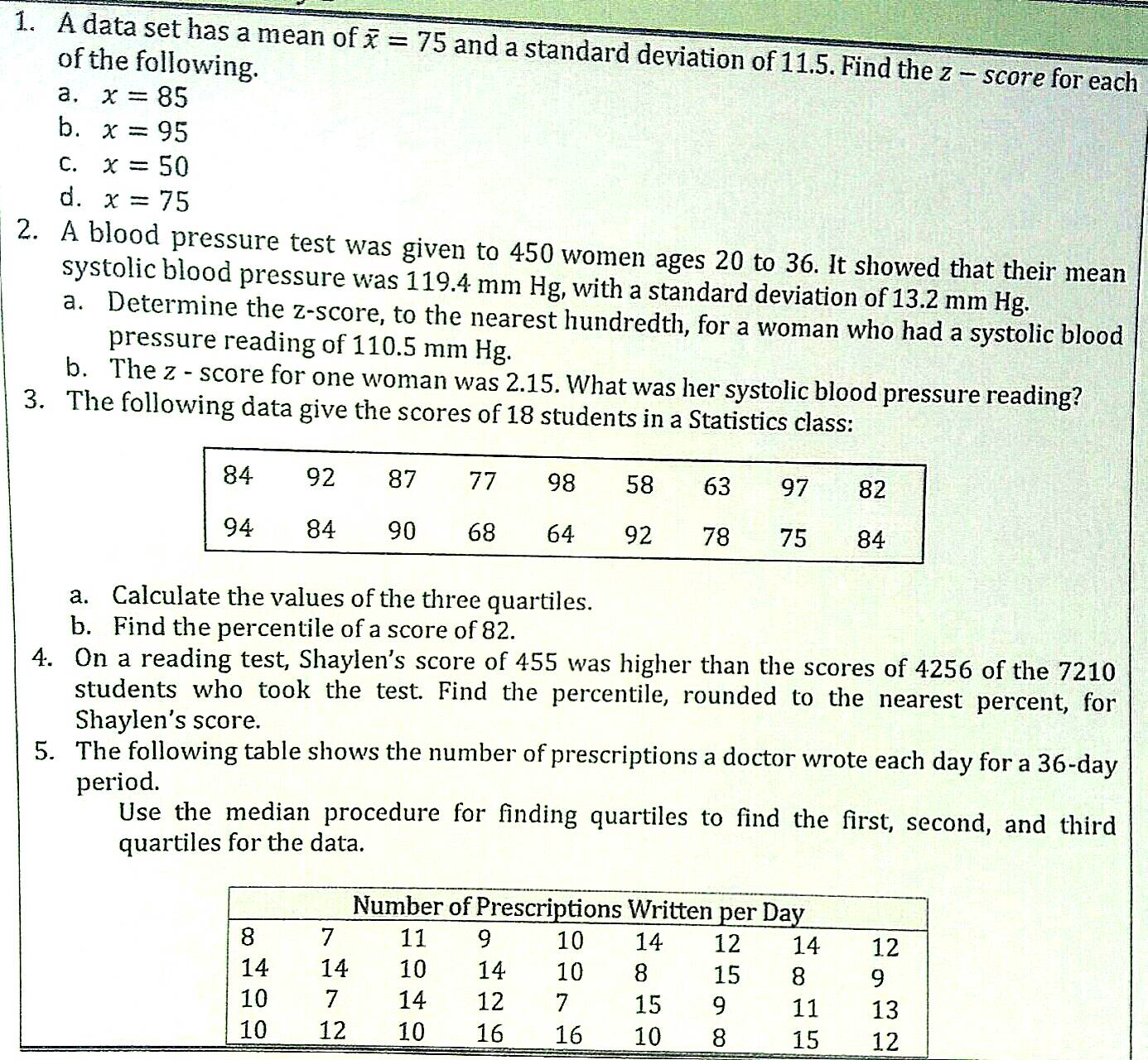
I. Identify whether the following statements is a descriptive or inferential statistics. 1. Last semester, the ages of students at a certain college ranged from 16 to 25 years old. 2. Based on the survey conducted by the National Statistics Office, it is estimated that 24% of unemployed people are women. 3. A survey says that 1 out of 10 Filipinos is a member of a fitness center. 4. A recent study showed that eating garlic can lower blood pressure. 5. After studying the effects of the gradual increase in dosage of a certain drug on cancer patients, a scientist concludes that the drug can arrest cancer cell growth at increased quantities in all cancer patients. II. Classify the following variables as qualitative or quantitative. If the variable is quantitative, identify if it is discrete or continuous. Then, identify further whether each variable is nominal, ordinal, interval, or ratio. 1. Room temperature 2. Color of cellular phone casing 3. Number of dining customers 4. Serial number of car motors 5. Flavor of ice cream 6. Height of mercury level in a barometer 7. Educational attainment of teachers III. Answer the following problems comprehensively. 1. Find the mean, the median, and the mode in each of the following list of data. a. 8, 3, 3, 17, 9, 22, 19 b. 11, 8, 2, 5, 17, 39, 52, 42 c. 101, 88, 74, 60, 12, 94, 74, 85 2. A professor grades students on 5 tests, a project, and a final examination. Each test counts as 10% of the course grade. The project counts as 20% of the course grade. The final examination counts as 30% of the course grade. Samantha has test scores of 70, 65, 82, 94, and 85. Samantha's project score is 92. Her final examination score is 80. Use the weighted mean formula to find Samantha's average for the course. Hint: The sum of all the weights is 100%. 3. A salesperson records the following daily expenditures during a 10-day trip. P185.34 P234.55, P211.86, P147.65, P205.60, P216.74, P1345.75, P184.16, P320.45, P88.12. In your opinion, does the mean or the median of the expenditures best represent the salesperson's average daily expenditure? Explain your reasoning 4. If exactly one number in a set of data is changed, will this necessarily change the mean of the set? Explain. 5. If exactly one number in a set of data is changed, will this necessarily change the median of the set? Explain. 6. If a set of data has a mode, then must the mode be one of the numbers in the set? Explain.of the following. 1. A data set has a mean of * = 75 and a standard deviation of 11.5. Find the z - score for each a. x = 85 b. x = 95 C. x = 50 d. x = 75 2. A blood pressure test was given to 450 women ages 20 to 36. It showed that their mean systolic blood pressure was 119.4 mm Hg, with a standard deviation of 13.2 mm Hg. a. Determine the z-score, to the nearest hundredth, for a woman who had a systolic blood pressure reading of 110.5 mm Hg. b. The z - score for one woman was 2.15. What was her systolic blood pressure reading? 3. The following data give the scores of 18 students in a Statistics class: 84 92 87 77 98 58 63 97 82 94 84 90 68 64 92 78 75 84 a. Calculate the values of the three quartiles. b. Find the percentile of a score of 82. 4. On a reading test, Shaylen's score of 455 was higher than the scores of 4256 of the 7210 students who took the test. Find the percentile, rounded to the nearest percent, for Shaylen's score. 5. The following table shows the number of prescriptions a doctor wrote each day for a 36-day period. Use the median procedure for finding quartiles to find the first, second, and third quartiles for the data. Number of Prescriptions Written per Day 8 7 11 9 10 14 12 14 12 14 14 10 14 10 8 15 8 9 10 7 14 12 7 15 9 11 13 10 12 10 16 16 10 8 15 12Find the range, the standard deviation, and the variance for the given samples. Round non- integer results to the nearest tenth. a. 1, 2, 5, 7, 8, 19, 22 b. 3, 4, 7, 11, 12, 12, 15, 16 c. 2.1, 3.0, 1.9, 1.5, 4.8 d. 5.2, 11.7, 19.1, 3.7, 8.2, 16.3 2. A mountain climber plans to buy some rope to use as a lifeline. Which of the following would be the better choice? Explain why you think your choice is the better choice. Rope A: Mean breaking strength: 500 lb; standard deviation of 100 lb Rope B: Mean breaking strength: 500 lb; standard deviation of 10 lb 3. Evaluate the accuracy of the following statement: When the mean of a data set is large, the standard deviation will be large. Explain