Need help on drawing rectangles in code and needs to pass given tests

Code needs to be written where it says "YOUR CODE HERE"

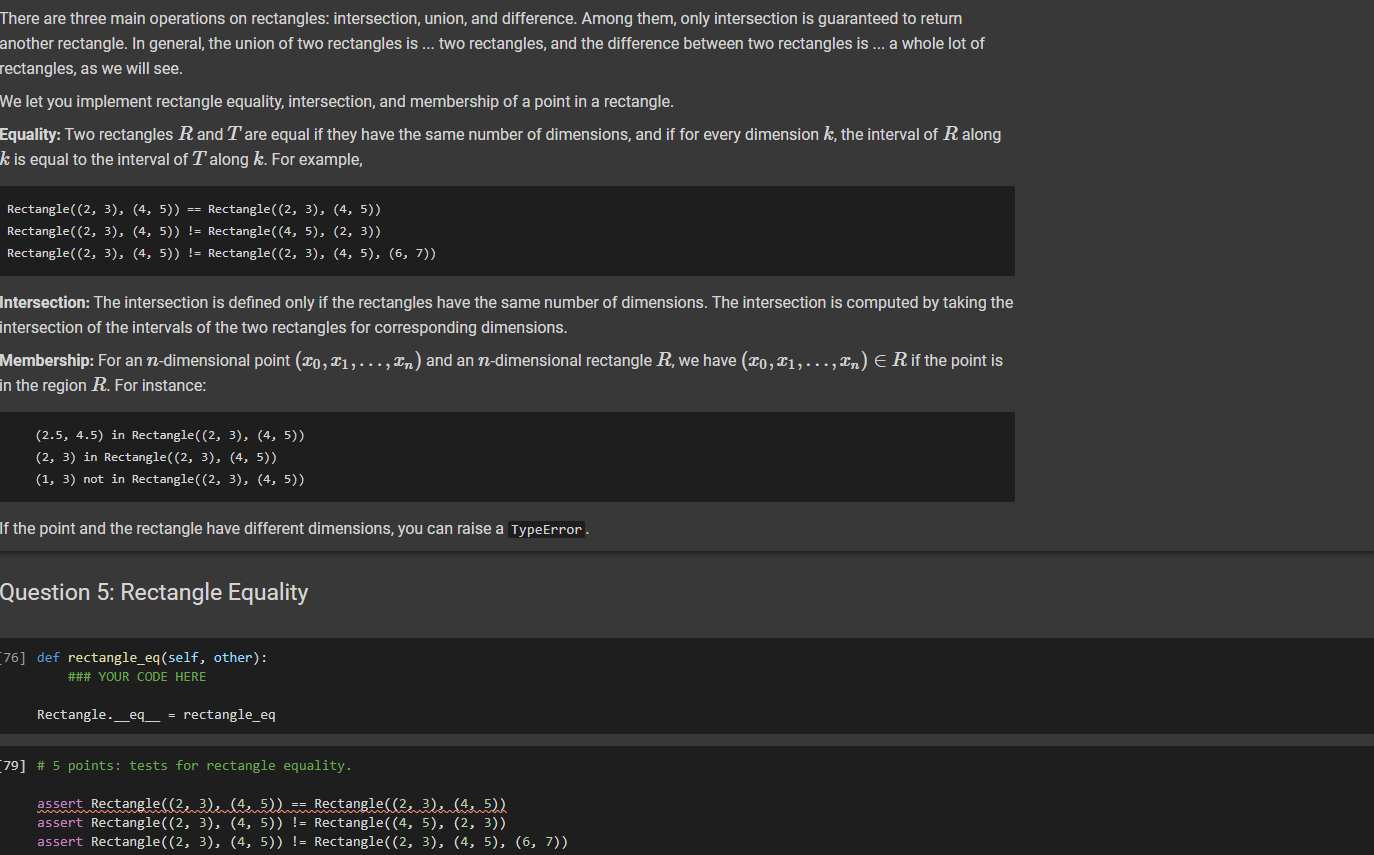
def rectangle_eq(self, other):

### YOUR CODE HERE

Rectangle.__eq__ = rectangle_eq

# 5 points: tests for rectangle equality.

assert Rectangle((2, 3), (4, 5)) == Rectangle((2, 3), (4, 5))

assert Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3))

assert Rectangle((2, 3), (4, 5)) != Rectangle((2, 3), (4, 5), (6, 7))

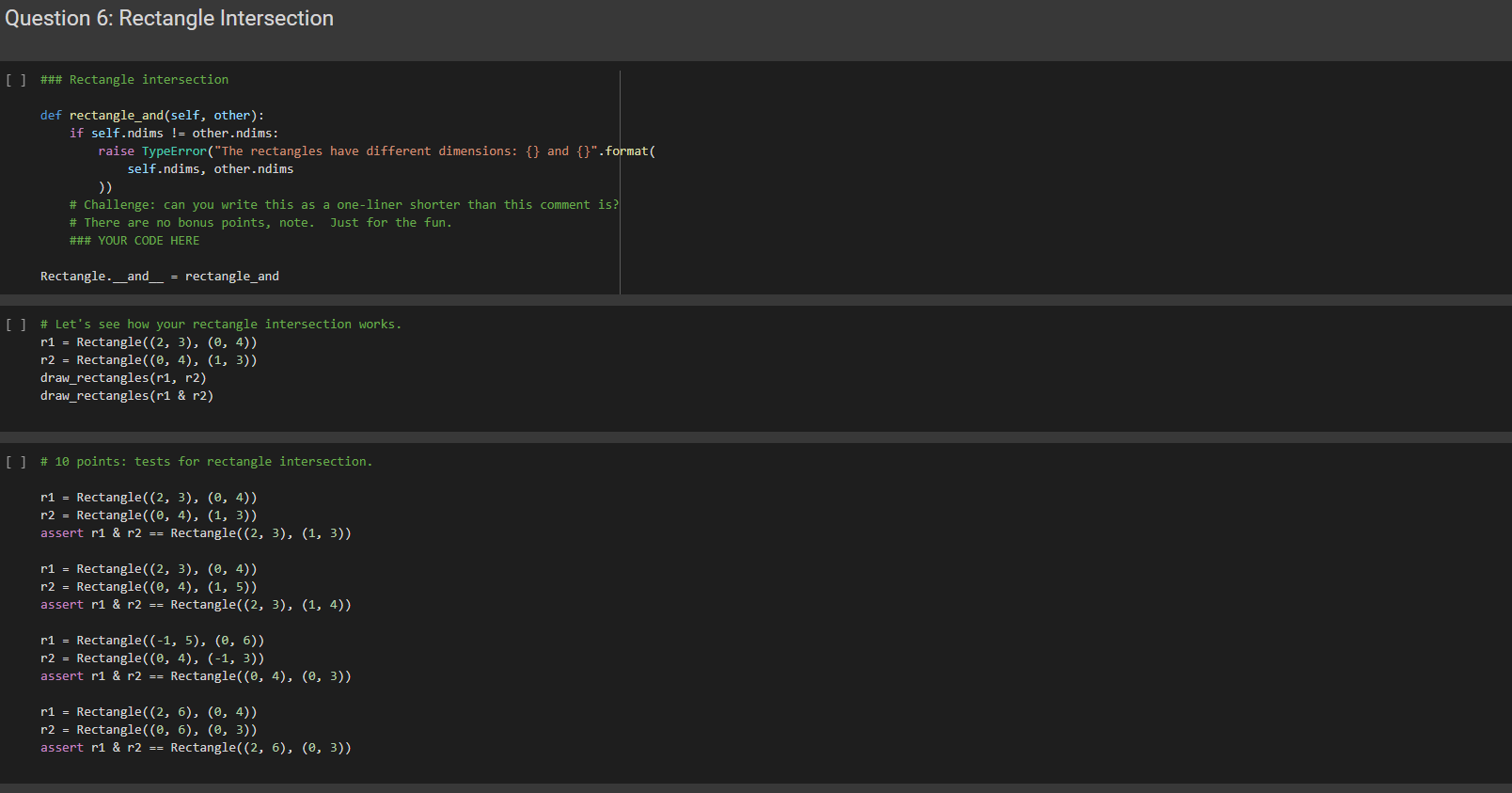
### Rectangle intersection

def rectangle_and(self, other):

if self.ndims != other.ndims:

raise TypeError("The rectangles have different dimensions: {} and {}".format(

self.ndims, other.ndims

))

# Challenge: can you write this as a one-liner shorter than this comment is?

# There are no bonus points, note. Just for the fun.

### YOUR CODE HERE

Rectangle.__and__ = rectangle_and

# 10 points: tests for rectangle intersection.

r1 = Rectangle((2, 3), (0, 4))

r2 = Rectangle((0, 4), (1, 3))

assert r1 & r2 == Rectangle((2, 3), (1, 3))

r1 = Rectangle((2, 3), (0, 4))

r2 = Rectangle((0, 4), (1, 5))

assert r1 & r2 == Rectangle((2, 3), (1, 4))

r1 = Rectangle((-1, 5), (0, 6))

r2 = Rectangle((0, 4), (-1, 3))

assert r1 & r2 == Rectangle((0, 4), (0, 3))

r1 = Rectangle((2, 6), (0, 4))

r2 = Rectangle((0, 6), (0, 3))

assert r1 & r2 == Rectangle((2, 6), (0, 3))

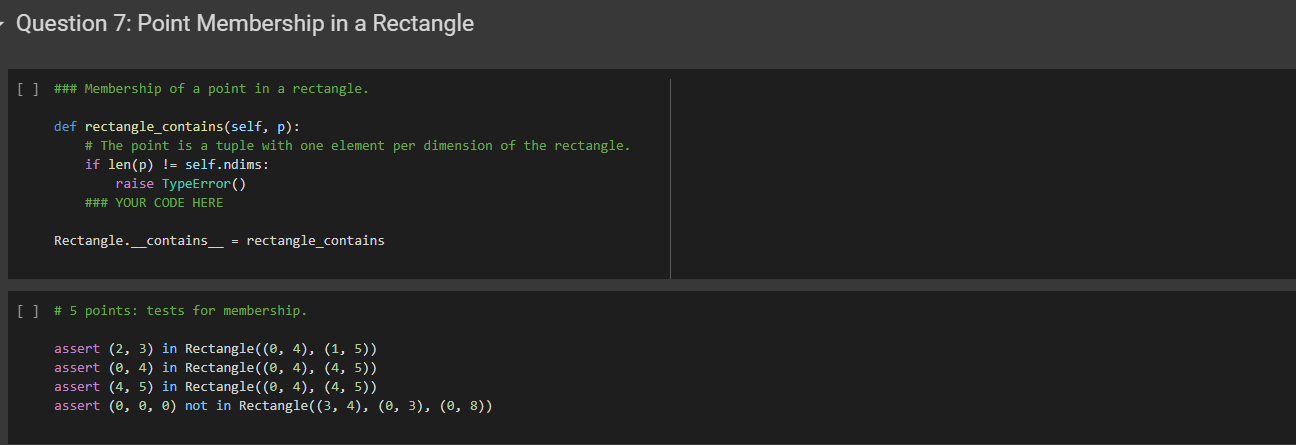
### Membership of a point in a rectangle.

def rectangle_contains(self, p):

# The point is a tuple with one element per dimension of the rectangle.

if len(p) != self.ndims:

raise TypeError()

### YOUR CODE HERE

Rectangle.__contains__ = rectangle_contains

# 5 points: tests for membership.

assert (2, 3) in Rectangle((0, 4), (1, 5))

assert (0, 4) in Rectangle((0, 4), (4, 5))

assert (4, 5) in Rectangle((0, 4), (4, 5))

assert (0, 0, 0) not in Rectangle((3, 4), (0, 3), (0, 8))

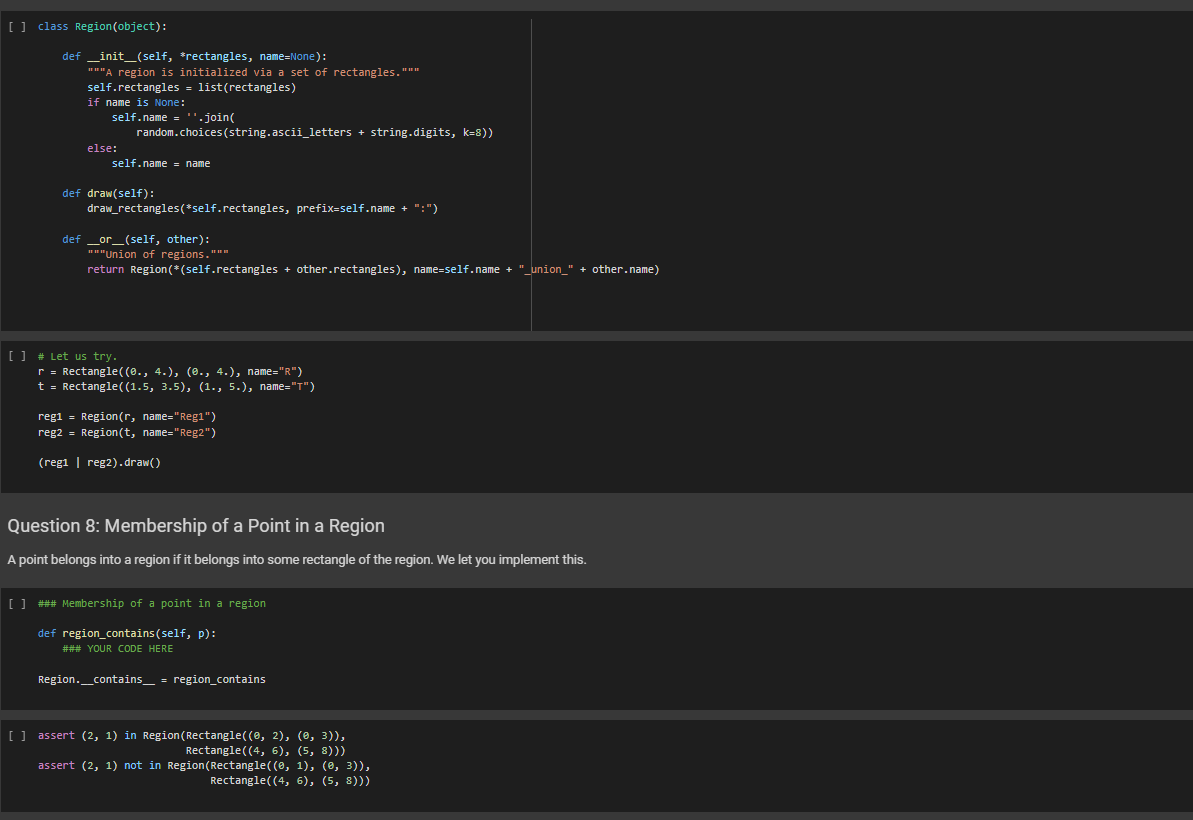
### Membership of a point in a region

def region_contains(self, p):

### YOUR CODE HERE

Region.__contains__ = region_contains

assert (2, 1) in Region(Rectangle((0, 2), (0, 3)),

Rectangle((4, 6), (5, 8)))

assert (2, 1) not in Region(Rectangle((0, 1), (0, 3)),

Rectangle((4, 6), (5, 8)))

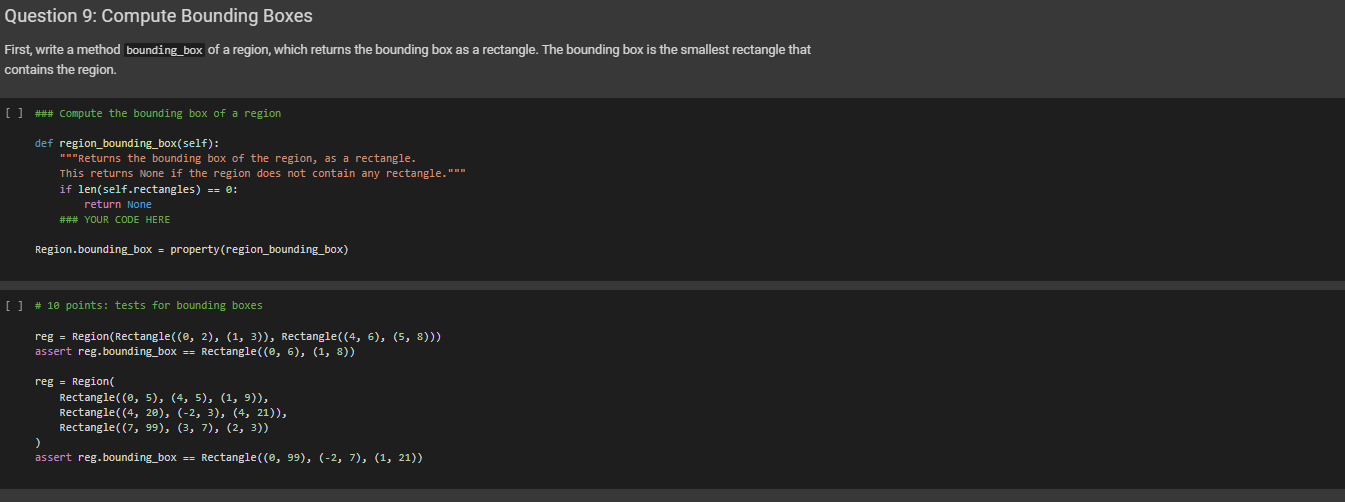
### Compute the bounding box of a region

def region_bounding_box(self):

"""Returns the bounding box of the region, as a rectangle.

This returns None if the region does not contain any rectangle."""

if len(self.rectangles) == 0:

return None

### YOUR CODE HERE

Region.bounding_box = property(region_bounding_box)

# 10 points: tests for bounding boxes

reg = Region(Rectangle((0, 2), (1, 3)), Rectangle((4, 6), (5, 8)))

assert reg.bounding_box == Rectangle((0, 6), (1, 8))

reg = Region(

Rectangle((0, 5), (4, 5), (1, 9)),

Rectangle((4, 20), (-2, 3), (4, 21)),

Rectangle((7, 99), (3, 7), (2, 3))

)

assert reg.bounding_box == Rectangle((0, 99), (-2, 7), (1, 21))

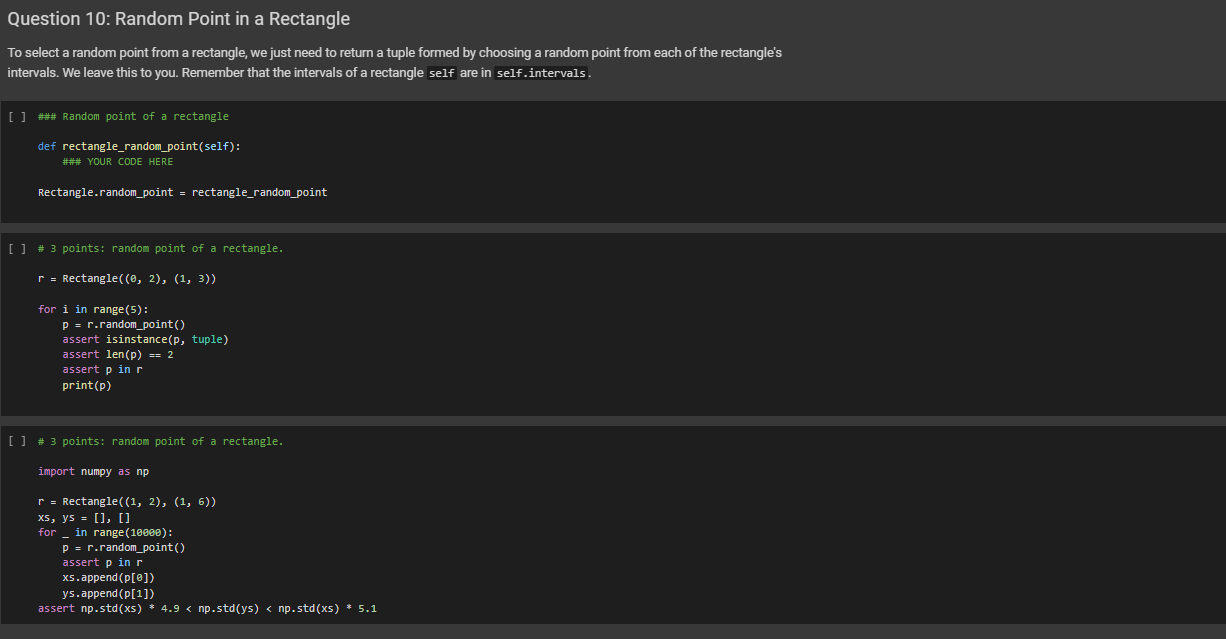
### Random point of a rectangle

def rectangle_random_point(self):

### YOUR CODE HERE

Rectangle.random_point = rectangle_random_point

# 3 points: random point of a rectangle.

r = Rectangle((0, 2), (1, 3))

for i in range(5):

p = r.random_point()

assert isinstance(p, tuple)

assert len(p) == 2

assert p in r

print(p)

# 3 points: random point of a rectangle.

import numpy as np

r = Rectangle((1, 2), (1, 6))

xs, ys = [], []

for _ in range(10000):

p = r.random_point()

assert p in r

xs.append(p[0])

ys.append(p[1])

assert np.std(xs) * 4.9

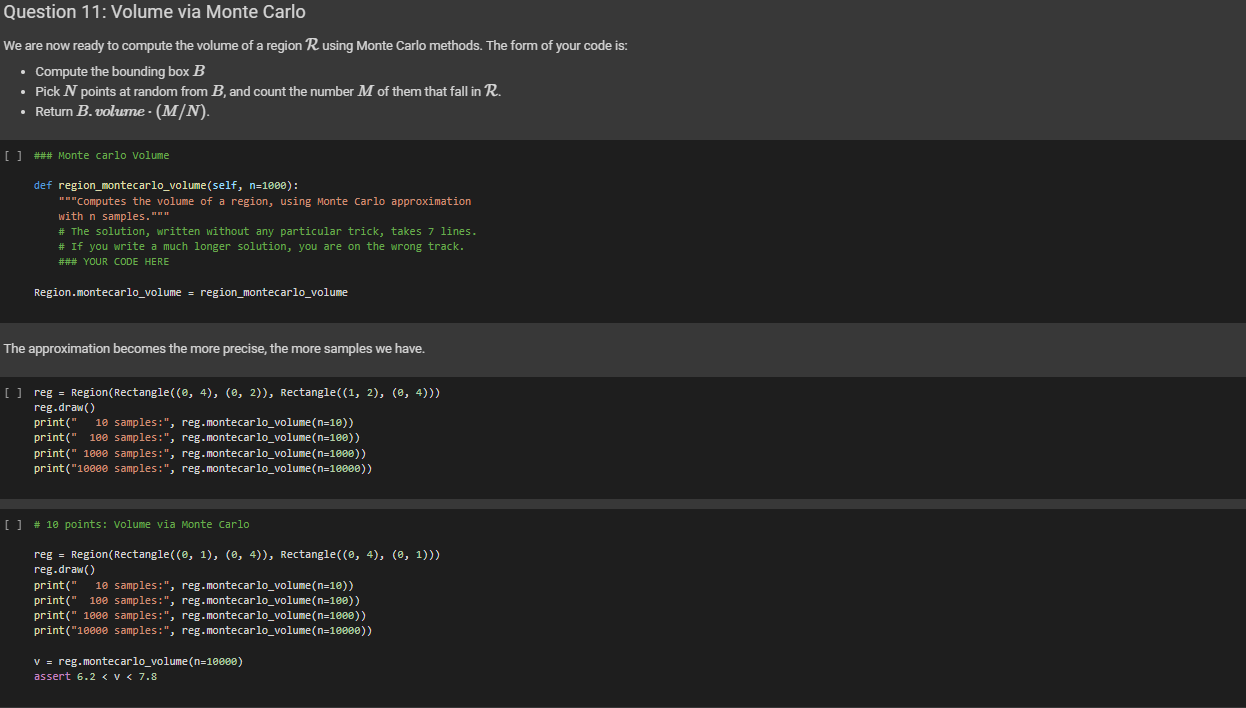
### Monte carlo Volume

def region_montecarlo_volume(self, n=1000):

"""Computes the volume of a region, using Monte Carlo approximation

with n samples."""

# The solution, written without any particular trick, takes 7 lines.

# If you write a much longer solution, you are on the wrong track.

### YOUR CODE HERE

Region.montecarlo_volume = region_montecarlo_volume

# 10 points: Volume via Monte Carlo

reg = Region(Rectangle((0, 1), (0, 4)), Rectangle((0, 4), (0, 1)))

reg.draw()

print(" 10 samples:", reg.montecarlo_volume(n=10))

print(" 100 samples:", reg.montecarlo_volume(n=100))

print(" 1000 samples:", reg.montecarlo_volume(n=1000))

print("10000 samples:", reg.montecarlo_volume(n=10000))

v = reg.montecarlo_volume(n=10000)

assert 6.2

### Monte Carlo difference and equality between regions

def region_montecarlo_difference(self, other, n=1000):

"""Checks whether a region self is different from a region other, using

a Monte Carlo method with n samples. It returns either a point p that

witnesses the difference of the regions, or None, if no such point is found."""

# This can be done without hurry in 6 lines of code.

### YOUR CODE HERE

Region.montecarlo_difference = region_montecarlo_difference

def region_montecarlo_equality(self, other, n=1000):

return self.montecarlo_difference(other, n=n) is None

Region.montecarlo_equality = region_montecarlo_equality

# 10 points: Equality of regions via Monte Carlo.

reg1 = Region(Rectangle((0, 4), (0, 2)), Rectangle((1, 2), (0, 4)), name="reg1")

reg2 = Region(Rectangle((0, 4), (0, 2)), Rectangle((1, 2), (1, 4)), name="reg2")

reg3 = Region(Rectangle((0, 4), (0, 2)), Rectangle((1, 2), (0, 3)), name="reg3")

assert reg1.montecarlo_equality(reg2)

assert not reg1.montecarlo_equality(reg3)

There are three main operations on rectangles: intersection, union, and difference. Among them, only intersection is guaranteed to return another rectangle. In general, the union of two rectangles is ... two rectangles, and the difference between two rectangles is ... a whole lot of rectangles, as we will see. We let you implement rectangle equality, intersection, and membership of a point in a rectangle. Equality: Two rectangles R and T are equal if they have the same number of dimensions, and if for every dimension k, the interval of R along k is equal to the interval of T along k. For example, Rectangle((2, 3), (4, 5)) == Rectangle((2, 3), (4, 5)) Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) Rectangle((2, 3), (4, 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Intersection: The intersection is defined only if the rectangles have the same number of dimensions. The intersection is computed by taking the intersection of the intervals of the two rectangles for corresponding dimensions. Membership: For an n-dimensional point (20, 21, ...,xn) and an n-dimensional rectangle R, we have (220, 21, ..., In) E R if the point is in the region R. For instance: (2.5, 4.5) in Rectangle((2, 3), (4, 5)) (2, 3) in Rectangle((2, 3), (4, 5)) (1, 3) not in Rectangle((2, 3), (4, 5)) If the point and the rectangle have different dimensions, you can raise a TypeError. Question 5: Rectangle Equality 76] def rectangle_eq(self, other): ### YOUR CODE HERE Rectangle. _eq__ = rectangle_eq 79] # 5 points: tests for rectangle equality. assert Rectangle(2,3), (4, 5)Rectangle(2, 3)214, 522 assert Rectangle((2, 3), (4, 5)) != Rectangle((4, 5), (2, 3)) assert Rectangle((2, 3), (4, 5)) != Rectangle((2, 3), (4, 5), (6, 7)) Question 6: Rectangle Intersection [] ### Rectangle intersection def rectangle_and(self, other): if self.ndims != other.ndims: raise TypeError("The rectangles have different dimensions: {} and {}".format( self.ndims, other.ndims )) # Challenge: can you write this as a one-liner shorter than this comment is? # There are no bonus points, note. Just for the fun. ### YOUR CODE HERE Rectangle. __and__ = rectangle_and [ ] # Let's see how your rectangle intersection works. r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 3)) draw_rectangles(ri, r2) draw_rectangles (r1 & r2) [] # 10 points: tests for rectangle intersection. r1 = Rectangle((2, 3), (0, 4)) r2 = Rectangle((@, 4), (1, 3)) assert r1 & r2 == Rectangle((2, 3), (1, 3)) r1 = Rectangle((2, 3), (2, 4)) r2 = Rectangle((@, 4), (1, 5)) assert r1 & r2 == Rectangle((2, 3), (1, 4)) r1 = Rectangle((-1, 5), (@, 6)) r2 = Rectangle((@, 4), (-1, 3)) assert ri & r2 == Rectangle(0, 4), (0, 3)) r1 = Rectangle((2, 6), (0, 4)) r2 = Rectangle(0, 6), (2, 3)) assert ri & r2 == Rectangle((2, 6), (0, 3)) - Question 7: Point Membership in a Rectangle [] ### Membership of a point in a rectangle. def rectangle_contains(self, p): # The point is a tuple with one element per dimension of the rectangle. if len(p) != self.ndims: raise TypeError() ### YOUR CODE HERE Rectangle. _contains_ = rectangle_contains [] # 5 points: tests for membership. assert (2, 3) in Rectangle(0, 4), (1, 5)) assert (@, 4) in Rectangle((@, 4), (4, 5)) assert (4, 5) in Rectangle((@, 4), (4, 5)) assert (@, , 0) not in Rectangle((3, 4), (0, 3), (0, 8)) [] class Region (object): def __init__(self, *rectangles, name=None): "A region is initialized via a set of rectangles. *** self.rectangles = list(rectangles) if name is None: self.name = ".join( random.choices(string.ascii_letters + string.digits, k=8)) else: self.name = name def draw(self): draw_rectangles(*self.rectangles, prefix=self.name + ":") def _or_(self, other): "Union of regions."** return Region(*(self.rectangles + other.rectangles), name=self.name = "_union_" + other.name) [] # Let us try. r = Rectangle((@., 4.), (0., 4.), name="R") t = Rectangle((1.5, 3.5), (1., 5.), name="1") regi = Region(r, name="Regi") reg2 = Region(t, name="Reg2") (regi | reg2).draw() Question 8: Membership of a Point in a Region A point belongs into a region if it belongs into some rectangle of the region. We let you implement this. [] ### Membership of a point in a region def region_contains(self, p): ### YOUR CODE HERE Region. __contains__ - region_contains [] assert (2, 1) in Region (Rectangle((@, 2), (0, 3)), Rectangle((4, 6), (5, 8))) assert (2, 1) not in Region (Rectangle((@, 1), (, 3)), Rectangle((4, 6), (5, 8))) Question 9: Compute Bounding Boxes First, write a method bounding_box of a region, which returns the bounding box contains the region. a rectangle. The bounding box is the smallest rectangle that [ ] ### compute the bounding box of a region def region_bounding_box(self): "*"Returns the bounding box of the region, as a rectangle. This returns None if the region does not contain any rectangle." if len(self.rectangles) == 0: return None ### YOUR CODE HERE Region.bounding_box = property (region_bounding_box) [] # 10 points: tests for bounding boxes reg = Region (Rectangle((@, 2), (1, 3)), Rectangle((4, 6), (5, 8))) assert reg. bounding_box == Rectangle((@, 6), (1, 8)) reg = Region Rectangle((@, 5), (4, 5), (1, 9)), Rectangle((4, 20), (-2, 3), (4, 21)), Rectangle((7, 99), (3, 7), (2, 3)) ) assert reg. bounding_box == Rectangle((@, 99), (-2, 7), (1, 21)) Question 10: Random Point in a Rectangle To select a random point from a rectangle, we just need to return a tuple formed by choosing a random point from each of the rectangle's intervals. We leave this to you. Remember that the intervals of a rectangle self are in self.intervals [] ### Random point of a rectangle def rectangle_random_point(self): ### YOUR CODE HERE Rectangle.random_point = rectangle_random_point [] # 3 points: random point of a rectangle. r = Rectangle((@, 2), (1, 3)) for i in range(5): p = r.random_point() assert isinstance(P, tuple) assert len(P) == 2 assert p in r print(P) [] # 3 points: random point of a rectangle. import numpy as np r = Rectangle((1, 2), (1, 6)) xs, ys = [], [] for in range(10000): p = r.random_point() assert p in r xs.append(p[@]) ys.append(P[1]) assert np.std(xs) * 4.9