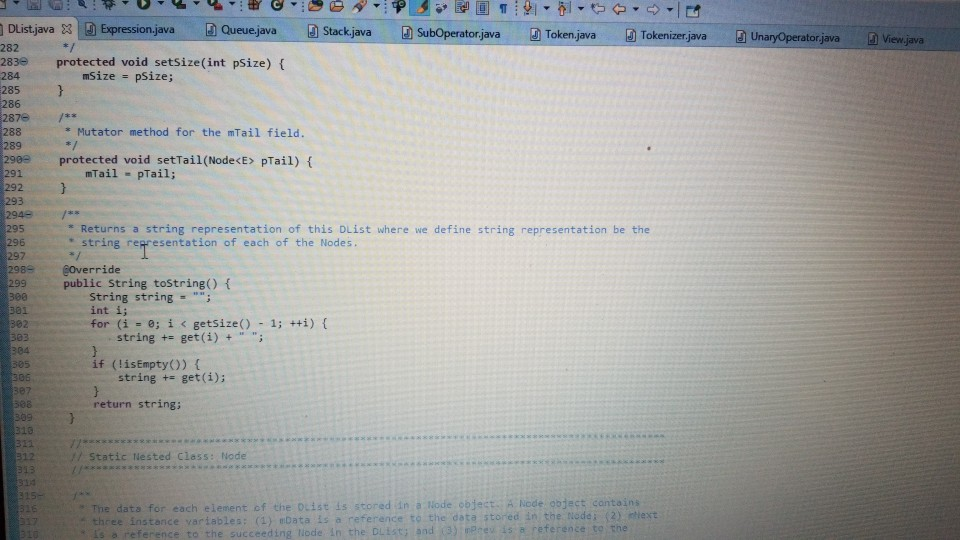
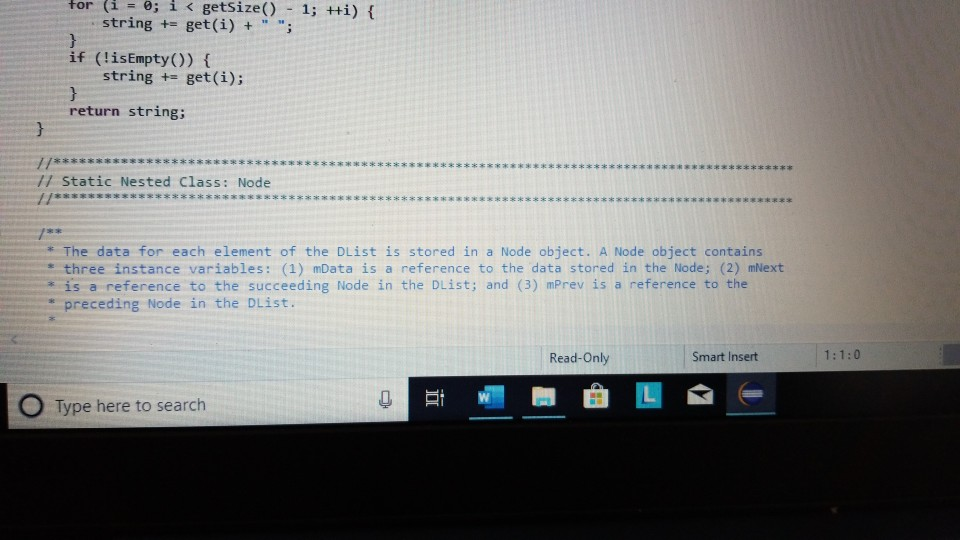
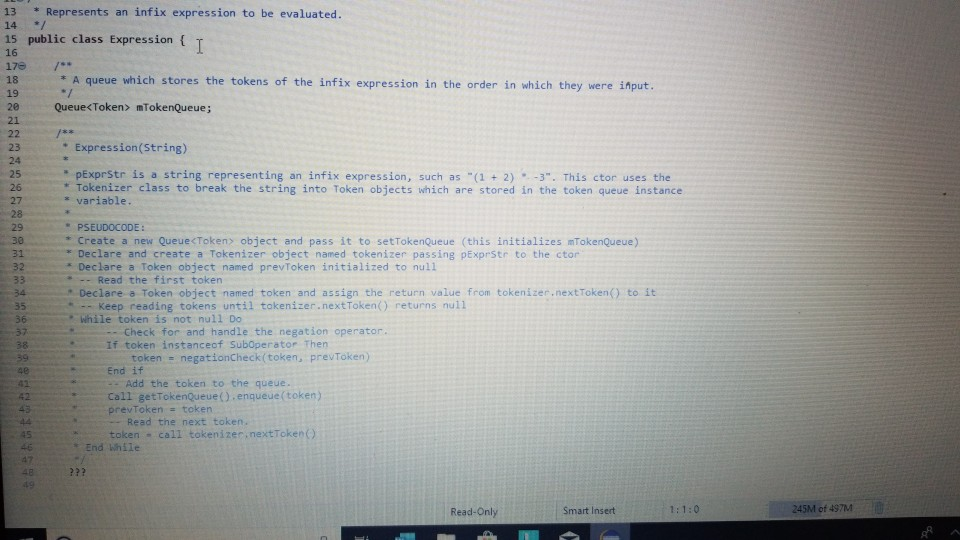
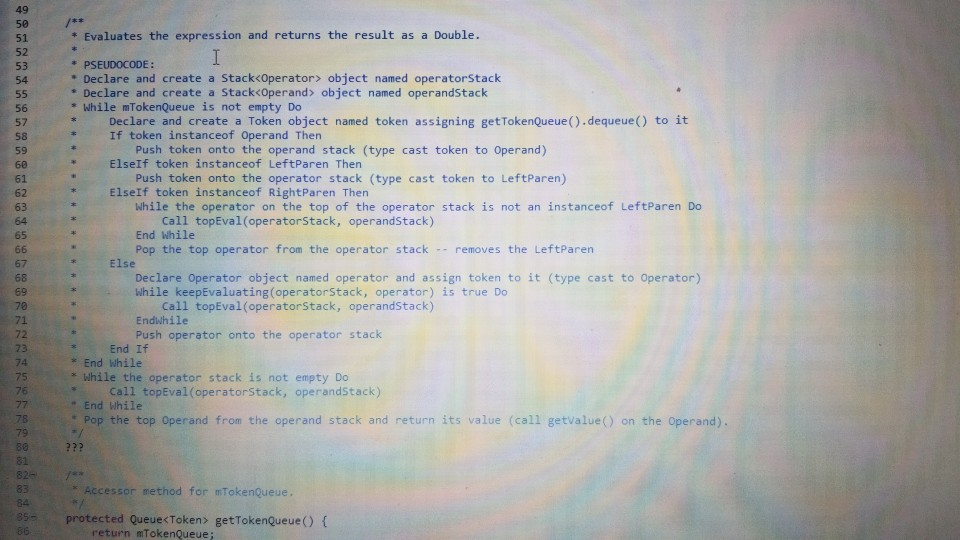
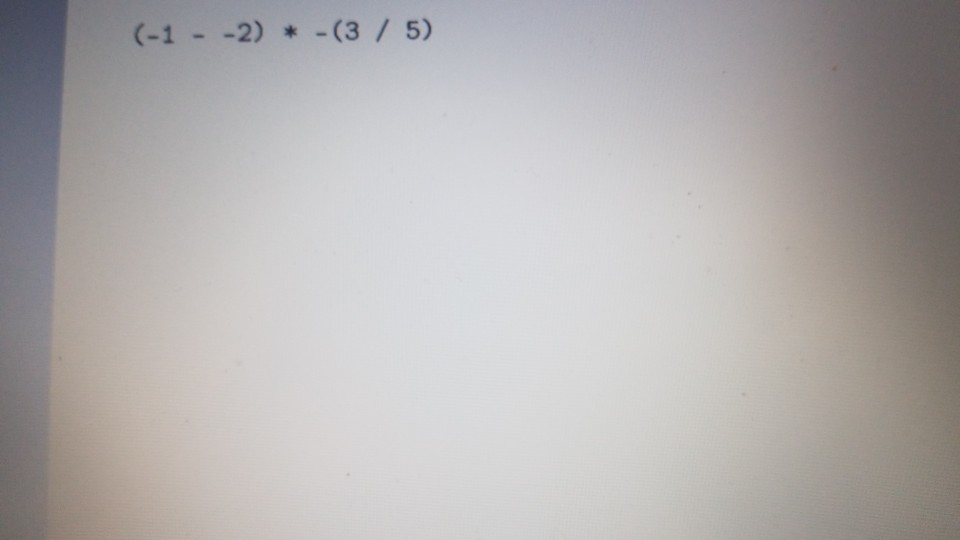Question: need help with the following program reach out if you need more information. . the trace I was given the classes I was given and
need help with the following program reach out if you need more information. .
the trace I was given
the classes I was given and need help coding
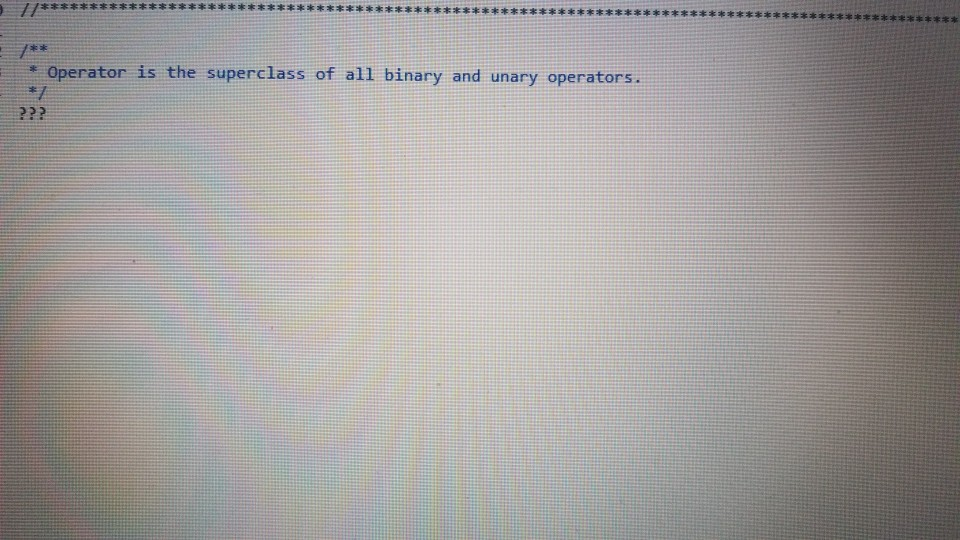
operator
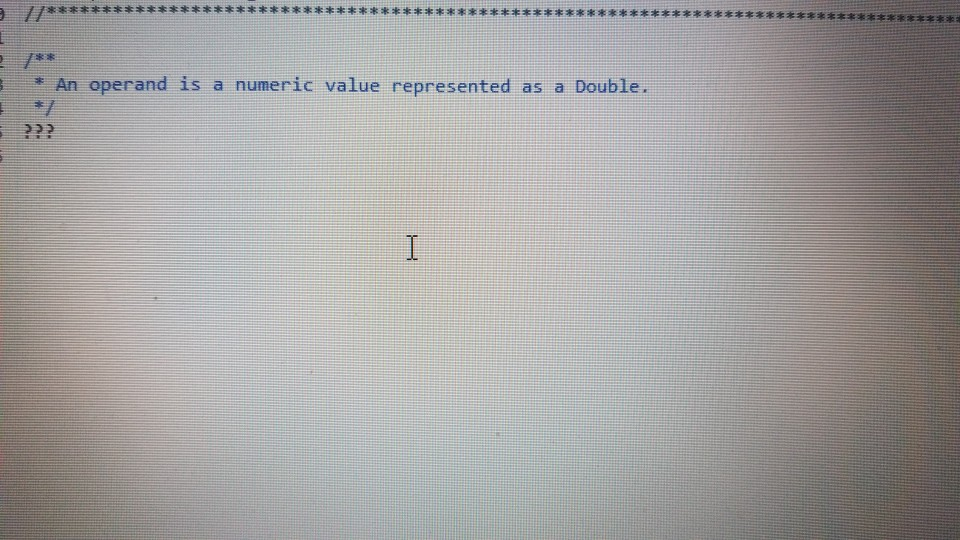
operand
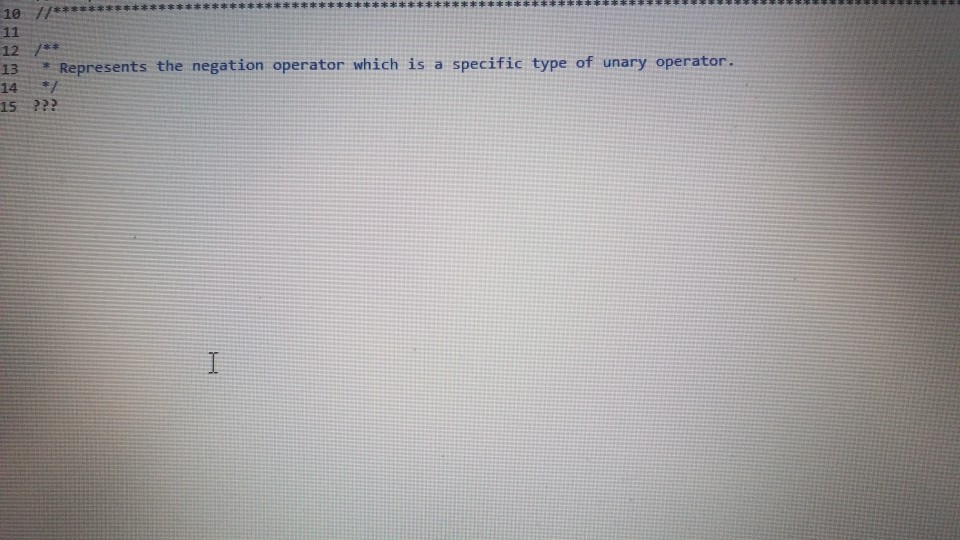
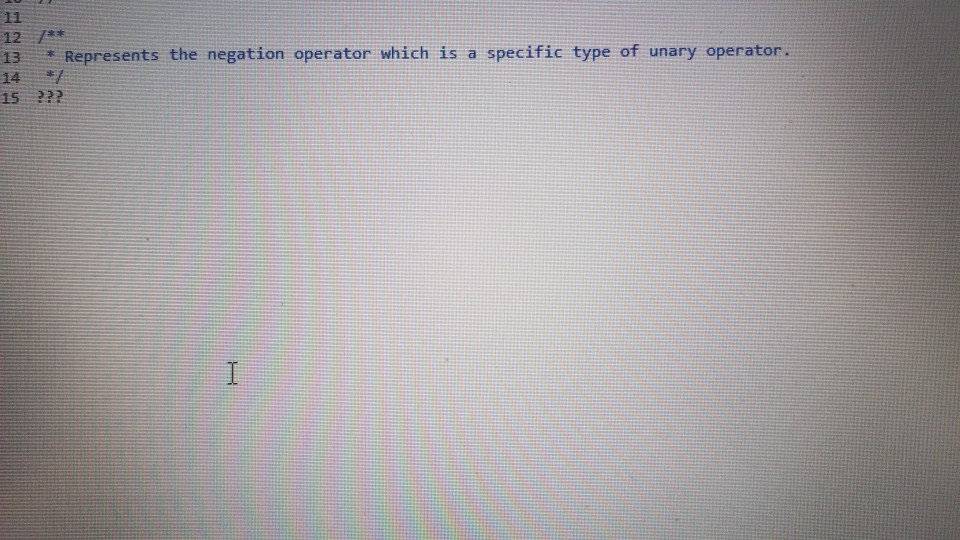
neg operator
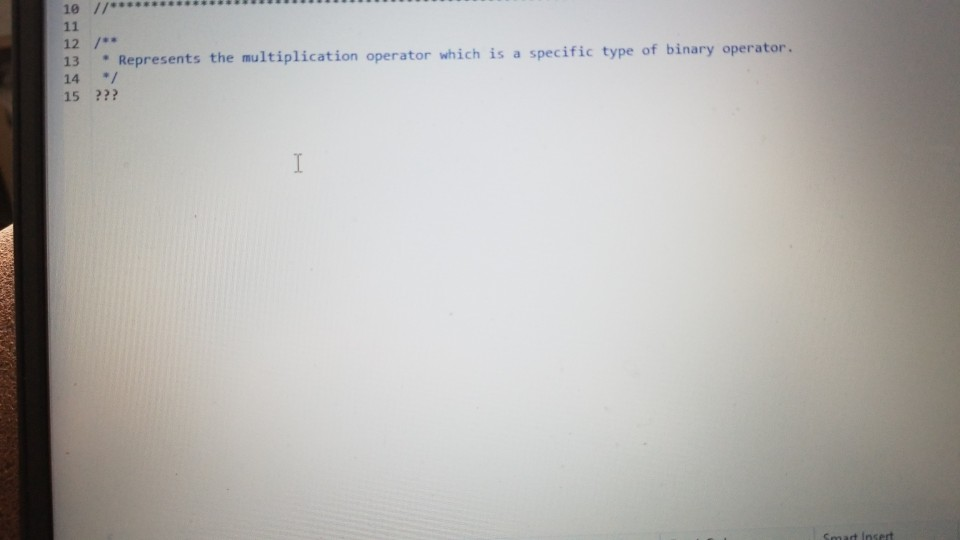
multiplication
main
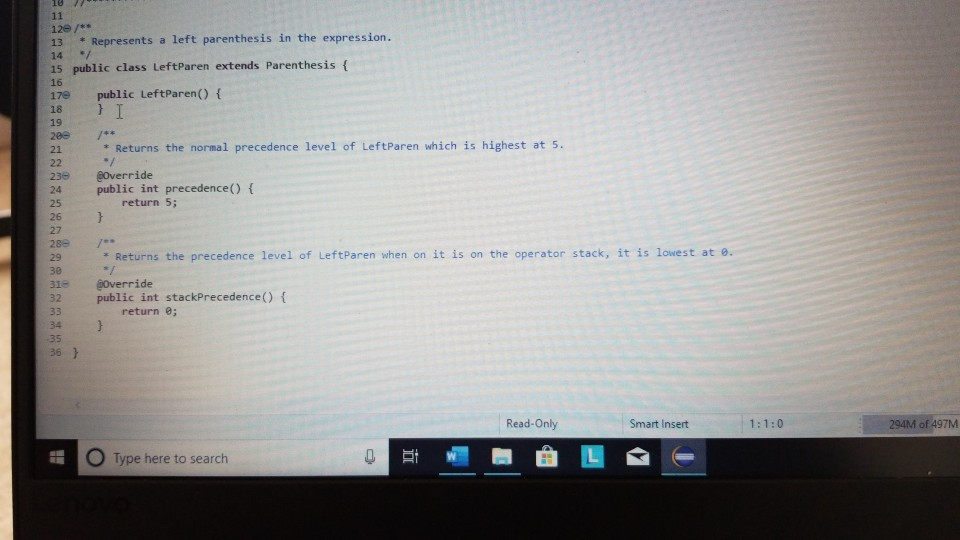
left paren
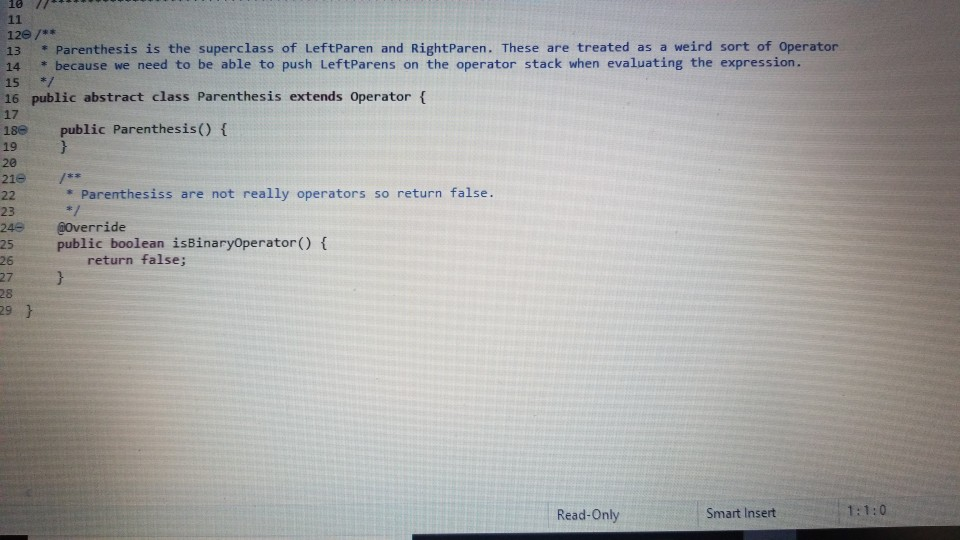
parenthesis
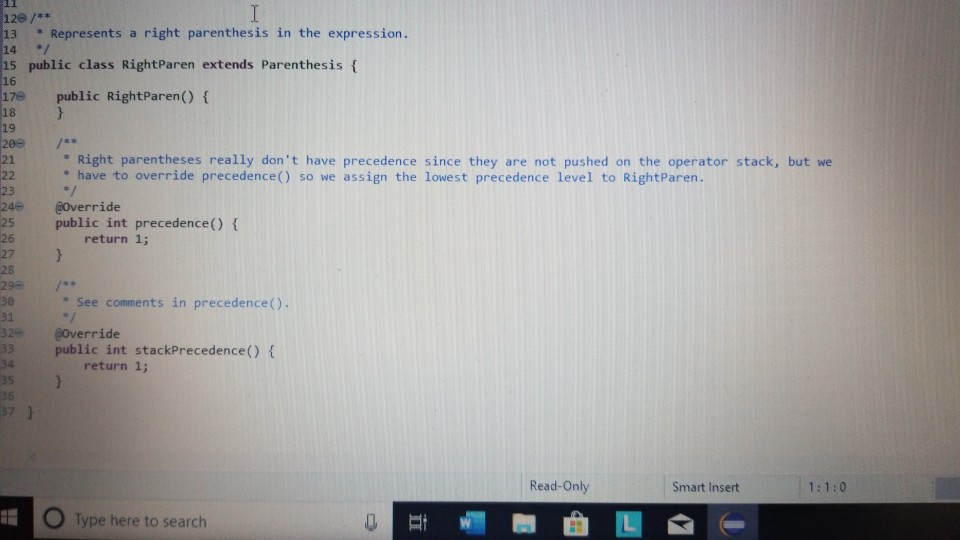
right Paren
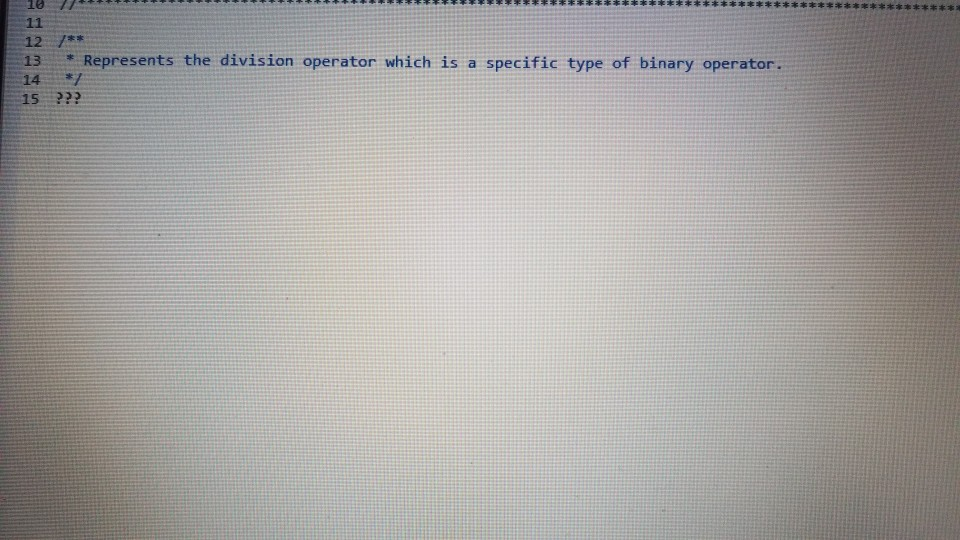
div
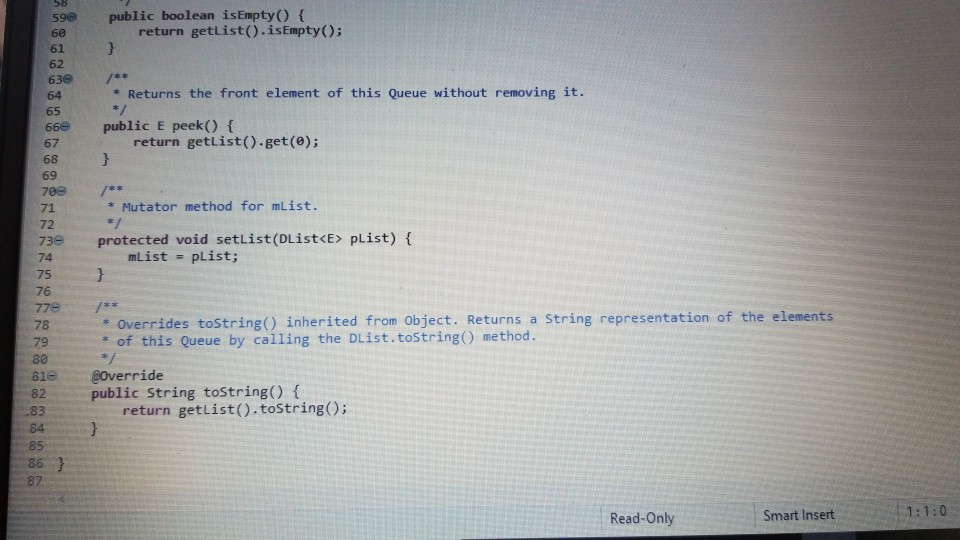
binary
add
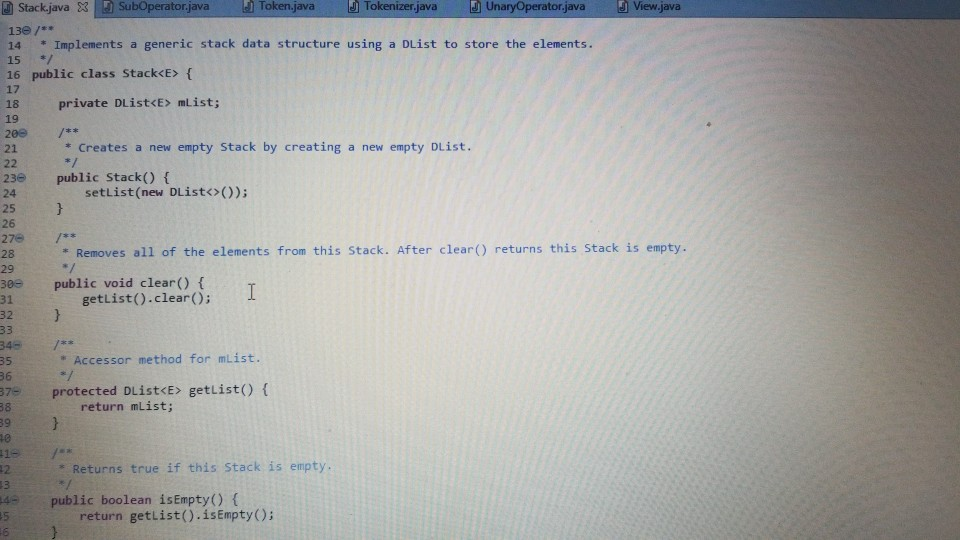
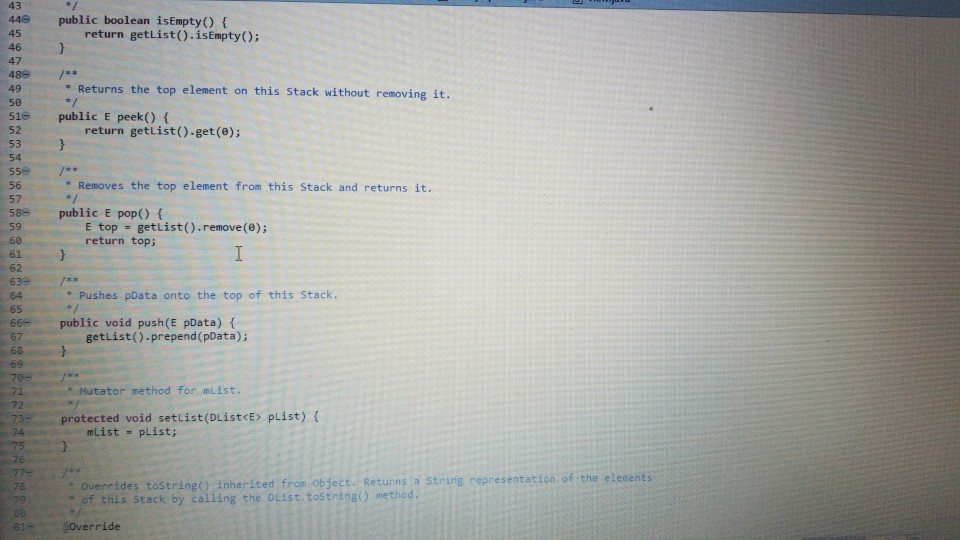
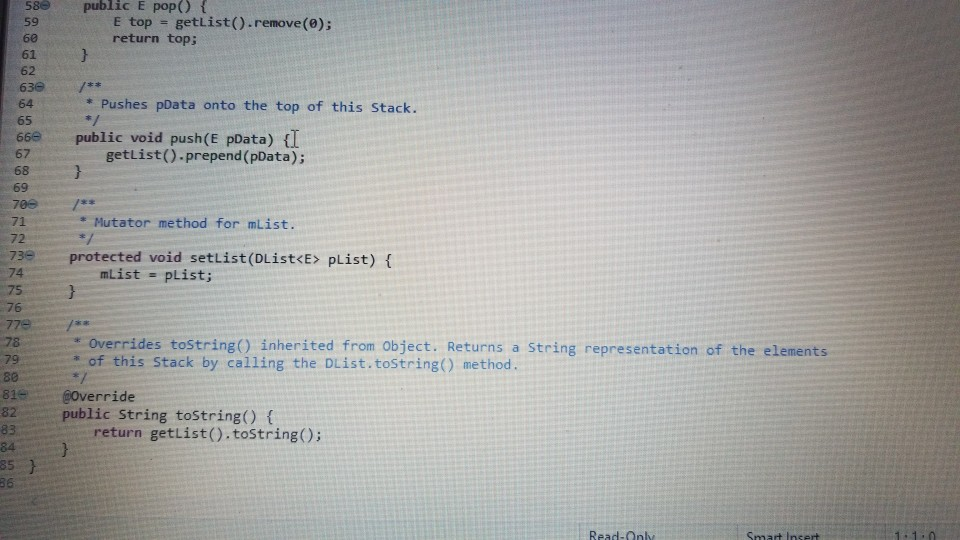
dlist
expressions
queue E
Stack
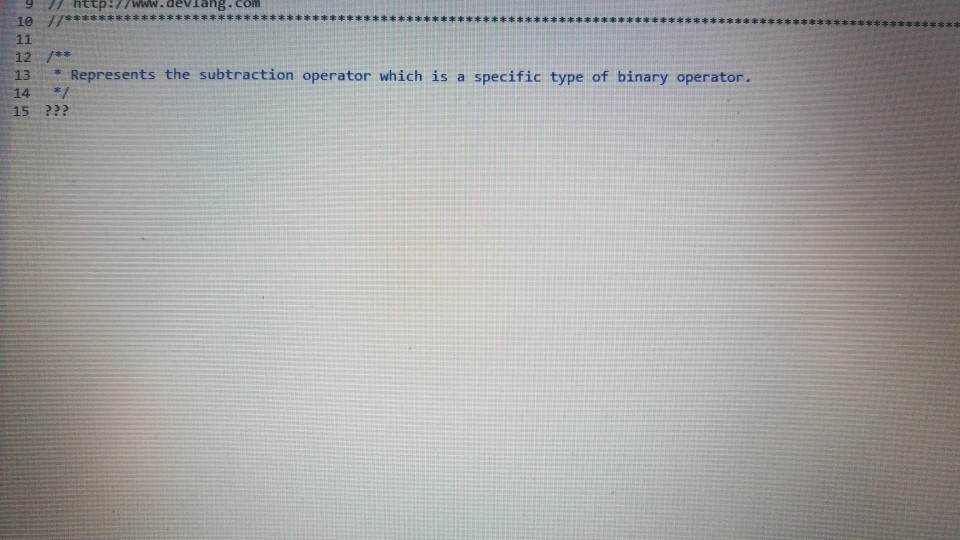
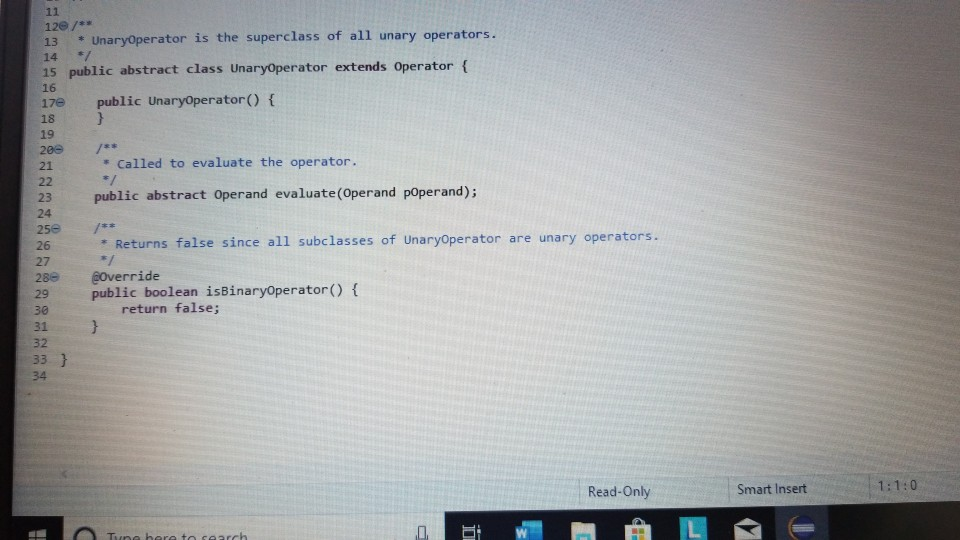
sub
token
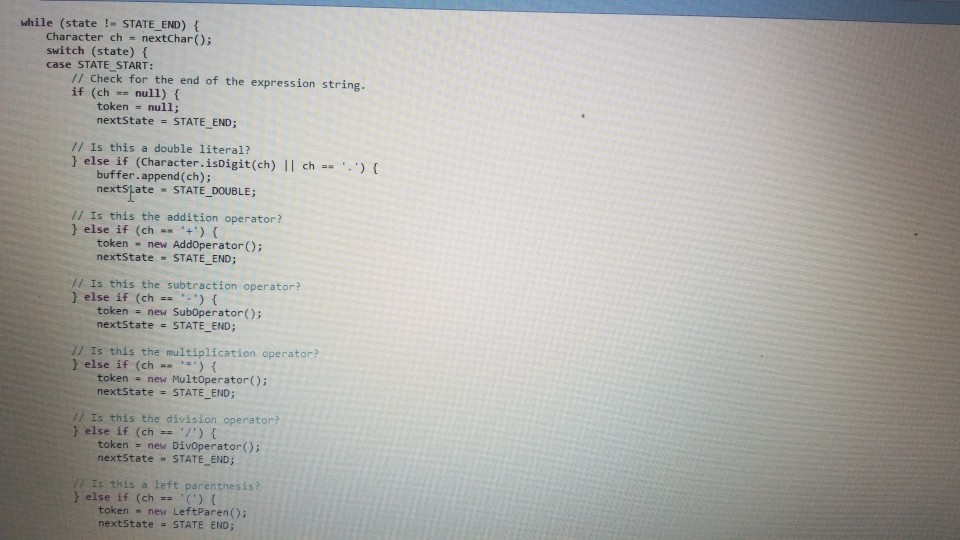
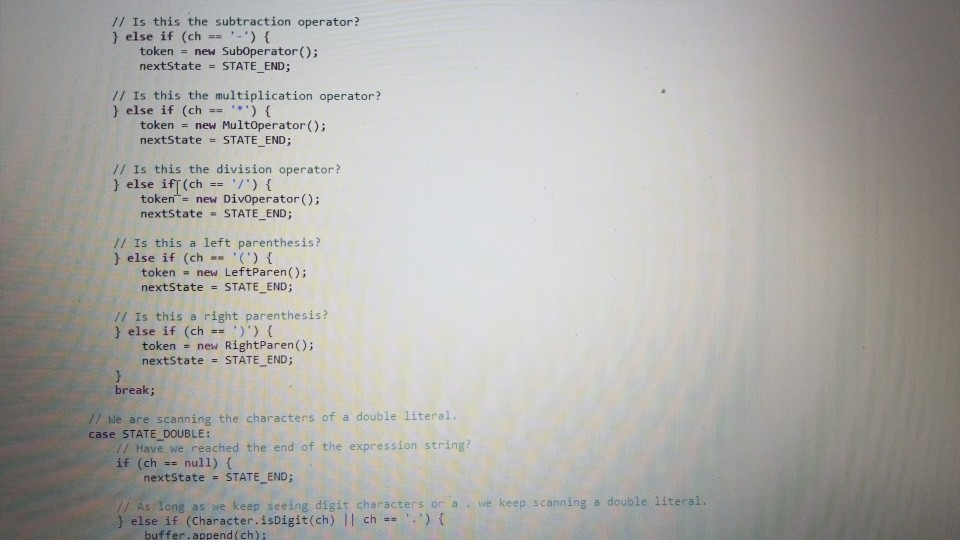
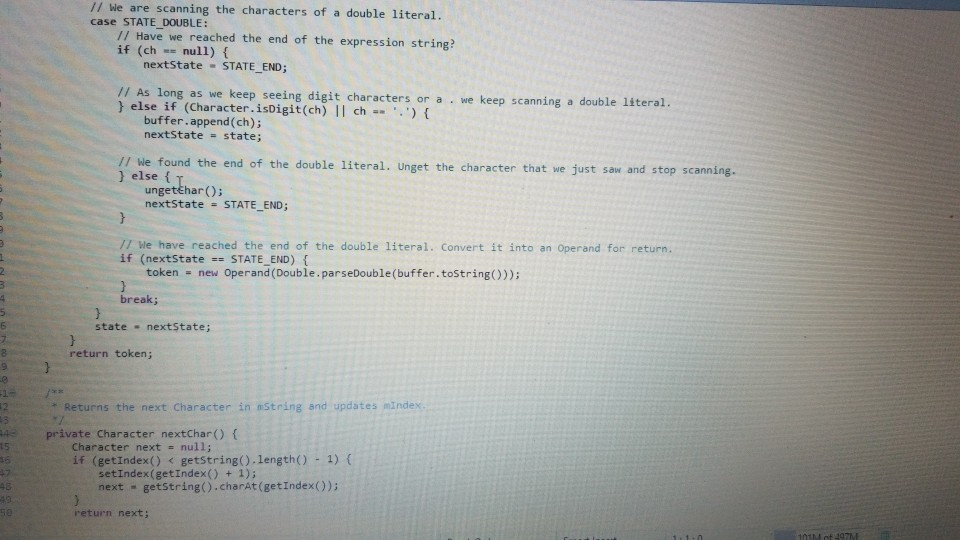
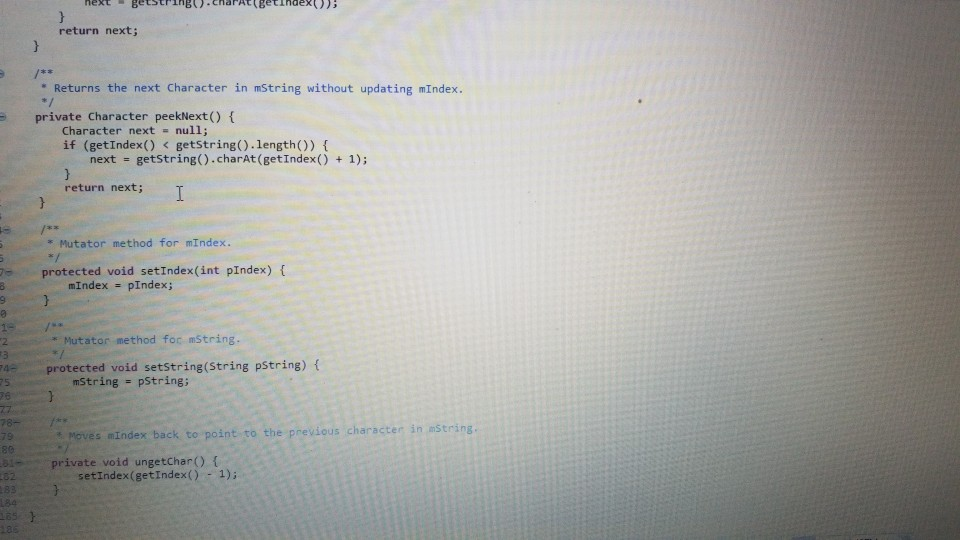
tokenizer
unary
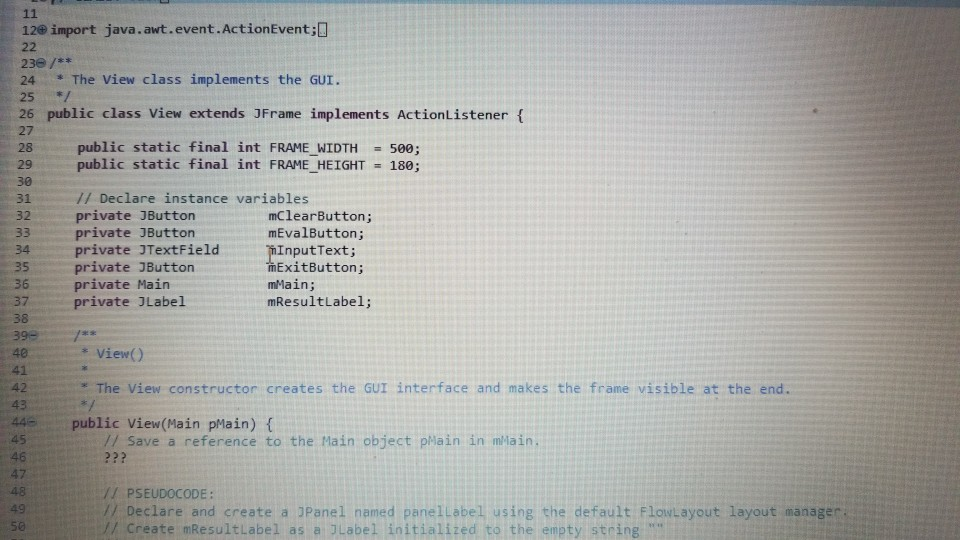
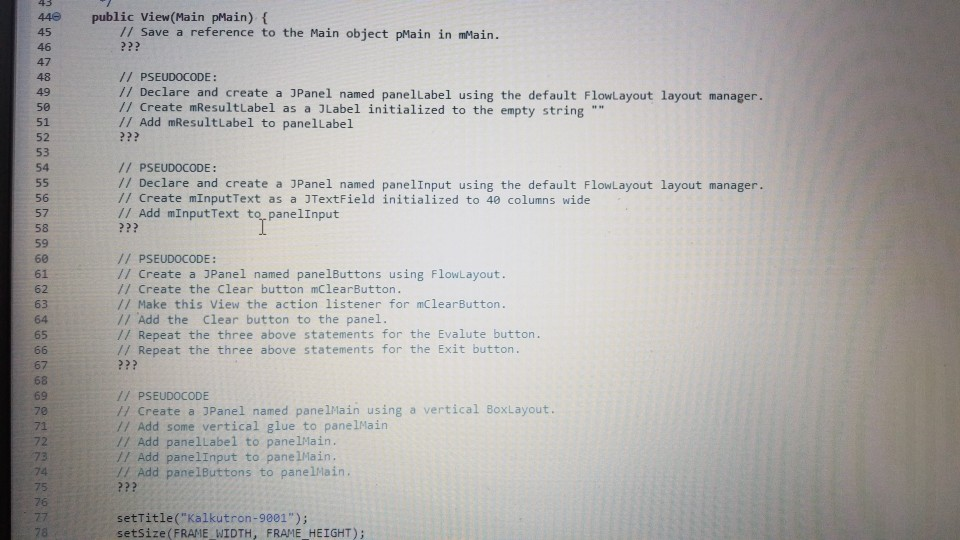
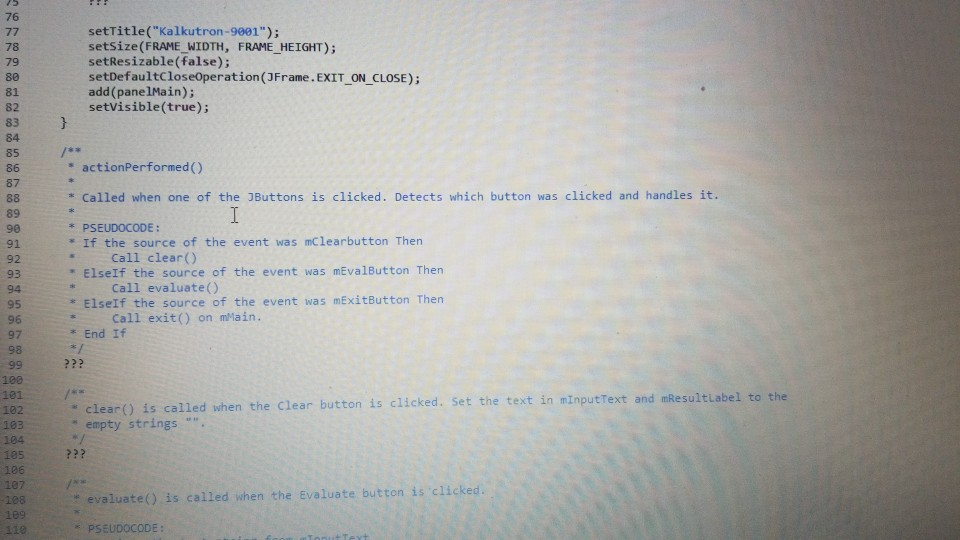
view
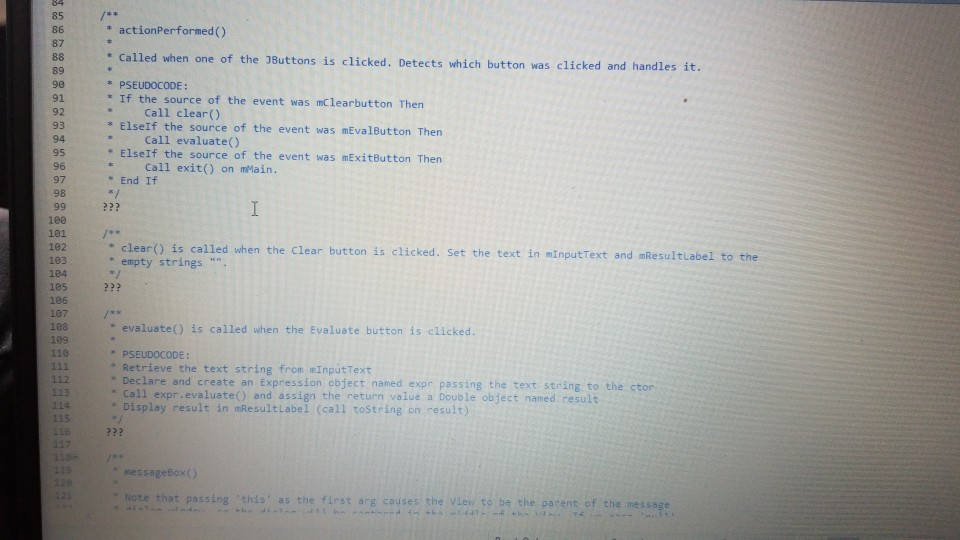
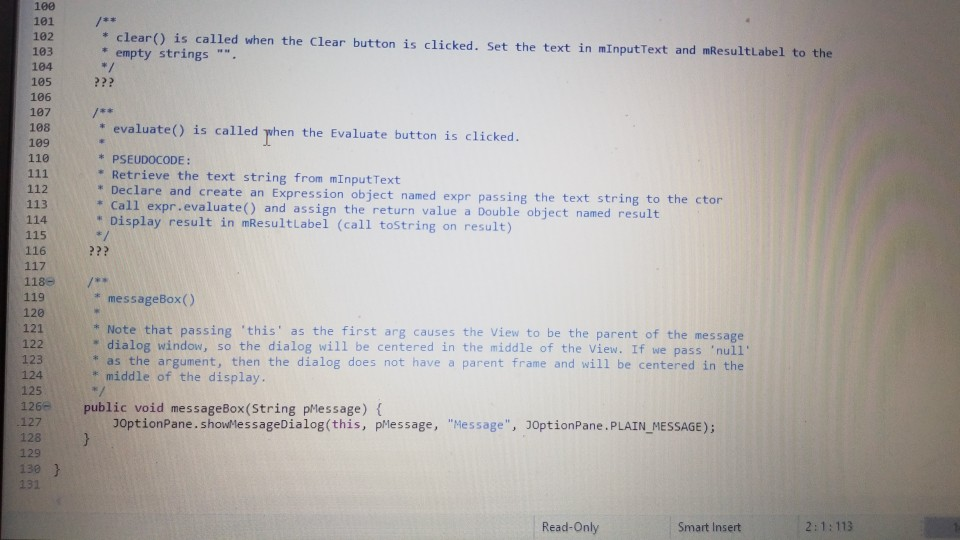
please help me with these and let me know if you have any questions
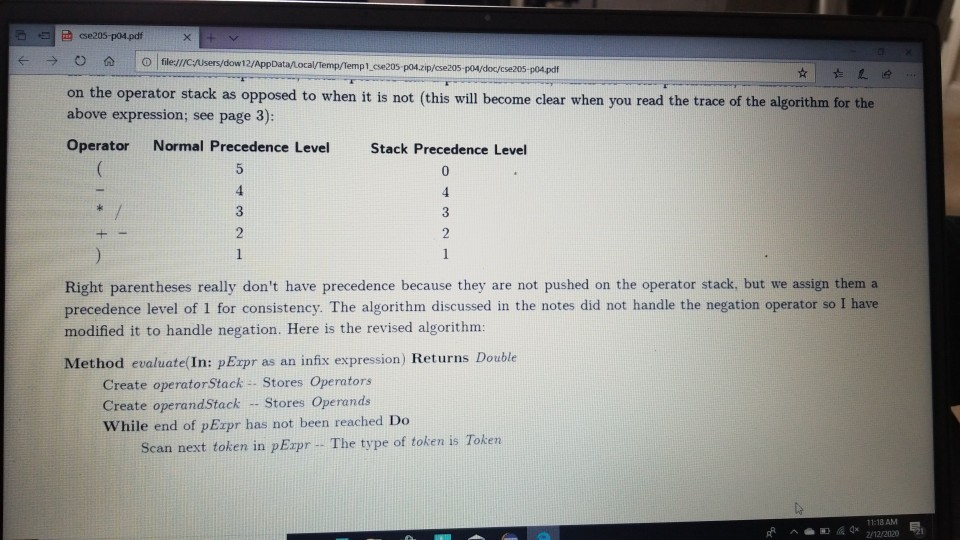
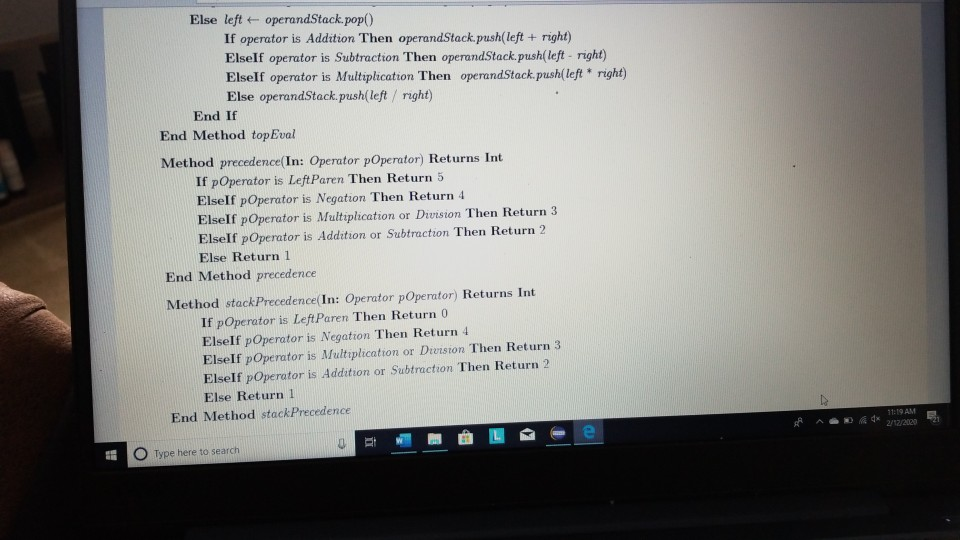
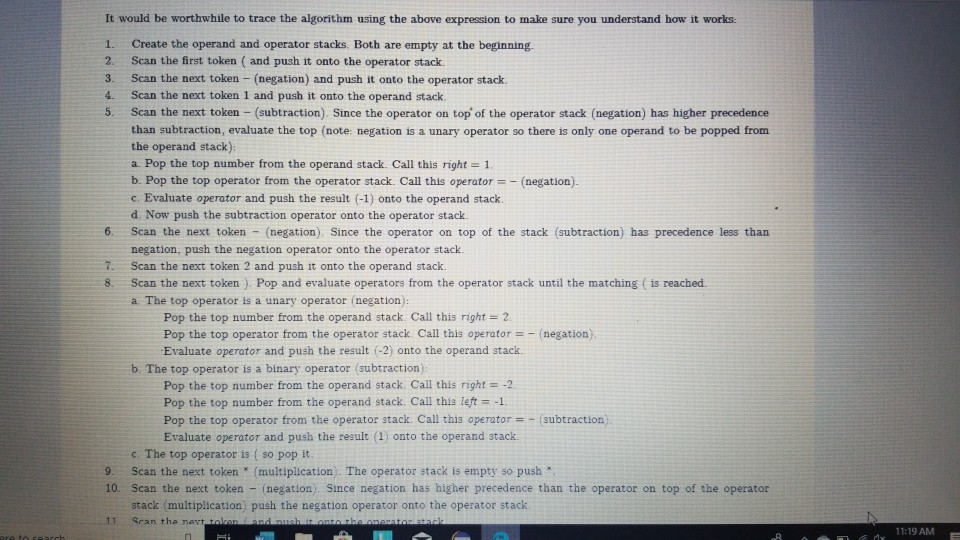
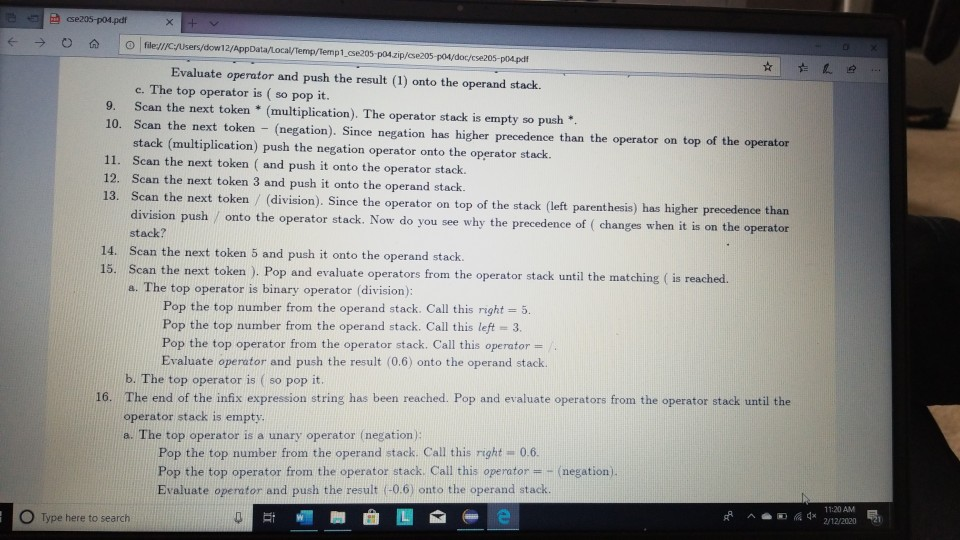
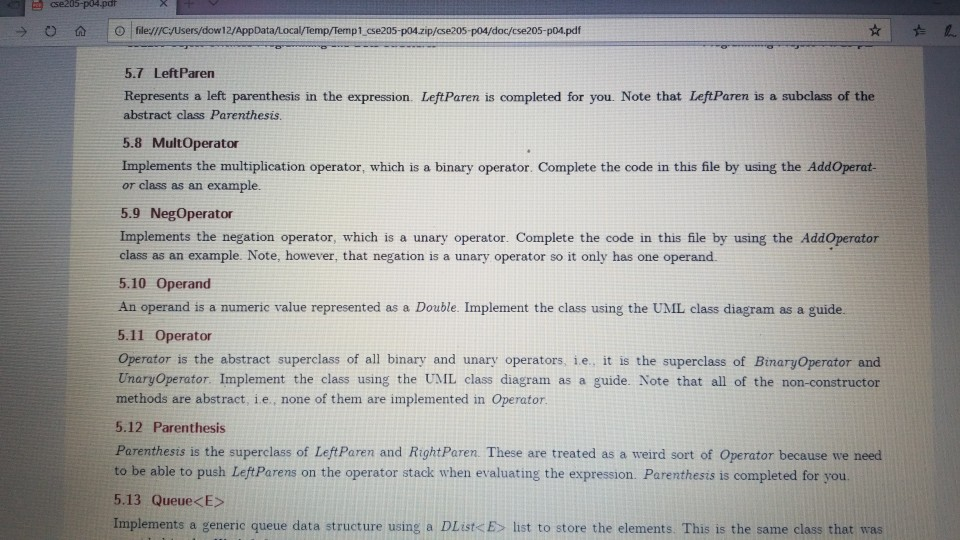
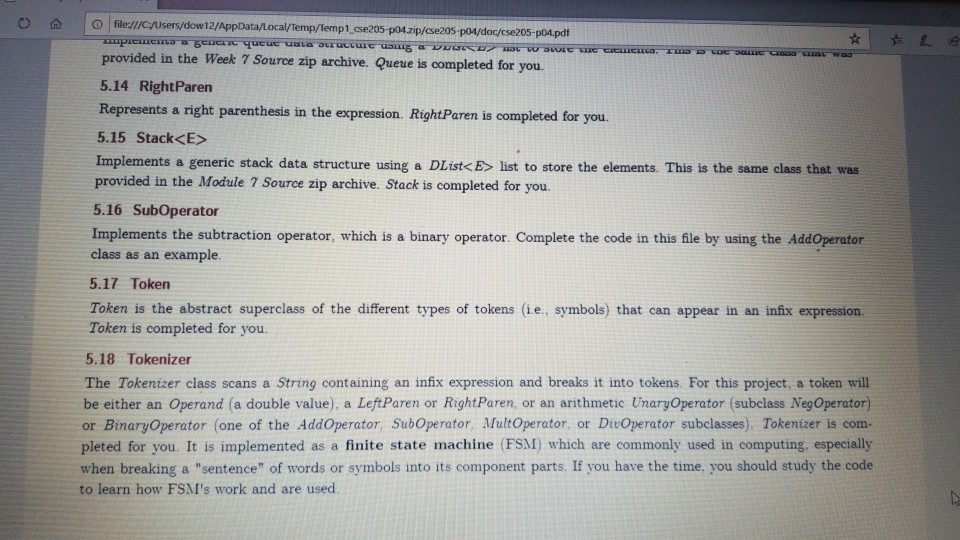
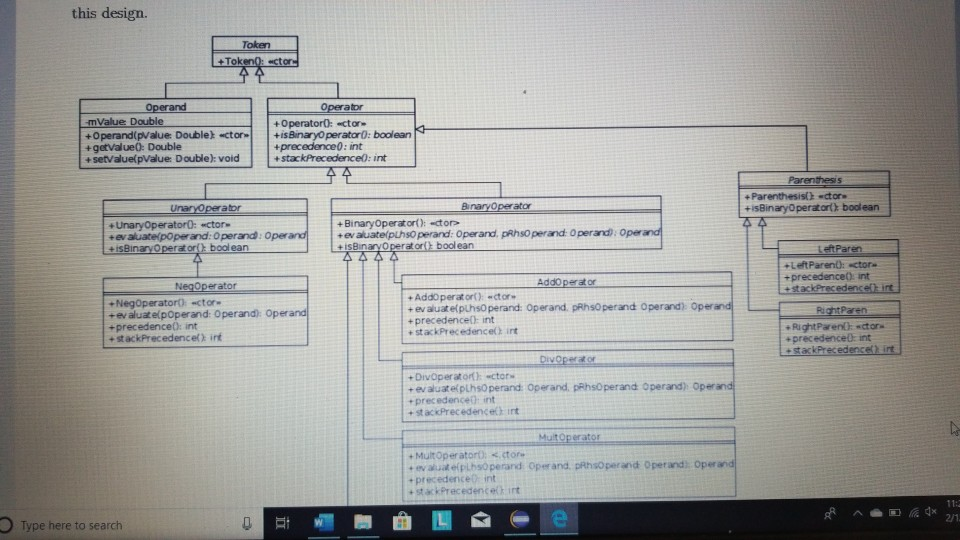
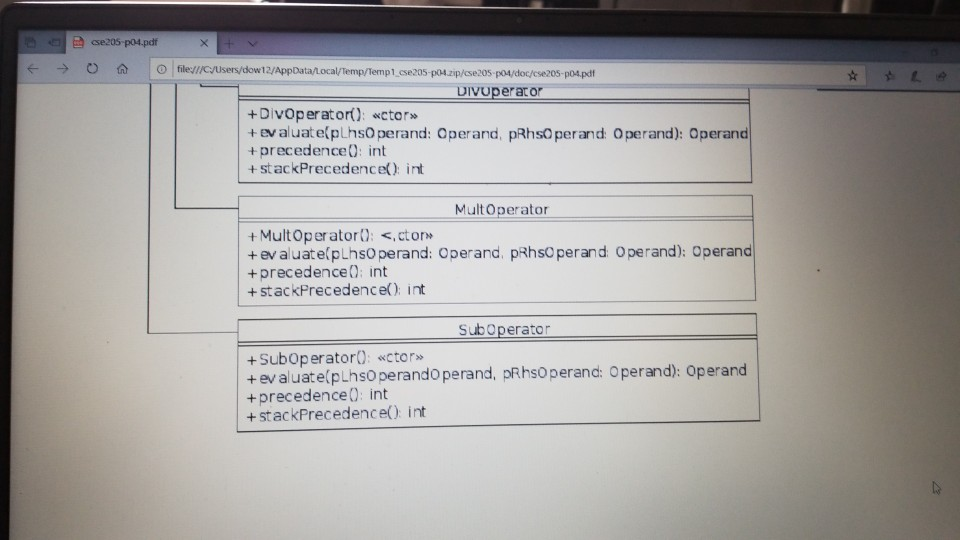
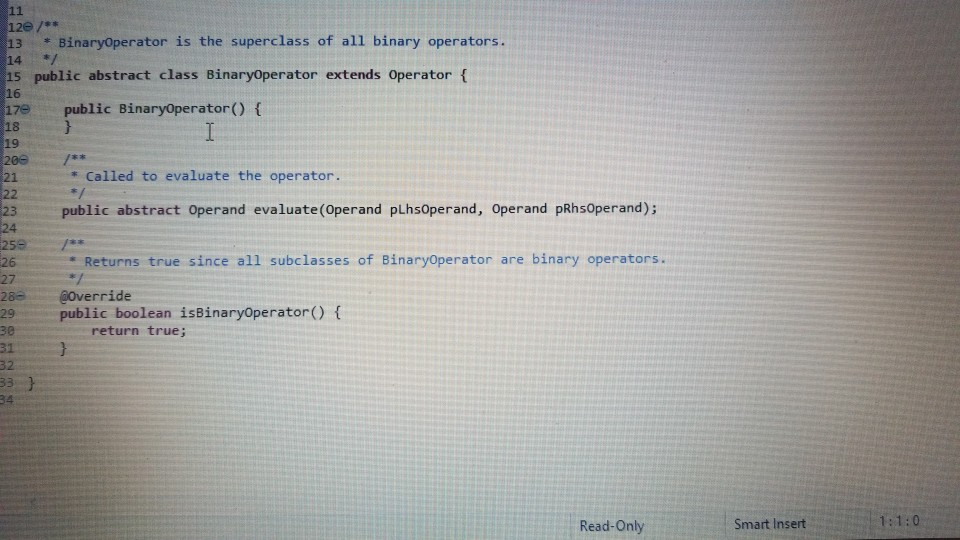
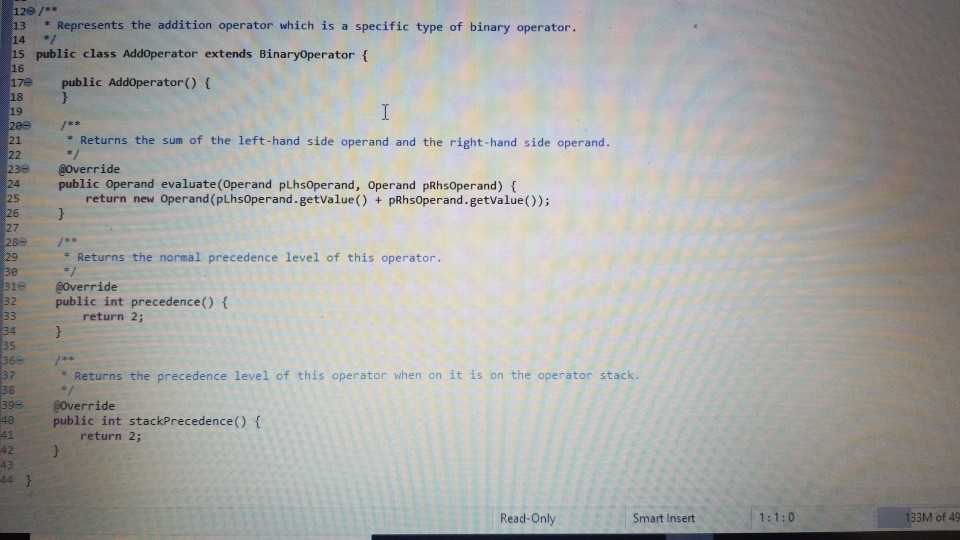
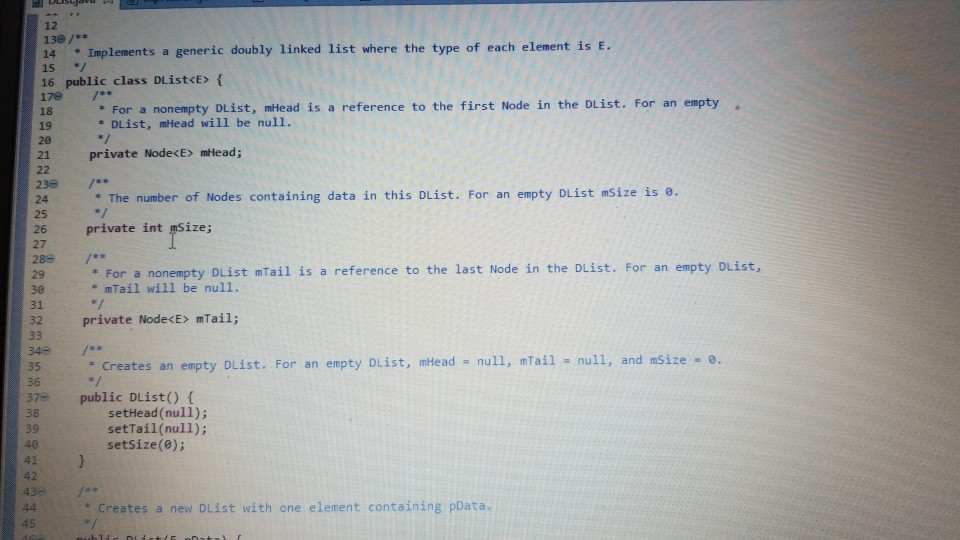
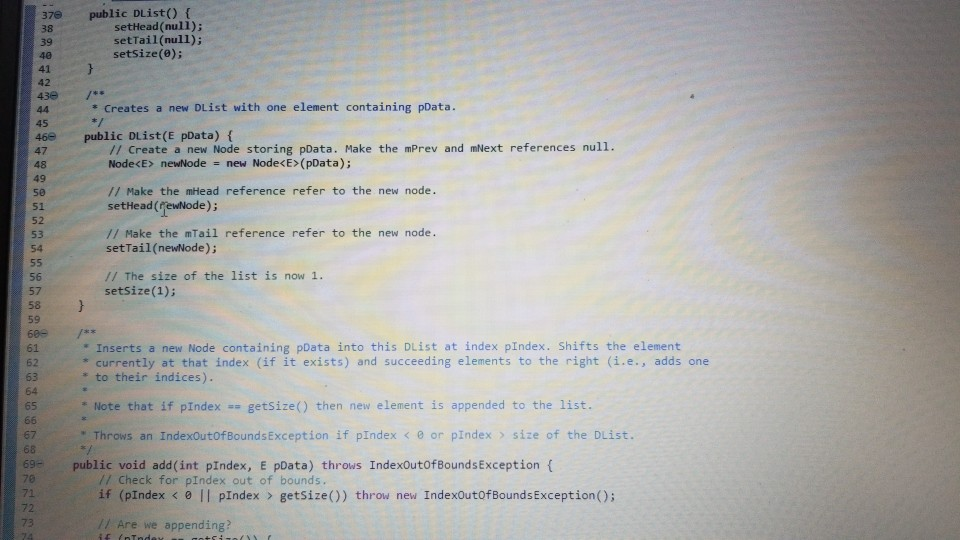
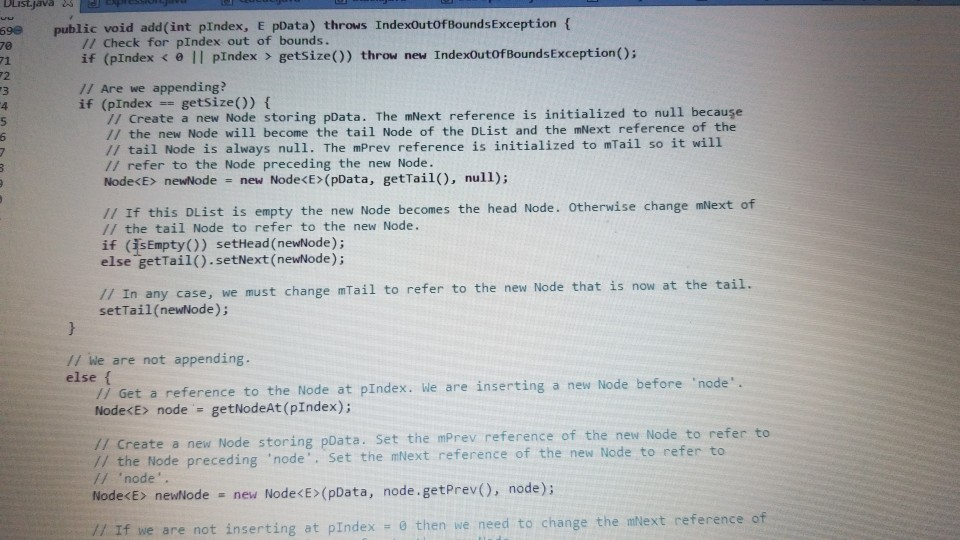
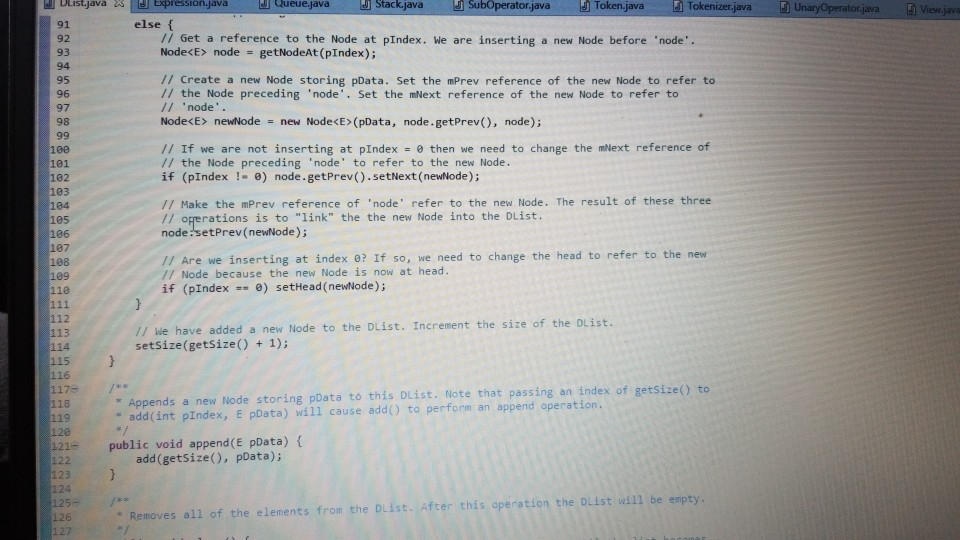
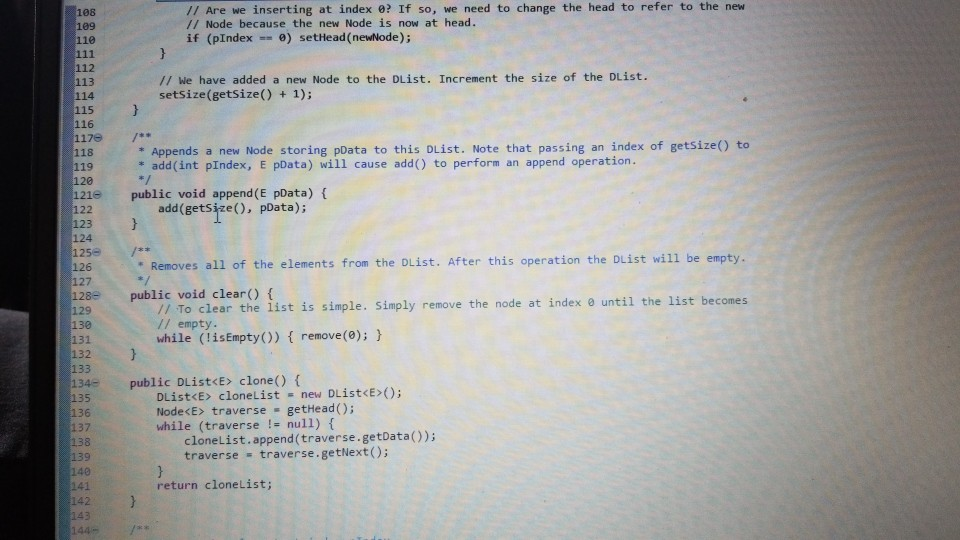
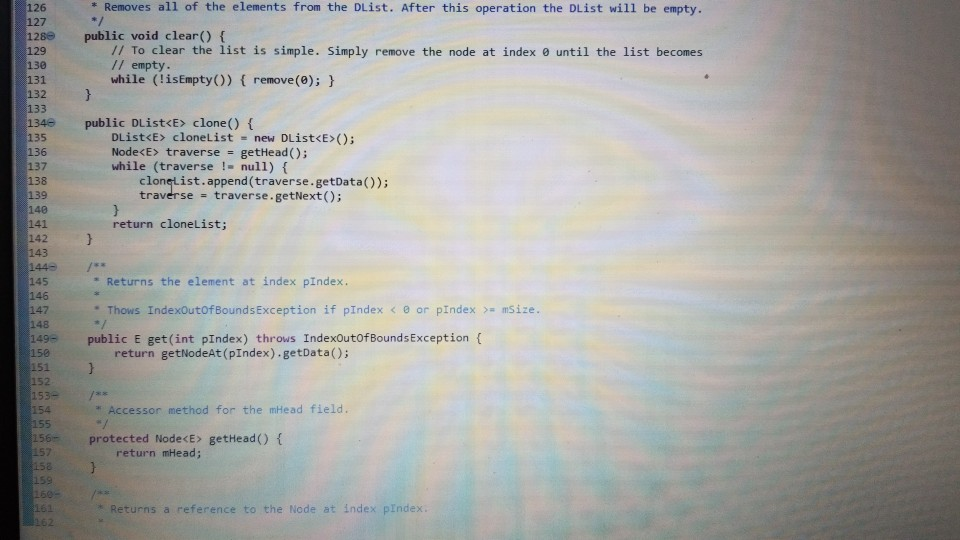
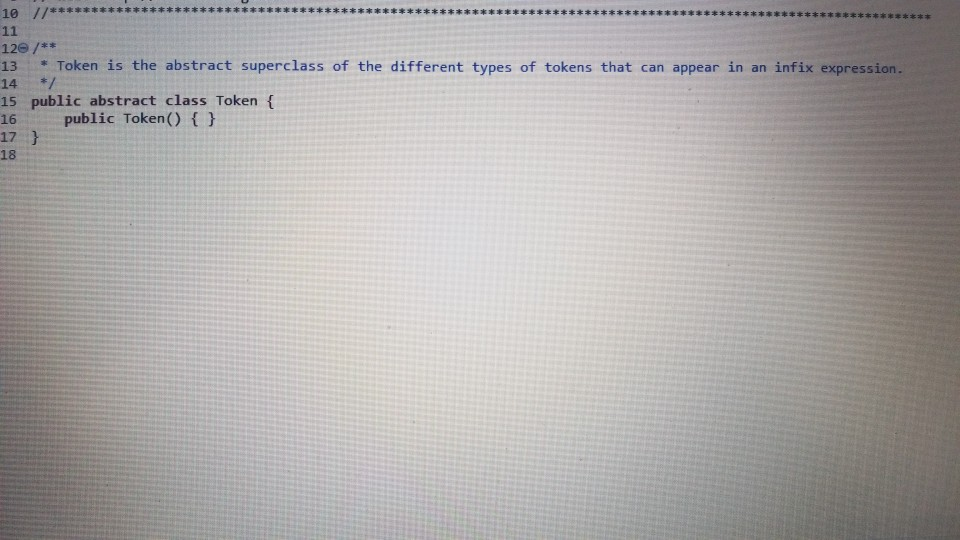
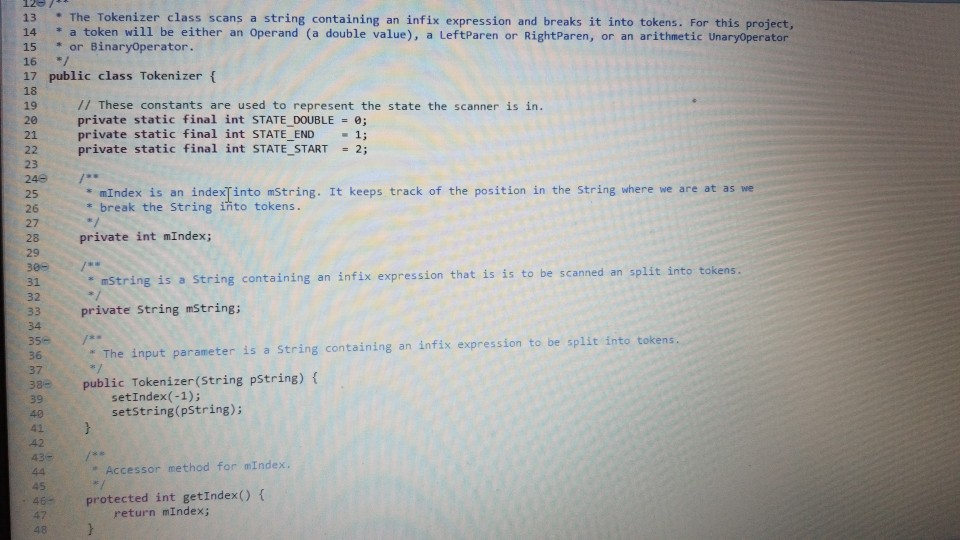
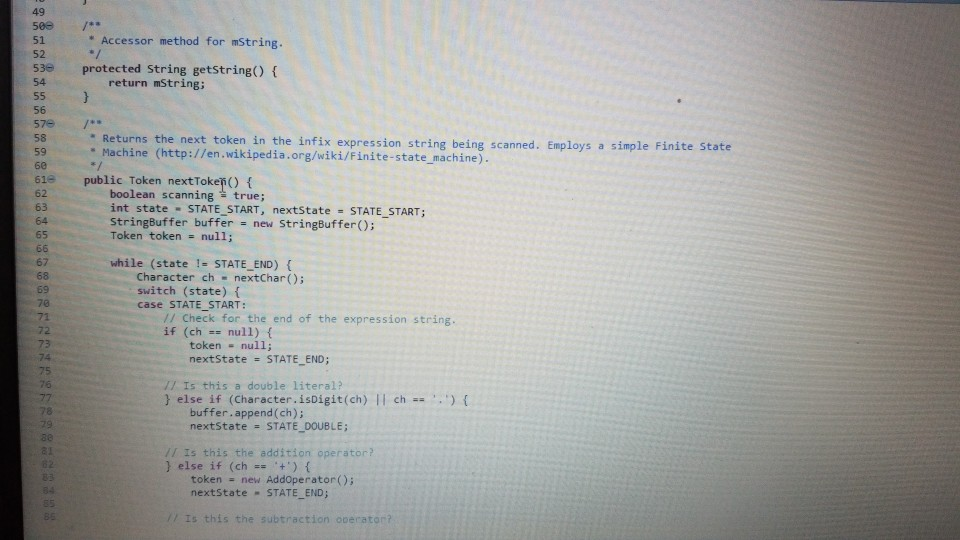
1 Submission Instructions Create a folder named avardeid pol where arutted in your ASURITE mer (for emple, if your ASURITEN yorits then your folder would be named amith-pod) and copy all of your fawn source code files to this folder. Do not copy the class file or any other filen. Next, comprese the amurid pol folder creating a xip archive file named arredo zip (e.6. jamith6-p0d.zip). Upload arterid p01.sip on the Csavae Module 7: P2 Dae m inion page before the project deadline. Please see the Course Summary mction on the Sllalue page in Canvas for the deadline. Consult the Syllabu for the late and academic integrity policie 2 Learning Objectives 1. Complete all of the learning objects of the previous projects 2. To implement a GUI interface and respond to action eventa 3. To use the linloed list, atack, and queue classes 3 Background In the lectural notes and video lectures for Stacks and Queues : Section 3-7 we discussed an application that evaluate an srithmetic expression written in infix notation rucha (-1--2) -(3/5) Infix notation is the urual algebraic notation that we are all familiar with where a binary operator a binary operatoria operator that has two operanda) is written between the left-hand and right-hand operande. For example, in the expression above, the left-hand operand of the rubtraction operatorie -1 and the right-hand operand sa-2. Some operators, ruch 22 the negation operator, are unary operatore meaning there is only one operand (t one). For negation, the operandia written to the right of the negation operator. Therefore, this expression contains aix operatore: negation, rubtraction negation, multiplication, negation, and division In the algorithm that evaluate the expression, we also treat a left parenthese as an operator, which it is not, but during the evaluation we have to push left parentheses onto the operator stack In an infix arithmetic expression, each operator has a precedence level, which for a left parenthera ta different when it a on the operator stack as opposed to when it is not this will become clear when you read the trace of the algorithm for the above excprension: see page 3 Operator Normal Precedence Level Stack Precedence Level cse205-po.pdf 0 file:///C:/Users/dow 12/AppData/local/temp/Templ_cse205-p04.zip/cse205-p04/doc/cse205-p04.pdf on the operator stack as opposed to when it is not (this will become clear when you read the trace of the algorithm for the above expression; see page 3): Operator Normal Precedence Level Stack Precedence Level No * Right parentheses really don't have precedence because they are not pushed on the operator stack, but we assign them a precedence level of 1 for consistency. The algorithm discussed in the notes did not handle the negation operator so I have modified it to handle negation. Here is the revised algorithm: Method evaluate(In: pExpr as an infix expression) Returns Double Create operator Stack - Stores Operators Create operandStack -- Stores Operands While end of pExpr has not been reached Do Scan next token in pExpr-. The type of token is Token A 11:18 AM 64* 2/12/2020 51 If token is an operand Then Convert token to Operand object named number operandStack.push(number) ElseIf token is an InstanceOf LeftParen Then Convert token to LeftParen object named paren operator Stack.push(paren) ElseIf token is an InstanceOf Right Paren Then While not operator Stack peek() is an InstanceOf Left Paren Do topEval operator Stack.pop() -- Pops the LeftParen ElseIf token is Negation, Addition, Subtraction, Multiplication, or Division Then Convert token to Operator object named operator While keep Evaluating returns True Do topEvall) operator Stack.push(op) End While While not operator Stack.isEmpty Do top Eval) Return operandStack.pop() -- the result of evaluating the expression End Method evaluate Method keep Evaluating Returns True or False If operator Stack.is Empty() Then Return False Else Return stack Precedence operator Stack peek()) 2 precedence operator) End Method keep Evaluating Method top Eval) Returns Nothing right - operandStack.pop) operator - operator Stack.popo If operator is Negation Then operandStock push(-right) Else left - operand Stock pop) If operator is Addition Then operandStack push left-right) ElseIf operator is Subtraction Then operandStock.push left right) ElseIf operator is Multiplication Then operandStack.push(left* right) Else left + operandStack.pop() If operator is Addition Then operandStack.push(left + right) ElseIf operator is Subtraction Then operandStack.push(left-right) ElseIf operator is Multiplication Then operandStack.push(left * right) Else operandStack.push(left/right) End If End Method topEval Method precedence(In: Operator pOperator) Returns Int If pOperator is Left Paren Then Return 5 ElseIf pOperator is Negation Then Return 4 ElseIf pOperator is Multiplication or Division Then Return 3 ElseIf pOperator is Addition or Subtraction Then Return 2 Else Return 1 End Method precedence Method stack Precedence In: Operator pOperator) Returns Int If pOperator is Left Paren Then Return 0 ElseIf pOperator is Negation Then Return 4 ElseIf pOperator is Multiplication or Division Then Return 3 ElseIf pOperator is Addition or Subtraction Then Return 2 Else Return 1 End Method stack Precedence 11:19 AM BAA D 2/12/2020 21 Type here to search It would be worthwhile to trace the algorithm using the above expression to make sure you understand how it works: 1. Create the operand and operator stacks. Both are empty at the beginning 2. Sean the first token and push it onto the operator stack 3. Scan the next token - (negation) and push it onto the operator stack. Scan the next token 1 and push it onto the operand stack Scan the next token - (subtraction). Since the operator on top of the operator stack (negation) has higher precedence than subtraction, evaluate the top (note: negation is a unary operator so there is only one operand to be popped from the operand stack): a. Pop the top number from the operand stack. Call this right = 1 b. Pop the top operator from the operator stack. Call this operator = - (negation). c. Evaluate operator and push the result (-1) onto the operand stack d. Now push the subtraction operator onto the operator stack. Scan the next token - (negation). Since the operator on top of the stack (subtraction) has precedence less than negation, push the negation operator onto the operator stack Scan the next token 2 and push it onto the operand stack. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. a The top operator is a unary operator negation: Pop the top number from the operand stack. Call this right = 2 Pop the top operator from the operator stack Call this operator = - negation) Evaluate operator and push the result (-2) onto the operand stack. b. The top operator is a binary operator (subtraction): Pop the top number from the operand stack. Call this right = -2 Pop the top number from the operand stack. Call this left = -1 Pop the top operator from the operator stack. Call this operator = -(subtraction) Evaluate operator and push the result (1) onto the operand stack. c. The top operator is ( so pop it. 9. Scan the next token (multiplication. The operator stack is empty so push 10. Scan the next token - (negation). Since negation has higher precedence than the operator on top of the operator stack multiplication) push the negation operator onto the operator stack 11 Sran the next tolonlandisht onto the onesto stad SH 11:19 AM e E 0 c se205-po.pdf x + file:///C:/Users/dow12/AppData/local/temp/temp1_cse205-po4.zip/cse205-p04/doc/cse205-pot.pdf Evaluate operator and push the result (1) onto the operand stack. c. The top operator is ( so pop it. 9. Scan the next token * (multiplication). The operator stack is empty so push" 10. Scan the next token - (negation). Since negation has higher precedence than the operator on top of the operator stack (multiplication) push the negation operator onto the operator stack. 11. Scan the next token ( and push it onto the operator stack. 12. Scan the next token 3 and push it onto the operand stack. 13. Scan the next token/ (division). Since the operator on top of the stack (left parenthesis) has higher precedence than division push onto the operator stack. Now do you see why the precedence of changes when it is on the operator stack? 14. Scan the next token 5 and push it onto the operand stack. 15. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. 4. The top operator is binary operator (division): Pop the top number from the operand stack. Call this right = 5. Pop the top number from the operand stack. Call this left = 3. Pop the top operator from the operator stack. Call this operator = Evaluate operator and push the result (0.6) onto the operand stack. b. The top operator is so pop it. 16. The end of the infix expression string has been reached. Pop and evaluate operators from the operator stack until the operator stack is empty. a. The top operator is a unary operator (negation): Pop the top number from the operand stack. Call this right = 0.6. Pop the top operator from the operator stack. Call this operator = - (negation) Evaluate operator and push the result (-0.6) onto the operand stack. A D Type here to search O 11:20 AM 4* 2/12/2012021 b. The top operator is a binary operator (multiplication) Pop the top number from the operand stack. Call this right = -0.6. Pop the top number from the operand stack. Call this left = 1. Pop the top operator from the operator stack. Call this operator =*. Evaluate operator and push the result (-0.6) onto the operand stack. 17. The operator stack is empty. Pop the result from the operand stack (-0.6) and return it. 4 Software Requirements The project shall implement a GUI calculator which accepts as input a syntactically correct arithmetic expression written in infix notation and displays the result of evaluating the expression. The program shall meet these requirements. 1. The program shall implement a GUI which permits the user to interact with the calculator. Watch the Project 4 video lecture for a demonstration of how the application works. 2. When the Clear button is clicked, the input text field and the result label shall be configured to display nothing. 3. When a syntactically correct infix arithmetic expression is entered in the input text field and the Evaluate button is clicked, the program shall evaluate the expression and display the result in the label of the GUI. 4. When the input text field is empty, clicking the Evaluate button does nothing. 5. When the Exit button is clicked, the application shall terminate. 6. Note: you do not have to be concerned with syntactically incorrect infix expressions. We will not test your program with such expressions. 5 Software Design Refer to the UML class diagram in Section 5.21. Your program shall implement this design 5.1 Main Class The Main class shall contain the main() method which shall instantiate an object of the Main class and call rund) on that > ce205-p04.pdf X 0 O fe///C:/Users/dow12/AppData/local/temp/Temp ce205-pol.zip/cse205-poc/doc/c2205-p04.pdf 5.1 Main Class The Main class shall contain the main() method which shall instantiate an object of the Main class and call run() on that object. Main is completed for you. 5.2 AddOperator Implements the addition operator, which is a binary operator. AddOperator is completed for you. Use AddOperator as a guide when completing DivOperator, MultOperator, and SubOperator. 5.3 BinaryOperator The abstract superclass of all binary operators. BinaryOperator is completed for you. Note that BinaryOperator imple- ments one abstract method evaluate() which all subclasses must implement. The subclasses are AddOperator, DivOperator, MultOperator, and Sub Operator. 5.4 DivOperator Implements the division operator, which is a binary operator. Complete the code in this file by using the AddOperator class as an example. 5.5 DList This is the DList class from the Module 7 Source Code zip archive. It implements a generic doubly linked list where the data type of each list element is E. DList is completed for you. For example, to create a DList which stores elements of the type Token you would write DList list - new DList>0; much in the same way that we can create an ArrayList of Doubles by writing ArrayList list = new ArrayList(); 5.6 Expression Represents an infix expression to be evaluated. Use the provided pseudocode as a guide in completing this class. ce205-p04.pdf 0 > file:///C:/Users/dow12/AppData/local/Temp/Temp 1 cse205-p04.zip/cse205-p04/doc/cse205-p04.pdf 5.7 LeftParen Represents a left parenthesis in the expression. LeftParen is completed for you. Note that Left Paren is a subclass of the abstract class Parenthesis. 5.8 MultOperator Implements the multiplication operator, which is a binary operator. Complete the code in this file by using the AddOperat- or class as an example. 5.9 NegOperator Implements the negation operator, which is a unary operator. Complete the code in this file by using the AddOperator class as an example. Note, however, that negation is a unary operator so it only has one operand. 5.10 Operand An operand is a numeric value represented as a Double. Implement the class using the UML class diagram as a guide. 5.11 Operator Operator is the abstract superclass of all binary and unary operators, ie, it is the superclass of BinaryOperator and UnaryOperator. Implement the class using the UML class diagram as a guide. Note that all of the non-constructor methods are abstract, ie, none of them are implemented in Operator. 5.12 Parenthesis Parenthesis is the superclass of Left Paren and Right Paren. These are treated as a weird sort of Operator because we need to be able to push Left Parens on the operator stack when evaluating the expression. Parenthesis is completed for you. 5.13 Queue Implements a generic queue data structure using a DList list to store the elements. This is the same class that was 5.12 Parenthesis Parenthesis is the superclass of LeftParen and Right Paren. These are treated as a weird sort of Operator because we need to be able to push LeftParens on the operator stack when evaluating the expression. Parenthesis is completed for you. 5.13 Queue Implements a generic queue data structure using a DList list to store the elements. This is the same class that was provided in the Week 7 Source zip archive. Queue is completed for you. 5.14 Right Paren Represents a right parenthesis in the expression. RightParen is completed for you. 5.15 Stack Implements a generic stack data structure using a DList list to store the elements. This is the same class that was provided in the Module 7 Source zip archive. Stack is completed for you. 5.16 SubOperator Implements the subtraction operator, which is a binary operator. Complete the code in this file by using the AddOperator class as an example, 5.17 Token Token is the abstract superclass of the different types of tokens (ie., symbols) that can appear in an infix expression. Token is completed for you. 5.18 Tokenizer The Tokenizer class scans a String containing an infix expression and breaks it into tokens. For this project, a token will be either an Operand (a double value), a Left Paren or Right Paren, or an arithmetic UnaryOperator (subclass Neg Operator or BinaryOperator (one of the AddOperator, SubOperator MultOperator or DivOperator subclasses) Tokenizer is com 0 0 file:///C:/Users/dow 12/AppData/local/temp/Temp1 cse205-po4.zip/cse205-pol/doc/cse205-p04.pdf Emprenem a gente queue LA BUCURE provided in the Week 7 Source zip archive. Queue is completed for you. 5.14 RightParen Represents a right parenthesis in the expression. Right Paren is completed for you. 5.15 Stack Implements a generic stack data structure using a DList list to store the elements. This is the same class that was provided in the Module 7 Source zip archive. Stack is completed for you. 5.16 SubOperator Implements the subtraction operator, which is a binary operator. Complete the code in this file by using the AddOperator class as an example 5.17 Token Token is the abstract superclass of the different types of tokens (1.e., symbols) that can appear in an infix expression Token is completed for you. 5.18 Tokenizer The Tokenizer class scans a String containing an infix expression and breaks it into tokens. For this project, a token will be either an Operand (a double value), a LeftParen or Right Paren, or an arithmetic UnaryOperator (subclass Neg Operator) or BinaryOperator (one of the AddOperator, SubOperator MultOperator, or DivOperator subclasses). Tokenizer is com- pleted for you. It is implemented as a finite state machine (FSM) which are commonly used in computing, especially when breaking a "sentence" of words or symbols into its component parts. If you have the time, you should study the code to learn how FSM's work and are used. - MEM E /doc/c5e205-p04.pdf 5.19 UnaryOperator UnaryOperator is the superclass of all unary operators. UnaryOperator is completed for you. 5.20 View The View implements the GUI. Read the comments and implement the pseudocode. 5.21 UML Class Diagram The UML class diagram is provided in the zip archive uml folder as two UMLet files. Because the images in this document are small, there are PNG images of the two class diagrams in the image folder. Your program shall implement this design. Token +Token actory Operator . Operand mValue: Double +Operand(pValue: Double actor + getValue: Double setValue(pValue Double): void +Operator): -ctor + BinaryOperator:boolean + precedence: int +stackPrecedenceint AA Parenthesis - 15 Binary Operator boolean UnaryOperator +Unary Operator: -ctor- evaluate Operand: 0 perand: Operand + is BinaryOperator: boolean Binary Operator Binary Operator) -ctor auteurs perand: Operand properand Opera Biopero boolean Operand Left Paren -LetParent ectora. + precedencent stack Precedenceint l lesOperator Negoperator) actor -evaluate pOperand: Operand Operand precedence int AddOperator Adsoperatorio w h o perand: Operand phsoperand Opera dencent Operand Right Paren 11:22 AM this design. Token Token: ector Operand mValue Double +Operand(pvalue: Doubles actor +getValue(): Double setValue(pValue Double): void Operator +Operator: actor +is BinaryOperator: boolean precedence: int + stack Precedence: int UnaryOperator Unary Operator: ector + evaluate(pOperand: 0 perand: Operand isBinaryOperator) boolean Parenthesis Parenthesistor +iBinaryOperator> boolean 04 Binary Operator +Binary Operator): -ctor + evaluate(puh perand: Operandphsoperando perand. Operand + is BinaryOperator) boolean AAAA teft Paren +Left Paren stor + precedence(): int + stack Precedence in NegOperator NegOperator: actor -evaluate pOperand: Operand): Operand precedence: int stack Precedence in AddOperator + Addoperator): -ctor + evaluatepths perand: Operand. AhsOperand Operand) Operand precedenceint stack Precedenceint Richteren Right Parent to precedenceint stackPrecedent DivOperator -ctor + evaluateplhs perand. Operand phsOperand Operand) Operand + precedenceint + stackPrecedenceint MultOperator + MultOperator: { 17e * For a nonempty DList, mHead is a reference to the first Node in the DList. For an empty 19 * DList, mHead will be null. 2e */ private Node mhead; * The number of Nodes containing data in this Dist. For an empty DList mize is 0. - private int Size; * For a nonempty Dlist mail is a reference to the last Node in the Dist. For an empty Dlist, * mail will be null. * private Node m Tail; 35 * Creates an empty Dist. For an empty DList, mHead = null, mail = null, and mSize - e. 37 39 public DList() { setHead(null); setTail(null); setSize(); 40 41 432 Creates a new DList with one element containing pData. 45 public DList() { setHead(null); setTail(null); setSize(); 39 40 41 42 43e 44 45 46e * Creates a new DList with one element containing pData. */ public DList(E pData) { // Create a new Node storing pData. Make the mPrev and mNext references null. Node newNode = new Node(pData); 47 // Make the mHead reference refer to the new node. setHead (rewNode); 7/ Make the mTail reference refer to the new node. setTail(newNode); // The size of the list is now 1. setSize(1); 600 * Inserts a new Node containing pData into this DList at index pIndex. Shifts the element * currently at that index (if it exists) and succeeding elements to the right (i.e., adds one * to their indices). * Note that if pIndex -- getSize() then new element is appended to the list. Throws an IndexOutOfBounds Exception if pIndex size of the DList. public void add(int pIndex, EpData) throws IndexOutOfBoundsException 17 Check for pIndex out of bounds. if (pIndex getSize() throw new IndexOutOfBounds Exception(); // Are we appending? if nlnderot 59e public void add(int pIndex, EpData) throws IndexOutOfBoundsException { 1/ Check for pIndex out of bounds. if (pIndex getSize() throw new IndexOutOfBoundsException(); 11 Are we appending? if (pIndex = getSize()) { // Create a new Node storing pData. The mNext reference is initialized to null because 1/ the new Node will become the tail Node of the DList and the mNext reference of the // tail Node is always null. The mPrev reference is initialized to mail so it will 1/ refer to the Node preceding the new Node. Node newNode = new Node(pData, getTail(), null); // If this list is empty the new Node becomes the head Node. Otherwise change mNext of // the tail Node to refer to the new Node. if (IsEmpty()) setHead(newNode); else getTail().setNext(newNode); // In any case, we must change mTail to refer to the new Node that is now at the tail. setTail(newNode); // We are not appending. else { 1/ Get a reference to the Node at pIndex. We are inserting a new Node before 'node'. Node node = getNodeAt(pIndex); // Create a new Node storing pData. Set the mPrev reference of the new Node to refer to // the Node preceding "node'. Set the mNext reference of the new Node to refer to 1/ 'node Node newNode = new Node(pData, node.getPrev(), node); // If we are not inserting at pindex = @ then we need to change the mNext reference of Listjava X Unary Operatorjaa View.java J Expression.java Queue.java Stack.java SubOperator.java Token.java Tokenizer java else { // Get a reference to the Node at pIndex. We are inserting a new Node before 'node'. Node node = getNodeAt (pIndex); // Create a new Node storing pData. Set the mPrev reference of the new Node to refer to // the Node preceding 'node'. Set the mNext reference of the new Node to refer to // 'node Node newNode = new Node(pData, node.getPrev(), node); // If we are not inserting at pIndex = @ then we need to change the mNext reference of // the Node preceding 'node' to refer to the new Node. if (pIndex ! - ) node.getPrev().setNext(newNode); // Make the mPrev reference of 'node' refer to the new Node. The result of these three // operations is to "link" the the new Node into the DList. node.setPrev(newNode); 107 108 109 // Are we inserting at index e? If so, we need to change the head to refer to the new 7/ Node because the new Node is now at head if (pIndex == 0) setHead(newNode); 110 111 112 114 // We have added a new Node to the Dist. Increment the size of the list. setSize(getSize() + 1); 116 117 * Appends a new Node storing pData to this list. Note that passing an index of getSize() to * add(int pIndex, EpData) will cause add() to perform an append operation. 119 12e public void append(E pData) { add(getSize(), pData); 121- 122 123 124 125- 126 123 * Removes all of the elements from the Dist. After this operation the list will be empty. Tan bocomar 108 199 110 // Are we inserting at index @? If so, we need to change the head to refer to the new // Node because the new Node is now at head. if (pIndex - 0) setHead(newNode); 114 // We have added a new Node to the DList. Increment the size of the list. setSize(getSize() + 1); * Appends a new Node storing pData to this DList. Note that passing an index of getSize() to * add(int pIndex, E pData) will cause */ public void append(E pData) { add(getSize(), pData); 119 120 121 122 123 124 125 126 127 128- 129 130 131 132 * Removes all of the elements from the Dlist. After this operation the DList will be empty. public void clear() { // To clear the list is simple. Simply remove the node at index @ until the list becomes // empty. while (!isEmpty()) { remove(); } 134 public DList clone() { DList clonelist = new DList(); Node traverse - getHead(); while (traverse != null) { cloneList.append(traverse.getData()); traverse - traverse.getNext(); return clonelist; * Removes all of the elements from the Dist. After this operation the DList will be empty. 126 127 1280 129 130 131 132 public void clear() { // To clear the list is simple. Simply remove the node at index until the list becomes // empty. while (!isEmpty()) { remove(); } 133 1346 135 136 137 138 public DList clone() { DList cloneList = new DList(); Node traverse = getHead(); while (traverse != null) { cloneList.append(traverse.getData()); traverse = traverse.getNext(); 139 140 141 return cloneList; 142 143 1440 145 146 * Returns the element at index pIndex. 147 - Thows IndexOutOfBounds Exception if pIndex = mSize. 148 149- 150 public E get(int pIndex) throws IndexOutOfBounds exception return getNodeAt (pIndex).getData(); 151 152 153- 154 * Accessor method for the mead field. 155 protected Node getHead() { return mHead; 156 157 158 159 150 - 161 162 Returns a reference to the Node at index pIndex. - Returns a reference to the Node at index pIndex. 650 Thows IndexOutOfBoundsException if pIndex = getSize() */ protected Node getNodeAt(int pIndex) throws IndexOutOfBoundsException { 1/ Check for pIndex out of bounds and throw exception is necessary. if (pIndex = getSize() throw new IndexOutOfBoundsException(); 66 67 168 169 170 173 1/ Since accessing the head and tail nodes is a common operation we check for those cases // first. if (pIndex == ) return getHead(); else if (pIndex - getSize() - 1) return getTail(); // Otherwise, start at the node at index 1 and walk forward until the node at index pIndex 7/ is reached and then return it. Node node = getHead().getNext(); for (int index = 1; index getTail() { return Tail; ist.java > Expression java Queue.java Stack.java SubOperator.java Tokenjava Tokenizer.java UnaryOperator.java View.java * Accessor method for the mail field, */ protected Node getTail() { return mTail; } e /** * Returns true if this DList is empty. public boolean isEmpty() { return getSize() == 0; - Prepends new Node storing pData to this list. 5 public void prepend(E pData) { addo, pData); 29- SHA Removes the element at index pIndex from this Dist. Shifts any succeeding elements to the left (i.e., subtracts one from their indices). Returns the element that was removed from * the list. Throws an IndexOutOfBounds Exception is pIndex node = getNodeAt (pIndex); 7/ Are we removing the only element in a list with one element? if (getSize() == 1) { setHead(null); setTail(null); 220 221 TIPOLL - - 215 2160 217 218 219 public E remove(int pIndex) throws IndexOutOfBoundsException { Node node - getNodeAt (pIndex); 1/ Are we removing the only element in a list with one element? if (getSize() -- 1) { setHead(null); setTail(null); 17 Else are we removing the head node in a list with more than one element (note: we will // not get here if the list has only one element)? else if (pIndex == ) { 1/ Change the prev reference of the next node to null because the next node will now 17 bd the head node in the list. node.getNext().setPrev(null); // Since we removed the head node, we have to change the head reference to refer to the 17 next node succeeding the one that was just removed. setHead (node.getNext(); // Else are we removing the tail node in a list with more than one element note we will 71 not get here if the list has only one element)? else if (pIndex == getSize()-1){ 1/ Change the next reference of the previous node to null because the previous node will 17 now be the tail node in the list. node.getPrev().setNext(null); 242 Since we removed the tail node, we have to change the tail reference to refer to the 11 previous node preceding the one that was just removed setTail(node.getPrev()); 247 We are not removing the head or tall node else node.getPrev().settlext(node.getNext()); node.getliext().setPrev(node.getPrev()); Read-Only Smart Insert 1:1:0 210M of 497M 11 we are not removing the redu ur dit noue. else { node.getPrev().setNext(node.getNext()); node.getNext().setPrev(node.getPrev()); HNNNNNN // We have removed a Node so decrement the size of the list. setSize(getSize() - 1); 7/ Return the data stored at the removed Node. return node.getData(); 258 259 260 261 2620 263 264 265 266 Replaces the element at the specified position in this list with the specified element. - Returns the element that was previously stored at pIndex. 267 public E set(int pIndex, E pData) throws IndexOutOfBoundsException { Node node = getNodeAt (pIndex); E original = node.getData(); node.setData(pData); return original; / * Mutator method for the mHead field. * 268 269 270 271 272 2736 274 275 276 277 278 279 280- 281 282 283- protected void setHead (Node pHead) { mHead = pHead; Mutator method for the mize field. protected void setSize(int psize) { mSize = pSize; 285 Stack.java SubOperator.java J Token.java Tokenizer.java UnaryOperator java View.java DListjava > Expression.java Queue.java 282 */ 2830 protected void setSize(int pSize) { 284 mSize = pSize; 285 } 286 2876 288 * Mutator method for the mail field. 289 2900 protected void setTail(Node pTail) { 291 mTail pTail; 292 */ 293 * Returns a string representation of this list where we define string representation be the string representation of each of the Nodes. 2949 295 296 297 298 299 300 301 302 Be 304 305 306 @Override public String toString() { String string = ""; int i; for (i = 0; i mTokenQueue; Expression(String) * pExprstr is a string representing an infix expression, such as "(1 + 2)"-3". This ctor uses the *Tokenizer class to break the string into Token objects which are stored in the token queue instance * variable. * PSEUDOCODE: * Create a new Queue object and pass it to setTokenQueue (this initializes mTokenQueue) * Declare and create a Tokenizer object named tokenizer passing pExprstr to the ctor Declare a Token object named prevToken initialized to null -- Read the first token Declare a Token object named token and assign the return value from tokenizer.nextToken() to it -- Keep reading tokens until tokenizer.nextToken() returns null while token is not null Do -- Check for and handle the negation operator. If token instanceof SubOperator Then token - negationCheck(token, prevToken) End if - Add the token to the queue. Call getTokenQueue().enqueue (token) prevToken = token - Read the next token. token - call tokenizer.nextToken() End While ??? Read-Only Smart Insert 1:1:0 245M of 497M * Evaluates the expression and returns the result as a Double. * PSEUDOCODE: * Declare and create a Stack object named operatorStack Declare and create a Stack object named operandStack While mTokenQueue is not empty Do Declare and create a Token object named token assigning getTokenQueue().dequeue() to it If token instanceof Operand Then Push token onto the operand stack (type cast token to Operand) ElseIf token instanceof LeftParen Then Push token onto the operator stack (type cast token to LeftParen) ElseIf token instanceof RightParen Then while the operator on the top of the operator stack is not an instanceof LeftParen Do Call topEval(operatorStack, operandStack) End while Pop the top operator from the operator stack -- removes the LeftParen Else Declare Operator object named operator and assign token to it (type cast to Operator) While keepEvaluating (operatorStack, operator) is true Do Call topEval(operatorStack, operandStack) Endwhile Push operator onto the operator stack End If * End while While the operator stack is not empty Do * Call topEval(operatorStack, operandStack) End While Pop the top Operand from the operand stack and return its value (call getValue() on the Operand). ??? 82- 83 Accessor method for mTokenQueue. 85 - 86 protected Queue getTokenQueue() { return mTokenQueue; 85e 86 protected Queue getTokenQueue() { return mTokenQueue; 38 89e Returns true when we need to pop the operator on top of the operator stack and evaluate it. If the stack is empty, returns false since there is no operator to pop. Otherwise, return true if the operator on top * of the operator stack has stack precedence greater than or equal to the normal precedence of poperator. . 95 96 private boolean keepEvaluating(Stack pOperatorStack, Operator pOperator) { if (pOperatorStack.isEmpty()) { return false; } else { return pOperatorStack.peek().stackPrecedence() >= pOperator.precedence(); 98 00 32- 03 " Since the negation and subtraction operators look the same we can identify negation when: 25 36 * 1. The previous pToken is null (negation can be the first operator in an expression but sub cannot) 2. Or if the previous pToken was a binary operator (sub cannot be preceded by another binary operator) * 3. Or if the previous pToken was a left parenthesis (sub cannot be preceded by a left paren) * This method determines if proken is really a negation operator rather than a subtraction operator, and if 50, will return a negation operator proken. If poken represents subtraction, then we simply return pToken. private Token negationCheck(Token pToken, Token pPrevToken) { if (pPrevToken == null || pPrevToken instanceof BinaryOperator || pPrevToken instanceof LeftParen) { pToken = new NegOperator(); return pToken; Mutator method for nTokenQueue. * Mutator method for mTokenQueue. */ protected void setTokenQueue (Queue pTokenQueue) { mTokenQueue = pTokenQueue; topEval() * Evaluates the "top" of the stack. If the top operator on the operator stack is a unary operator, we pop one operand from the operand stack, evaluate the result, and push the result onto the operand stack. If the top operator on the operator stack is a binary operator, we pop two operands from the operand stack, evaluate the result of the operation, and push the result onto the operand stack. DoWNOW PSEUDOCODE: * Declare and create Operand object named right = Call pOperandStack.pop() * Declare and create Operator object named operator = Call pOperatorStack.pop() * If operator instanceof UnaryOperator Then Typecast operator to UnaryOperator and call evaluate(right) on it Push the returned Operand from the above statement onto the operand stack Else Declare and create Operand object named left - Call pOperandStack.pop() Typecast operator to BinaryOperator and call evaluate(left, right) on it Push the returned Operand from the above statement onto the operand stack * End If ??? Read-Only Smart Insert 1:1:0 256M View.java 17 18 U O JU TULI .Java Unayoperator.java 12 130 /** 14 Implements a generic queue data structure using a DList to store the elements. 15 */ 16 public class Queue { private DList mList; 19 200 * Creates a new empty Queue by creating a new empty DList. 23 public Queue () { setlist(new DList ); 25 } 26 270 / * Removes all of the elements from this Queue. After clear() returns this Queue is empty. /** 21 22 */ 24 300 public void clear() { getList().clear(); 33 35 Removes and returns the element that is at the front of this Queue. 36 public E dequeue() { E front = getList().remove(); return front; 42- 43 Adds pData to the rear of this Queue. 45 public void enqueue (E pData) { getList().append(pData); 45e public void enqueue (E pData) { getList().append(pData); 46 48 490 * Accessor method for mList. 5e 51 +/ 52e protected DList getList() { return mList; 53 54 569 57 - Returns true if this Queue is empty. 58 598 60 61 62 636 public boolean isEmpty() { return getList().isEmpty(); * Returns the front element of this Queue without removing it. 65 66- public E peek() { return getList().get(); 68 69 70- 71 72 735 74 * Mutator method for mlist. protected void setlist(DList plist) { mList = plist; 76 77e 78 * Overrides toString() inherited from Object. Returns a String representation of the elements of this Queue by calling the list.toString() method. RA 58 59e 60 61 public boolean isEmpty() { return getList().isEmpty(); 62 63e 64 65 * Returns the front element of this Queue without removing it. 660 public E peek() { return getList().get(); 67 68 69 700 * Mutator method for mList. */ 72 730 74 75 protected void setlist(DList plist) { mList = pList; } 776 * Overrides toString() inherited from Object. Returns a String representation of the elements * of this Queue by calling the DList.toString method. 79 * 810 00 00 DO @Override public String toString() { return getList().toString(); Smart Insert Read-Only 1:1:0 View.java Stack.java x SubOperator.java Token.java Tokenizer.java U naryOperator.java 130 /** 14 * Implements a generic stack data structure using a Dlist to store the elements. 15 */ 16 public class Stack { private DList mList; 19 20e * Creates a new empty Stack by creating a new empty Dlist. * 22 */ 23e public Stack() { setList(new DList(); 26 270 * Removes all of the elements from this Stack. After clear() returns this Stack is empty. * 29 300 public void clear() { getList().clear(); 32 34 * Accessor method for mist. */ protected DList getList() { return mList; 37- *Returns true if this Stack is empty. ws public boolean isEmpty() { return getList().isEmpty(); } os 43 440 45 public boolean isEmpty() { return getList().isEmpty(); 46 47 489 ** 49 * Returns the top element on this Stack without removing it. 50 510 52 53 54 public E peek() { return getList().get(); 55e 56 * Removes the top element from this Stack and returns it. public E pop() { E top = getList().remove(); return top; } I 60 61 62 632 64 65 66- 67 68 1 * Pushes pData onto the top of this Stack. public void push(E pData) { getList() .prepend(pData); 69 71 Mutator method for mlist. 73 protected void setlist(DList plist) { mList - pList; 77- 78 Overrides toString() inherited from object. Returns a String representation of the elements of this Stack by calling the list.toString() method. @Override public E pop() { E top = getList().remove(); return top: 61 630 64 * Pushes pData onto the top of this Stack. */ public void push(E pData) {I getList()-prepend (pData); 66- 68 69 700 71 72 * Mutator method for mList. 730 74 75 protected void setlist(DList plist) { mList = plist; 76 77e 78 79 80 * Overrides toString() inherited from Object. Returns a String representation of the elements * of this Stack by calling the DList.toString() method. @Override public String toString() { return getList().to