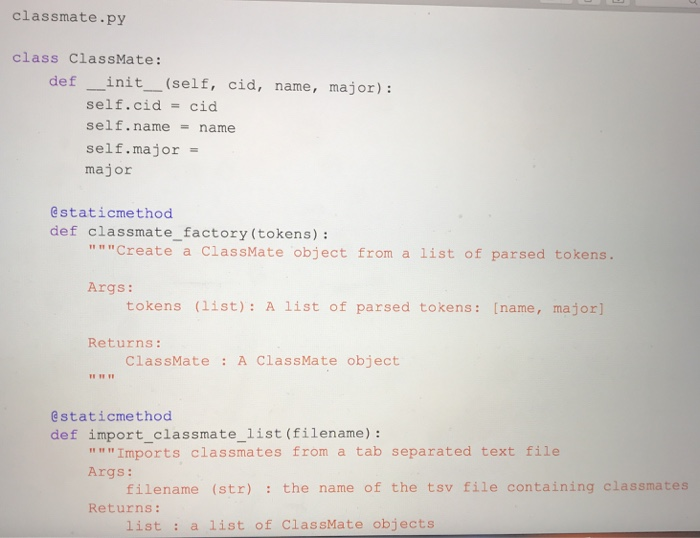
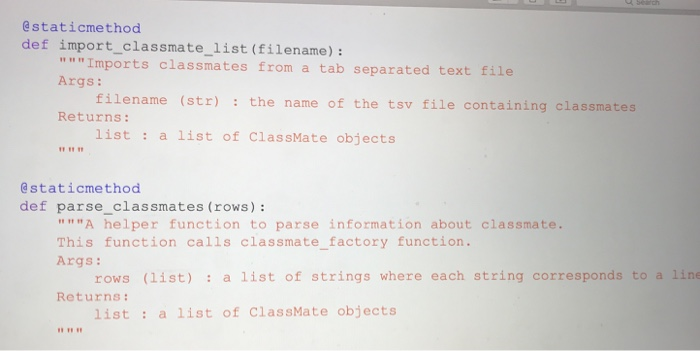
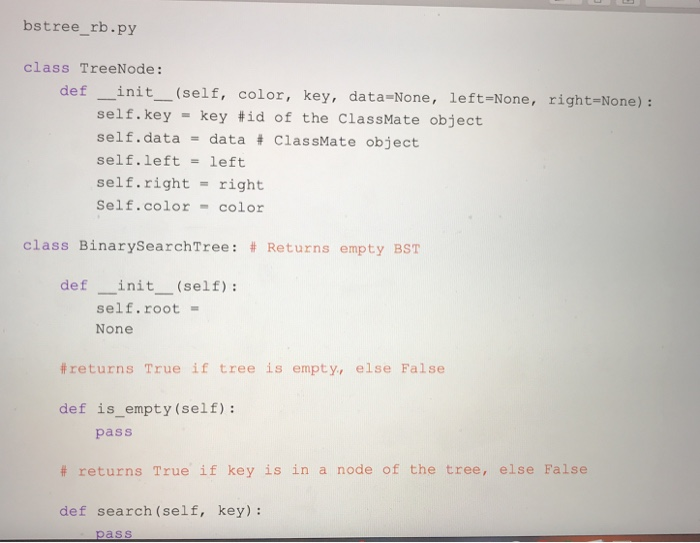
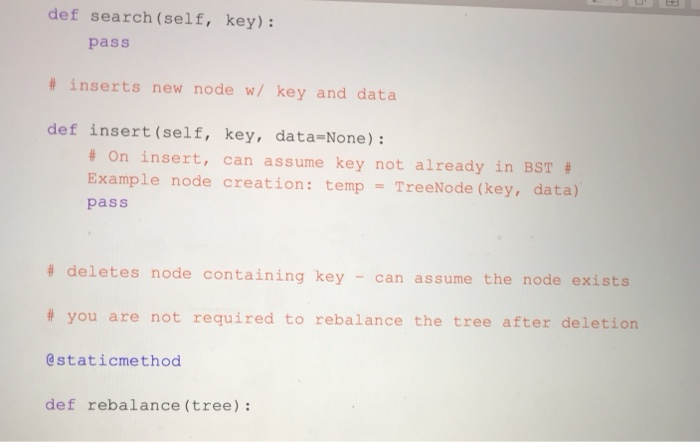
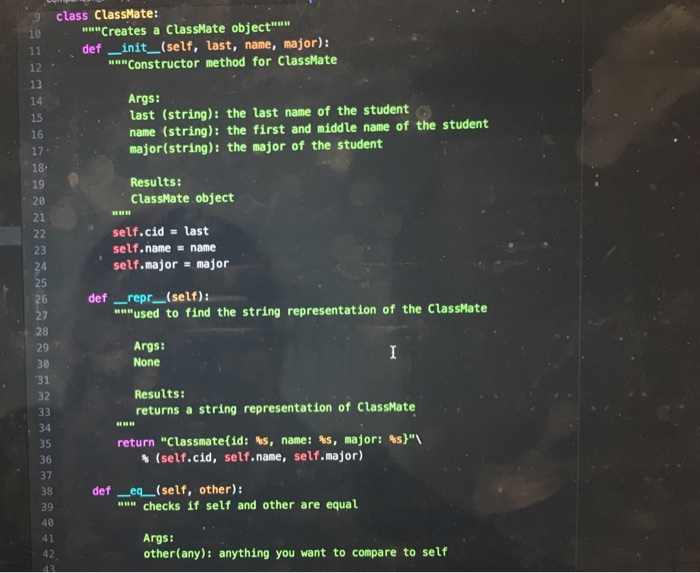
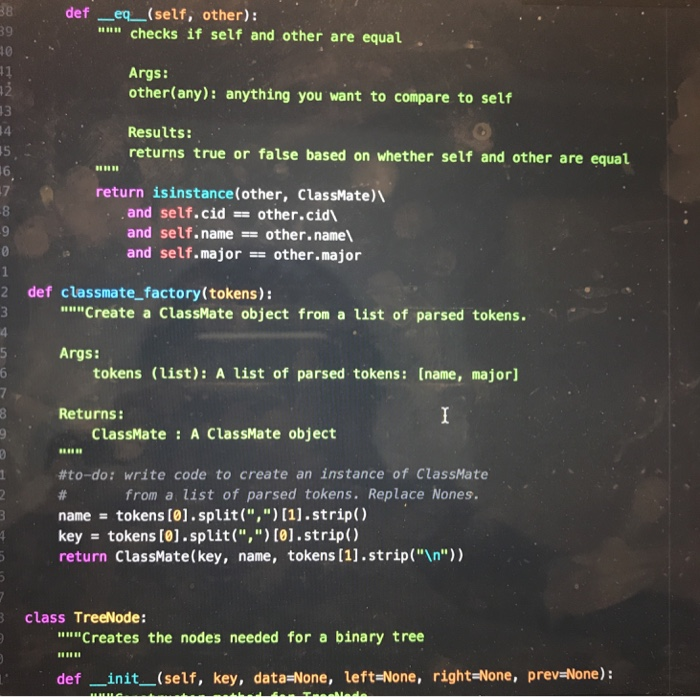
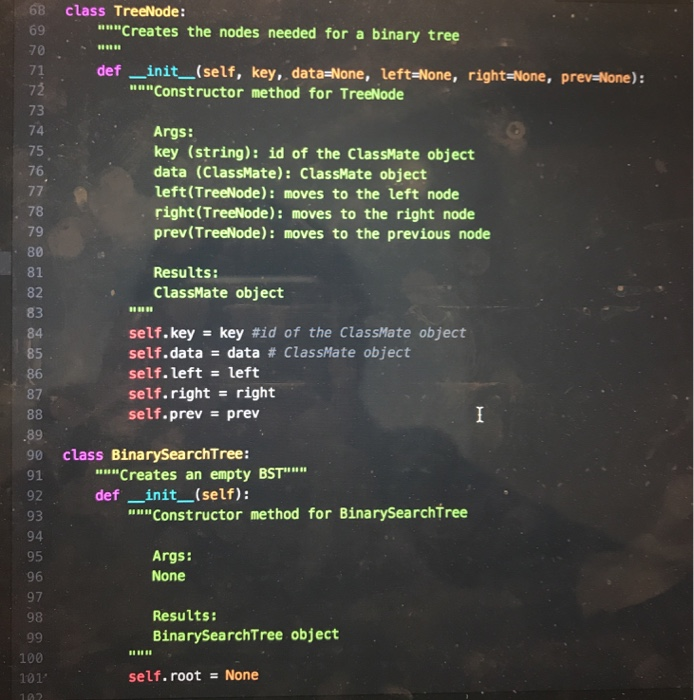
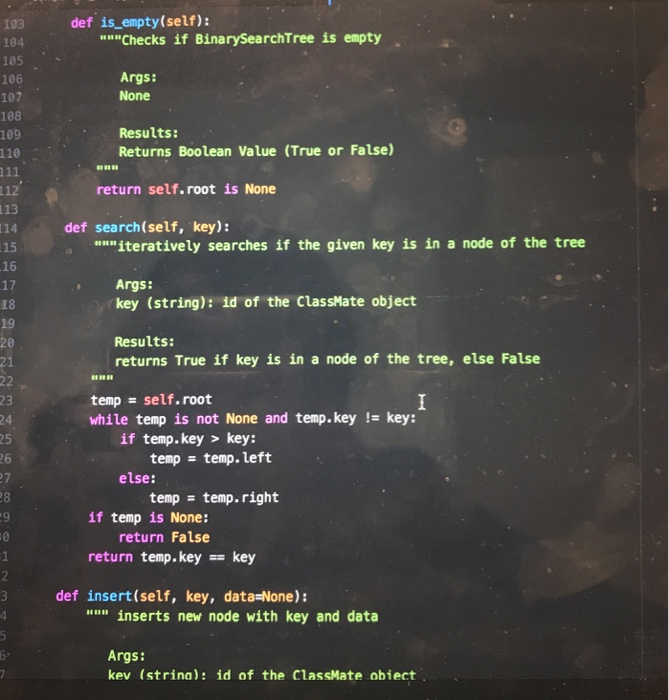
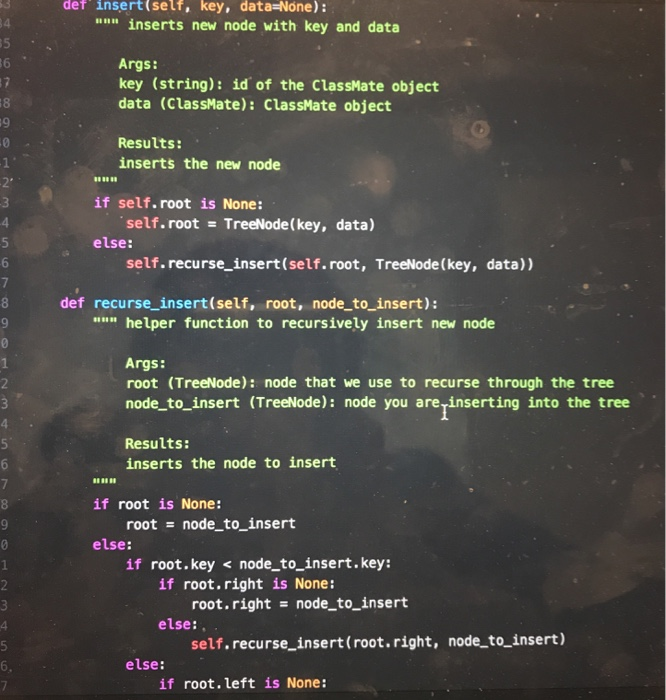
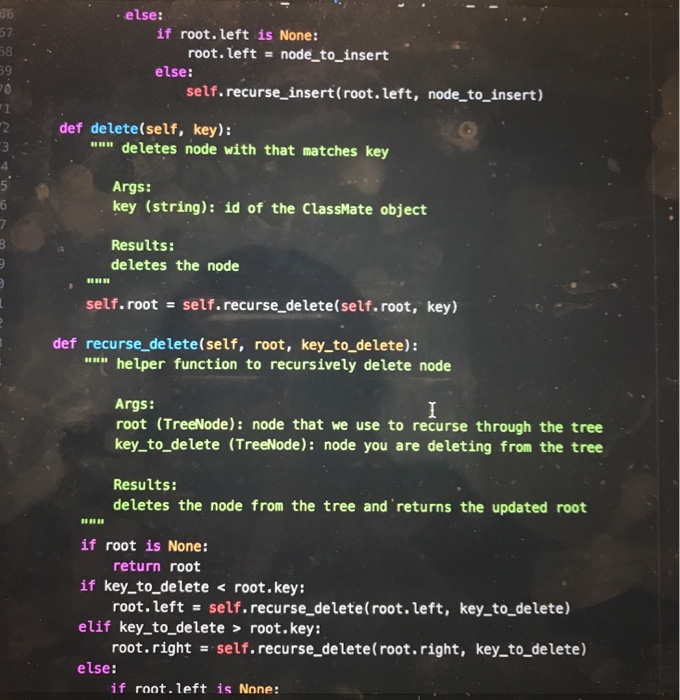
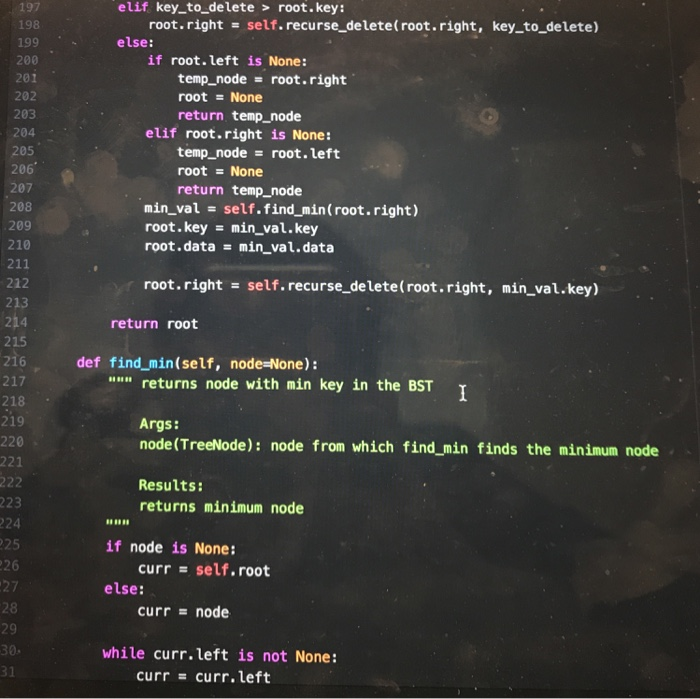
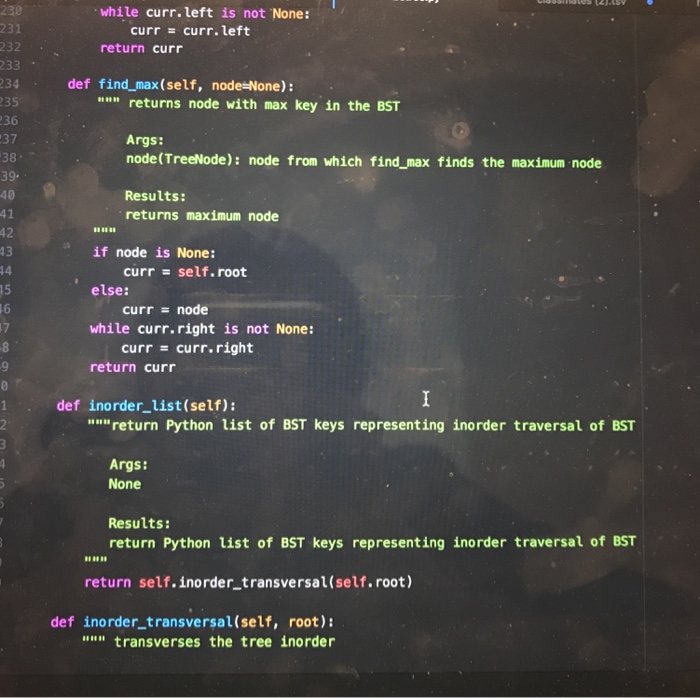
Question: need some help completing this lab 10 as soon as possible! the code in black is from a previous lab that i did that this
need some help completing this lab 10 as soon as possible!
the code in black is from a previous lab that i did that this one is a continuation of.
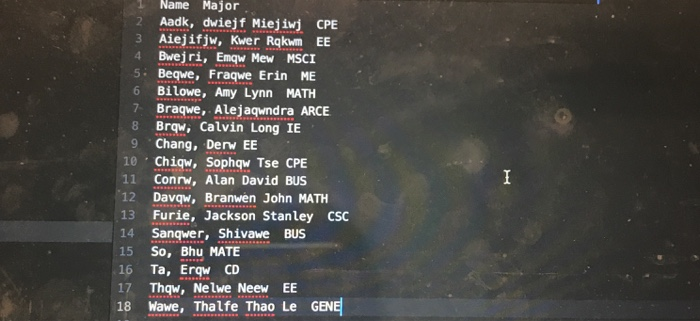
the file with student names is one that i created and is needed for this lab.
thanks!

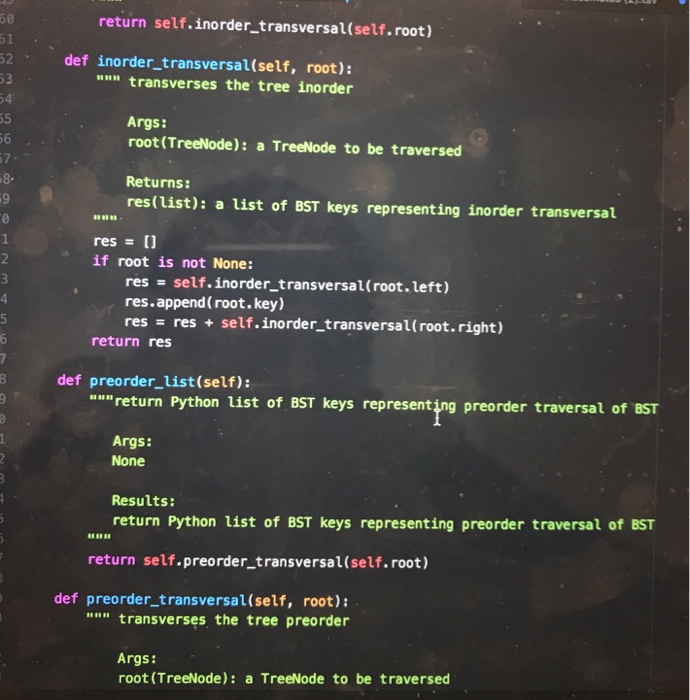
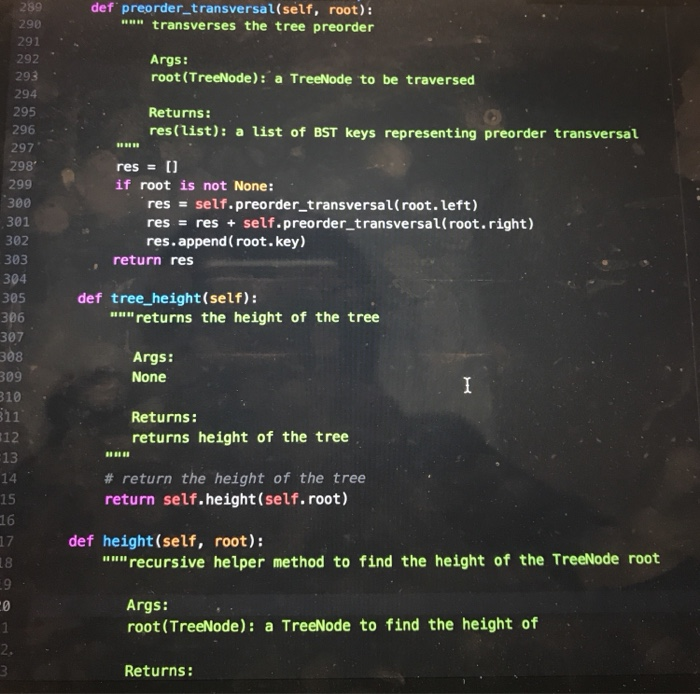
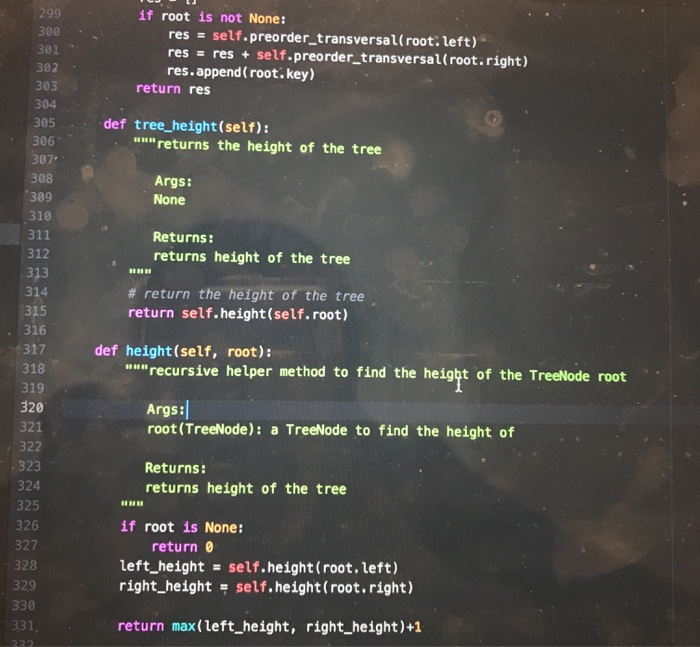
CPE202 Winter 2019 Lab10: Red Black Tree Due: demo your work by 10 am Friday March 15th BinarySearchTrees (BSTs) are great. They allow us to organize and search for items in O(log(n)) time rather than O(n) time, and to insert things in O(log(n) time as well. However, a binary search tree can devolve into a simple linear list, if the elements are inserted in sequential order. In that case, the time complexity of using BST becomes O(n). Therefore, BST needs to be balanced. There are a number of different ways of balancing BST. Two of the most well-known are AVL trees and Red-Black trees. Of the two, red-black trees are slightly newer, have more reliable insertion times, and are a bit simpler to implement for us. (Note: We need to relax the definition of a balanced tree to consider Red-Black trees to be balanced.) The properties of a Red-Black tree are: 1. 2. Each node is labeled as either "red" or "black." Root is always black a. This rule is relaxed in some implementations. Every path from root to leaf encounters the exact same number of black nodes. The child of a red node must be a black node. In other words, there can't be more than one red node in a row along a path from root to leaf 3. 4. a. NIL (None) leaves are considered black. 3. 4. Every path from root to leaf encounters the exact same number of black nodes. The child of a red node must be a black node. In other words, there can't be more than one red node in a row along a path from root to leaf. a. NIL (None) leaves are considered black. In this lab, you are going to implement a self-balancing BST using the red-black tree. 1. Create a file "bstree_rb.py' and implement Binary Search Tree as you did in Lab 5 (You can reuse your program from lab 5). 2. Add a str field "color" in TreeNode class for red black tree. 3. Add a method "rebalance" in BinarySearch Tree class for red black tree. 4. Modify the insert method or its helper function/method in the BinarySearchTree class to rebalance the tree if the red black tree property is violated. For example, add a static method "rebalance" as shown below. Create a file "classmate.py" and add a static method "classmate_factory" in the ClassMate class (move the existing classmate_factory inside the class). Add a static method "import_classmate_ list" which takes a tsv filename including its path as an argument and returns a list of classmate objects in the ClassMate class. The file contains tab separated text data of classmates in this class. Download the classmates.tsv from polylearn if you do not have it. You may want to add helper functions/methods to parse information about classmates from the file as shown below. 5. 6. 7. Create a file called "lab 10." and add a function (not a class method) "build-tree" which takes a list of classmate objects as an argument and creates a BinarySearch Tree object and insert each classmate object in the list into the tree and returns the BinarySearchTree object. We no longer shuffle the list of classmates because the red black tree is supposed to rebalance itself. 8. Create a test file "lab10_test.py" and write tests for the methods in BinarySearchTree 9. Visualized images of expected binary search tree of classmates are available on 10. OPTIONAL EXTRA CREDIT ASSIGNMENT (extra 10 points in lab category and 10 class as well as the build-tree function in lab10. polylearn. points in project category): create a function to visual representation of the binary search tree using graphviz as shown in lecture and create image (png) files of binary search trees of classmates. The function need to output a text description of the tree in the dot language to a file. Then you can use "dot" command to create a png file from the text description: dot out.dot -Tpng-o out.png, where out.dot is an output file generated by your program and out.png is an image file name and both filenames are for you to choose freely. The "dot" command is available on the unix server on campus. You can find the documentation about graphviz here: https://graphviz.gitlab.iol https://renenyffenegger.chotes/tools/Graphvizlexamples/index ldps.flcodeyams.com/2013/06/24/how-to-conven dat ile to-image-fornat 11. Zip all files into one file and submit it to polylearn. classmate.py class ClassMate: def init_ _(self, cid, name, major): self.cd = cid self.namename self.major major @staticmethod def classmate_factory (tokens): m"Create a ClassMate object from a list of parsed tokens. Args: tokens (list): A list of parsed tokens: [name, major] Returns: ClassMate A ClassMate object @staticmethod def import_classmate_list (filename): """Imports classmates from a tab separated text file Args: filename (str) the name of the tsv file containing classmates Returns: list a list of ClassMate objects estaticmethod def import_classmate_list (filename): ""Imports classmates from a tab separated text Args: filename (str) the name of the tsv file containing classmates list a list of ClassMate objects Returns: @staticmethod def parse_classmates (rows): """A helper function to parse information about classmate. This function calls classmate factory function. Args: rows (list) a list of strings where each string corresponds to a lire Returns: list a list of ClassMate objects bstree_rb.py class TreeNode: def -init _(self, color, key, data-None, left-None, right-None) self.key key #id of the ClassMate object self.data = data # ClassMate object self. left left self.right right Self.color color class BinarySearchTree : # Returns empty BST def init (self): self.root - None #re turns True if tree is empty, else False def is_empty(self): pass # returns True if key is in a node of the tree, else False def search(self, key) : def search (self, key): pass # inserts new node w/ key and data def insert (self, key, data-None) # on insert, can assume key not already in BST Example node creation: temp TreeNode (key, data) pass # deletes node containing key-can assume the node exists # you are not required to rebalance the tree after deletion @staticmethod def rebalance (tree): m"Rebalance the tree so that the property of the RB Tree is maintained. If the subtree matches one of the 4 patters, it will convert the subtree to Args: tree (TreeNode): a Float Red Black Tree Returns: TreeNode a Float Red Black Tree lef delete (self, key): # will need to consider all cases - will likely want helper functions # like findsuccessor() and splice-out() pass - def delete (self, key): # will need to consider all cases - will likely want helper functions # like find-successor() and splice-out () pass # returns node with min key in the BST-can assume at least one node in BST def find_min(self): pass # returns node with max key in the BST - can assume at least one node in BST def find max (self): pass # return Python list of BST keys representing inorder traversal of BST def inorder list (self): pass # return Python list of BST keys representing preorder traversal of BST def preorder_list (self) pass # return the height of the tree def tree_ height (self) pass class ClassMate: """Creates a ClassMate object"" def init (self, last, name, major): Constructor method for ClassMate 12 13 last (string): the last name of the student name (string): the first and middle name of the student major(string): the major of the student 15 16 17 18 19 20 21 Results: ClassMate object self.cid last self.name name self.major major 24 25 def _repr (self): ""used to find the string representation of the ClassMate 28 29 30 31 32 Args: None Results: returns a string representation of ClassMate %s, major: %s)"\ ts, self.major) return "Classmate( id: name: 35 36 37 % (self.cid, self.name, 38 def _eq (self, other): 39 40 41 42 wn" checks if self and other are equal Args: other(any): anything you want to compare to self 38 def eq (self, other): checks if self and other are equal. Args: other(any): anything you want to compare to self 13 ,4 Results: returns true or false based on whether self and other are equal 5 6 7 return isinstance(other, ClassMate) and self.cid : other.cia and self.name other.name and self.major other.major 2 def classmate factory(tokens): ""Create a ClassMate object from a list of parsed tokens Args: tokens (list): A list of parsed tokens: (name, major] Returns: ClassMate A ClassMate object #to-do: write code to create an instance of ClassMate from a list of parsed tokens. Replace Nones. name tokens [0l.split (",") (11.strip) key tokens [0].split(",")(e].strip() return ClassMate(key, name, tokens [1].strip("In")) class TreeNode: """Creates the nodes needed for a binary tree def _init_(self, key, data None, left None, right-None, prev-None): 68 class TreeNode: 69 70 Creates the nodes needed for a binary tree 71 def init_(self, key, data-None, left-None, right -None, prev-None): Constructor method for TreeNode 73 74 75 76 Args: key (string): id of the ClassMate object data (ClassMate): ClassMate object left(TreeNode): moves to the left node right (TreeNode): moves to the right node prev(TreeNode): moves to the previous node 78 79 80 81 Results: ClassMate object 83 84 85 86 self.key key #id of the ClassMate object self.data data # ClassMate object self.left left self.right- right self.prevprev 89 90 class BinarySearchTree: 91 92 93 94 95 96 97 98 """Creates an empty BST"" def init_ (self): """Constructor method for BinarySearchTree Args: None Results: BinarySearchTree object 100 101 self.root None def is_empty(self): 103 104 105 106 107 108 109 110 "Checks if BinarySearchTree is empty Args: None Results: Returns Boolean Value (True or False) 112 return self.root is None 113 def search(self, key): 114 15 16 17 18 19 ""iteratively searches if the given key is in a node of the tree Args: key (string): id of the ClassMate object Results: returns True if key is in a node of the tree, else False 23 24 temp self.root while temp is not None and temp.key !# key: if temp.key >key: 26 temp temp. left else: temp temp. right 28 .9 0 if temp is None: return False return temp.keykey def insert(self, key, data None): inserts new node with key and data Args: kev (strina): id of the ClassMate obiect def insert self, key, data-None): uu" inserts new node with key and data 5 6 Args: key (string): id of the ClassMate object data (ClassMate): ClassMate object 9 Results: inserts the new node if self.root is None: self.root TreeNode(key, data) else: 6 self.recurse_insert(self.root, TreeNode(key, data)) 8 def recurse insert(self, root, node to_insert): "n" helper function to recursively insert new node Args: root (TreeNode): node that we use to recurse through the tree node to_insert (TreeNode): node you arerinserting into the tree 4 Results: inserts the node to insert if root is None: root node_to_insert else: if root.keyroot.key: else: return root root left = self.recurse_delete (root. Ieft, key-to-delete) root.right- self.recurse_delete(root.right, key_to_delete) if root.left is None: 197 198 199 200 elif key_to delete> root.key: root.right self.recurse_delete(root.right, key_to_delete) else: if root.left is None: 201 202 203 204 205 206 07 208 209 210 211 212 213 temp_node root.right rootNone return temp_node elif root.right is None: temp_node-root.left root None return temp_node min val self.find_min(root.right) root.key min_ val.key root.datamin val.data root.right-self.recurse_delete ( root.right, min val.key) return root 215 216 def find_min(self, node-None): "" returns node with min key in the BST 217 218 219 220 221 Args: node(TreeNode): node from which find_min finds the minimum node Results: returns minimum node 223 224 225 if node is None: 26 curr self. root 27 28 29 30- 31 else: curr node while curr.left is not None: curr curr.left while curr. left is not None: 231 curr curr.left 232 return curr 233 def find_max(self, node-None): 234 235 236 nun returns node with max key in the BST Args: node(TreeNode): node from which find_max finds the maximum node 38 39- 40 41 42 43 Results: returns maximum node if node is None: curr self.root else: while curr.right is not None: return curr 6 7 curr node curr curr.right 1def inorder list(self): """return Python list of BST keys representing inorder traversal of BST Args: None Results: return Python list of BST keys representing inorder traversal of BST return self.inorder_transversal(self.root) def inorder transversal(self, root): "transverses the tree inorder return self.inorder_transversal(self.root) 51 def inorder_transversal(self, root): uu transverses the tree inorder Args: root(TreeNode): a TreeNode to be traversed 6 8- 9 Returns: res(list): a list of BST keys representing inorder transversal 8 res[ if root is not None: res - self.inorder_transversal(root.left) res.append ( root.key) res res+ self.inorder transversaL( root.right) return res def preorder_list(self): wa return Python list of BST keys representing preorder traversal of BST Args: None Results: return Python list of BST keys representing preorder traversal of BST return self.preorder_transversal(self.root) def preorder_transversal(self, root) """ transverses the tree preorder Args: root (TreeNode): a TreeNode to be traversed 289 290 291 292 293 294 def preorder transversal(self, root): """ transverses the tree preorder Args: root (TreeNode): a TreeNode to be traversed 295 296 297 298 299 300 301 302 303 304 Returns: res(list): a list of BST keys representing preorder transversal res[ if root is not None: res -self.preorder_transversal(root.left) res = res + self.preorder_transversal(root.right) res.append (root.key) return res def tree height(self): 305 306 307 """returns the height of the tree Args: None 309 310 1 Returns: returns height of the tree 13 # return the height of the tree return self.height(self.root) 15 16 def height(self, root): recursive helper method to find the height of the TreeNode root 18 9 0 Args: root (TreeNode): a TreeNode to find the height of Returns: if root is not None: 300 301 302 res self.preorder_transversal(root: left) res = res + self.preorder_transversal(root.right) res.append (root.key) 30 return res 304 305 306 307- 308 def tree_height(self): "s" returns the height of the tree Args: None 309 310 311 312 313 314 Returns: returns height of the tree # return the height of the tree return self.height(self.root) 316 317 318 319 320 321 322 def height(self, root): uu"recursive helper method to find the height of the TreeNode root Args: root (TreeNode): a TreeNode to find the height of 323 324 325 326 327 328 329 330 331 Returns: returns height of the tree un if root is None: return 0 left_height self.height (root. left) right_height self.height (root.right) return max(left_height, right height)+1 Name Major Aadk, dwiejf Miejiwj CPE 3 Aiejifjw, Kwer Rgkwm EE 4 Bwejri, Emqw Mew MSCI 5 Beqwe, Fraqwe Erin ME 6 Bilowe, Amy Lynn MATH 7 Braqwe, Alejaqwndra ARCE 8 Brqw, Calvin Long IE 9Chang, Derw EE 10 Chiqw, Sophqw Tse CPE 11 Conrw, Alan David BUS 12 Davqw, Branwen John MATH 13 Furie, Jackson Stanley CSC 14 Sanqwer, Shivawe BUS 15 So, Bhu MATE 16 Ta, Erqw CD 17 Thqw, Nelwe Neew EE 18 Wave, Thalfe Thao Le GENE CPE202 Winter 2019 Lab10: Red Black Tree Due: demo your work by 10 am Friday March 15th BinarySearchTrees (BSTs) are great. They allow us to organize and search for items in O(log(n)) time rather than O(n) time, and to insert things in O(log(n) time as well. However, a binary search tree can devolve into a simple linear list, if the elements are inserted in sequential order. In that case, the time complexity of using BST becomes O(n). Therefore, BST needs to be balanced. There are a number of different ways of balancing BST. Two of the most well-known are AVL trees and Red-Black trees. Of the two, red-black trees are slightly newer, have more reliable insertion times, and are a bit simpler to implement for us. (Note: We need to relax the definition of a balanced tree to consider Red-Black trees to be balanced.) The properties of a Red-Black tree are: 1. 2. Each node is labeled as either "red" or "black." Root is always black a. This rule is relaxed in some implementations. Every path from root to leaf encounters the exact same number of black nodes. The child of a red node must be a black node. In other words, there can't be more than one red node in a row along a path from root to leaf 3. 4. a. NIL (None) leaves are considered black. 3. 4. Every path from root to leaf encounters the exact same number of black nodes. The child of a red node must be a black node. In other words, there can't be more than one red node in a row along a path from root to leaf. a. NIL (None) leaves are considered black. In this lab, you are going to implement a self-balancing BST using the red-black tree. 1. Create a file "bstree_rb.py' and implement Binary Search Tree as you did in Lab 5 (You can reuse your program from lab 5). 2. Add a str field "color" in TreeNode class for red black tree. 3. Add a method "rebalance" in BinarySearch Tree class for red black tree. 4. Modify the insert method or its helper function/method in the BinarySearchTree class to rebalance the tree if the red black tree property is violated. For example, add a static method "rebalance" as shown below. Create a file "classmate.py" and add a static method "classmate_factory" in the ClassMate class (move the existing classmate_factory inside the class). Add a static method "import_classmate_ list" which takes a tsv filename including its path as an argument and returns a list of classmate objects in the ClassMate class. The file contains tab separated text data of classmates in this class. Download the classmates.tsv from polylearn if you do not have it. You may want to add helper functions/methods to parse information about classmates from the file as shown below. 5. 6. 7. Create a file called "lab 10." and add a function (not a class method) "build-tree" which takes a list of classmate objects as an argument and creates a BinarySearch Tree object and insert each classmate object in the list into the tree and returns the BinarySearchTree object. We no longer shuffle the list of classmates because the red black tree is supposed to rebalance itself. 8. Create a test file "lab10_test.py" and write tests for the methods in BinarySearchTree 9. Visualized images of expected binary search tree of classmates are available on 10. OPTIONAL EXTRA CREDIT ASSIGNMENT (extra 10 points in lab category and 10 class as well as the build-tree function in lab10. polylearn. points in project category): create a function to visual representation of the binary search tree using graphviz as shown in lecture and create image (png) files of binary search trees of classmates. The function need to output a text description of the tree in the dot language to a file. Then you can use "dot" command to create a png file from the text description: dot out.dot -Tpng-o out.png, where out.dot is an output file generated by your program and out.png is an image file name and both filenames are for you to choose freely. The "dot" command is available on the unix server on campus. You can find the documentation about graphviz here: https://graphviz.gitlab.iol https://renenyffenegger.chotes/tools/Graphvizlexamples/index ldps.flcodeyams.com/2013/06/24/how-to-conven dat ile to-image-fornat 11. Zip all files into one file and submit it to polylearn. classmate.py class ClassMate: def init_ _(self, cid, name, major): self.cd = cid self.namename self.major major @staticmethod def classmate_factory (tokens): m"Create a ClassMate object from a list of parsed tokens. Args: tokens (list): A list of parsed tokens: [name, major] Returns: ClassMate A ClassMate object @staticmethod def import_classmate_list (filename): """Imports classmates from a tab separated text file Args: filename (str) the name of the tsv file containing classmates Returns: list a list of ClassMate objects estaticmethod def import_classmate_list (filename): ""Imports classmates from a tab separated text Args: filename (str) the name of the tsv file containing classmates list a list of ClassMate objects Returns: @staticmethod def parse_classmates (rows): """A helper function to parse information about classmate. This function calls classmate factory function. Args: rows (list) a list of strings where each string corresponds to a lire Returns: list a list of ClassMate objects bstree_rb.py class TreeNode: def -init _(self, color, key, data-None, left-None, right-None) self.key key #id of the ClassMate object self.data = data # ClassMate object self. left left self.right right Self.color color class BinarySearchTree : # Returns empty BST def init (self): self.root - None #re turns True if tree is empty, else False def is_empty(self): pass # returns True if key is in a node of the tree, else False def search(self, key) : def search (self, key): pass # inserts new node w/ key and data def insert (self, key, data-None) # on insert, can assume key not already in BST Example node creation: temp TreeNode (key, data) pass # deletes node containing key-can assume the node exists # you are not required to rebalance the tree after deletion @staticmethod def rebalance (tree): m"Rebalance the tree so that the property of the RB Tree is maintained. If the subtree matches one of the 4 patters, it will convert the subtree to Args: tree (TreeNode): a Float Red Black Tree Returns: TreeNode a Float Red Black Tree lef delete (self, key): # will need to consider all cases - will likely want helper functions # like findsuccessor() and splice-out() pass - def delete (self, key): # will need to consider all cases - will likely want helper functions # like find-successor() and splice-out () pass # returns node with min key in the BST-can assume at least one node in BST def find_min(self): pass # returns node with max key in the BST - can assume at least one node in BST def find max (self): pass # return Python list of BST keys representing inorder traversal of BST def inorder list (self): pass # return Python list of BST keys representing preorder traversal of BST def preorder_list (self) pass # return the height of the tree def tree_ height (self) pass class ClassMate: """Creates a ClassMate object"" def init (self, last, name, major): Constructor method for ClassMate 12 13 last (string): the last name of the student name (string): the first and middle name of the student major(string): the major of the student 15 16 17 18 19 20 21 Results: ClassMate object self.cid last self.name name self.major major 24 25 def _repr (self): ""used to find the string representation of the ClassMate 28 29 30 31 32 Args: None Results: returns a string representation of ClassMate %s, major: %s)"\ ts, self.major) return "Classmate( id: name: 35 36 37 % (self.cid, self.name, 38 def _eq (self, other): 39 40 41 42 wn" checks if self and other are equal Args: other(any): anything you want to compare to self 38 def eq (self, other): checks if self and other are equal. Args: other(any): anything you want to compare to self 13 ,4 Results: returns true or false based on whether self and other are equal 5 6 7 return isinstance(other, ClassMate) and self.cid : other.cia and self.name other.name and self.major other.major 2 def classmate factory(tokens): ""Create a ClassMate object from a list of parsed tokens Args: tokens (list): A list of parsed tokens: (name, major] Returns: ClassMate A ClassMate object #to-do: write code to create an instance of ClassMate from a list of parsed tokens. Replace Nones. name tokens [0l.split (",") (11.strip) key tokens [0].split(",")(e].strip() return ClassMate(key, name, tokens [1].strip("In")) class TreeNode: """Creates the nodes needed for a binary tree def _init_(self, key, data None, left None, right-None, prev-None): 68 class TreeNode: 69 70 Creates the nodes needed for a binary tree 71 def init_(self, key, data-None, left-None, right -None, prev-None): Constructor method for TreeNode 73 74 75 76 Args: key (string): id of the ClassMate object data (ClassMate): ClassMate object left(TreeNode): moves to the left node right (TreeNode): moves to the right node prev(TreeNode): moves to the previous node 78 79 80 81 Results: ClassMate object 83 84 85 86 self.key key #id of the ClassMate object self.data data # ClassMate object self.left left self.right- right self.prevprev 89 90 class BinarySearchTree: 91 92 93 94 95 96 97 98 """Creates an empty BST"" def init_ (self): """Constructor method for BinarySearchTree Args: None Results: BinarySearchTree object 100 101 self.root None def is_empty(self): 103 104 105 106 107 108 109 110 "Checks if BinarySearchTree is empty Args: None Results: Returns Boolean Value (True or False) 112 return self.root is None 113 def search(self, key): 114 15 16 17 18 19 ""iteratively searches if the given key is in a node of the tree Args: key (string): id of the ClassMate object Results: returns True if key is in a node of the tree, else False 23 24 temp self.root while temp is not None and temp.key !# key: if temp.key >key: 26 temp temp. left else: temp temp. right 28 .9 0 if temp is None: return False return temp.keykey def insert(self, key, data None): inserts new node with key and data Args: kev (strina): id of the ClassMate obiect def insert self, key, data-None): uu" inserts new node with key and data 5 6 Args: key (string): id of the ClassMate object data (ClassMate): ClassMate object 9 Results: inserts the new node if self.root is None: self.root TreeNode(key, data) else: 6 self.recurse_insert(self.root, TreeNode(key, data)) 8 def recurse insert(self, root, node to_insert): "n" helper function to recursively insert new node Args: root (TreeNode): node that we use to recurse through the tree node to_insert (TreeNode): node you arerinserting into the tree 4 Results: inserts the node to insert if root is None: root node_to_insert else: if root.keyroot.key: else: return root root left = self.recurse_delete (root. Ieft, key-to-delete) root.right- self.recurse_delete(root.right, key_to_delete) if root.left is None: 197 198 199 200 elif key_to delete> root.key: root.right self.recurse_delete(root.right, key_to_delete) else: if root.left is None: 201 202 203 204 205 206 07 208 209 210 211 212 213 temp_node root.right rootNone return temp_node elif root.right is None: temp_node-root.left root None return temp_node min val self.find_min(root.right) root.key min_ val.key root.datamin val.data root.right-self.recurse_delete ( root.right, min val.key) return root 215 216 def find_min(self, node-None): "" returns node with min key in the BST 217 218 219 220 221 Args: node(TreeNode): node from which find_min finds the minimum node Results: returns minimum node 223 224 225 if node is None: 26 curr self. root 27 28 29 30- 31 else: curr node while curr.left is not None: curr curr.left while curr. left is not None: 231 curr curr.left 232 return curr 233 def find_max(self, node-None): 234 235 236 nun returns node with max key in the BST Args: node(TreeNode): node from which find_max finds the maximum node 38 39- 40 41 42 43 Results: returns maximum node if node is None: curr self.root else: while curr.right is not None: return curr 6 7 curr node curr curr.right 1def inorder list(self): """return Python list of BST keys representing inorder traversal of BST Args: None Results: return Python list of BST keys representing inorder traversal of BST return self.inorder_transversal(self.root) def inorder transversal(self, root): "transverses the tree inorder return self.inorder_transversal(self.root) 51 def inorder_transversal(self, root): uu transverses the tree inorder Args: root(TreeNode): a TreeNode to be traversed 6 8- 9 Returns: res(list): a list of BST keys representing inorder transversal 8 res[ if root is not None: res - self.inorder_transversal(root.left) res.append ( root.key) res res+ self.inorder transversaL( root.right) return res def preorder_list(self): wa return Python list of BST keys representing preorder traversal of BST Args: None Results: return Python list of BST keys representing preorder traversal of BST return self.preorder_transversal(self.root) def preorder_transversal(self, root) """ transverses the tree preorder Args: root (TreeNode): a TreeNode to be traversed 289 290 291 292 293 294 def preorder transversal(self, root): """ transverses the tree preorder Args: root (TreeNode): a TreeNode to be traversed 295 296 297 298 299 300 301 302 303 304 Returns: res(list): a list of BST keys representing preorder transversal res[ if root is not None: res -self.preorder_transversal(root.left) res = res + self.preorder_transversal(root.right) res.append (root.key) return res def tree height(self): 305 306 307 """returns the height of the tree Args: None 309 310 1 Returns: returns height of the tree 13 # return the height of the tree return self.height(self.root) 15 16 def height(self, root): recursive helper method to find the height of the TreeNode root 18 9 0 Args: root (TreeNode): a TreeNode to find the height of Returns: if root is not None: 300 301 302 res self.preorder_transversal(root: left) res = res + self.preorder_transversal(root.right) res.append (root.key) 30 return res 304 305 306 307- 308 def tree_height(self): "s" returns the height of the tree Args: None 309 310 311 312 313 314 Returns: returns height of the tree # return the height of the tree return self.height(self.root) 316 317 318 319 320 321 322 def height(self, root): uu"recursive helper method to find the height of the TreeNode root Args: root (TreeNode): a TreeNode to find the height of 323 324 325 326 327 328 329 330 331 Returns: returns height of the tree un if root is None: return 0 left_height self.height (root. left) right_height self.height (root.right) return max(left_height, right height)+1 Name Major Aadk, dwiejf Miejiwj CPE 3 Aiejifjw, Kwer Rgkwm EE 4 Bwejri, Emqw Mew MSCI 5 Beqwe, Fraqwe Erin ME 6 Bilowe, Amy Lynn MATH 7 Braqwe, Alejaqwndra ARCE 8 Brqw, Calvin Long IE 9Chang, Derw EE 10 Chiqw, Sophqw Tse CPE 11 Conrw, Alan David BUS 12 Davqw, Branwen John MATH 13 Furie, Jackson Stanley CSC 14 Sanqwer, Shivawe BUS 15 So, Bhu MATE 16 Ta, Erqw CD 17 Thqw, Nelwe Neew EE 18 Wave, Thalfe Thao Le GENE